《2020版高考物理大一輪復(fù)習(xí) 第四章 基礎(chǔ)課3 圓周運動訓(xùn)練（含解析）教科版》由會員分享，可在線閱讀，更多相關(guān)《2020版高考物理大一輪復(fù)習(xí) 第四章 基礎(chǔ)課3 圓周運動訓(xùn)練（含解析）教科版（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

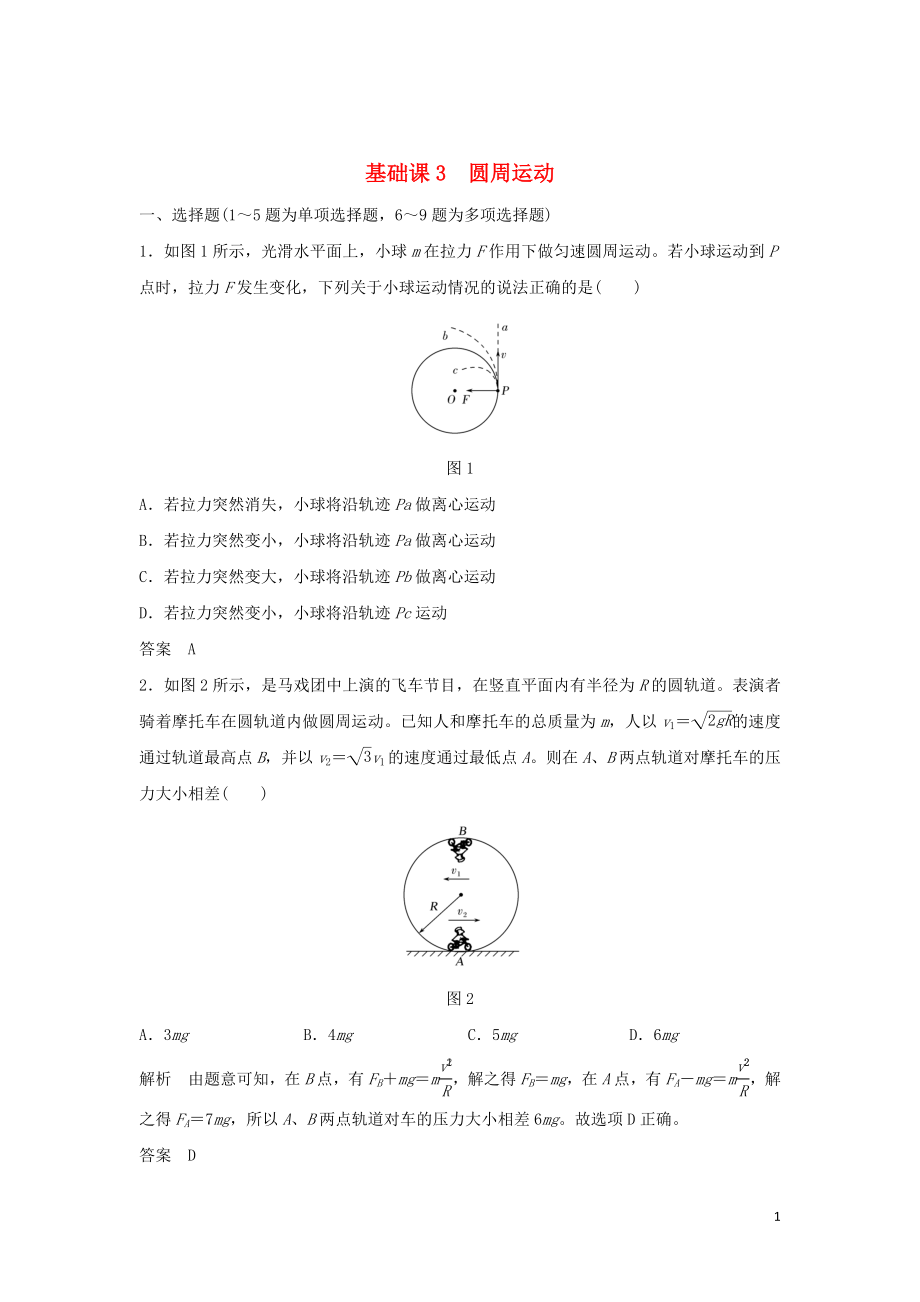
1、基礎(chǔ)課3　圓周運動 一、選擇題(1～5題為單項選擇題，6～9題為多項選擇題) 1．如圖1所示，光滑水平面上，小球m在拉力F作用下做勻速圓周運動。若小球運動到P點時，拉力F發(fā)生變化，下列關(guān)于小球運動情況的說法正確的是(　　) 圖1 A．若拉力突然消失，小球?qū)⒀剀壽EPa做離心運動 B．若拉力突然變小，小球?qū)⒀剀壽EPa做離心運動 C．若拉力突然變大，小球?qū)⒀剀壽EPb做離心運動 D．若拉力突然變小，小球?qū)⒀剀壽EPc運動 答案　A 2．如圖2所示，是馬戲團(tuán)中上演的飛車節(jié)目，在豎直平面內(nèi)有半徑為R的圓軌道。表演者騎著摩托車在圓軌道內(nèi)做圓周運動。已知人和摩托車的總質(zhì)量為m，人以v1＝的

2、速度通過軌道最高點B，并以v2＝v1的速度通過最低點A。則在A、B兩點軌道對摩托車的壓力大小相差(　　) 圖2 A．3mg B．4mg C．5mg D．6mg 解析　由題意可知，在B點，有FB＋mg＝m，解之得FB＝mg，在A點，有FA－mg＝m，解之得FA＝7mg，所以A、B兩點軌道對車的壓力大小相差6mg。故選項D正確。 答案　D 3．如圖3所示，小物體P放在水平圓盤上隨圓盤一起轉(zhuǎn)動，下列關(guān)于小物體所受摩擦力f的敘述正確的是(　　) 圖3 A．f的方向總是指向圓心 B．圓盤勻速轉(zhuǎn)動時f＝0 C．在物體與軸O的距離一定的條件下，f跟圓盤轉(zhuǎn)動的角速度成正比

3、D．在轉(zhuǎn)速一定的條件下，f跟物體到軸O的距離成正比 解析　物體隨圓盤轉(zhuǎn)動過程中，如果圓盤勻速轉(zhuǎn)動，則摩擦力指向圓心，如果變速轉(zhuǎn)動，則摩擦力的一個分力充當(dāng)向心力，另一個分力產(chǎn)生切向加速度，摩擦力不指向圓心，A、B錯誤；根據(jù)公式F＝f＝mω2r可得在物體與軸O的距離一定的條件下，f跟圓盤轉(zhuǎn)動的角速度的平方成正比，C錯誤；因為ω＝2πn，所以f＝m(2πn)2r，則f跟物體到軸O的距離成正比，D正確。 答案　D 4．(2017·宜賓市調(diào)研)質(zhì)量為m的物體隨水平傳送帶一起勻速運動，A為傳送帶的終端皮帶輪。如圖4所示，皮帶輪半徑為r，要使物體通過終端時能水平拋出，皮帶輪的轉(zhuǎn)速至少為(　　)

4、圖4 A. 　　　　B. C. 　　　　D. 解析　要使物體通過終端時能水平拋出，則有mg＝，物體飛出時速度至少為，由v＝ωr＝2πnr可得皮帶輪的轉(zhuǎn)速至少為n＝，選項A正確。 答案　A 5．如圖5所示，轉(zhuǎn)動軸垂直于光滑平面，交點O的上方h處固定細(xì)繩的一端，細(xì)繩的另一端拴接一質(zhì)量為m的小球B，繩長AB＝l＞h，小球可隨轉(zhuǎn)動軸轉(zhuǎn)動并在光滑水平面上做勻速圓周運動。要使球不離開水平面，轉(zhuǎn)動軸的轉(zhuǎn)速的最大值是(　　) 圖5 A. B．π C. D．2π 解析　對小球，在水平方向有Tsin θ＝mω2R＝4π2mn2R，在豎直方向有Tcos θ＋N＝mg，且R＝htan θ

5、＝lsin θ，當(dāng)球即將離開水平面時，N＝0，轉(zhuǎn)速n有最大值，聯(lián)立解得n＝＝，則A正確。 答案　A 6．鐵路轉(zhuǎn)彎處的彎道半徑r是根據(jù)地形決定的。彎道處要求外軌比內(nèi)軌高，其內(nèi)、外軌高度差h的設(shè)計不僅與r有關(guān)。還與火車在彎道上的行駛速度v有關(guān)。下列說法正確的是(　　) A．速率v一定時，r越小，要求h越大 B．速率v一定時，r越大，要求h越大 C．半徑r一定時，v越小，要求h越大 D．半徑r一定時，v越大，要求h越大 解析　火車轉(zhuǎn)彎時，圓周平面在水平面內(nèi)，火車以設(shè)計速率行駛時，向心力剛好由重力G與軌道支持力N的合力來提供，如圖所示，則有mgtan θ＝，且tan θ≈sin θ＝

6、，其中L為軌間距，是定值，有mg＝，通過分析可知A、D正確。 答案　AD 7．如圖6所示，質(zhì)量為m的物體，沿著半徑為R的半球形金屬殼內(nèi)壁滑下，半球形金屬殼豎直固定放置，開口向上，滑到最低點時速度大小為v，若物體與球殼之間的動摩擦因數(shù)為μ，則物體在最低點時，下列說法正確的是(　　) 圖6 A．受到的向心力為mg＋m B．受到的摩擦力為μm C．受到的摩擦力為μ(mg＋m) D．受到的合力方向斜向左上方 解析　物體在最低點做圓周運動，則有N－mg＝m，解得N＝mg＋m，故物體受到的滑動摩擦力f＝μN(yùn)＝μ(mg＋m)，A、B錯誤，C正確；物體受到豎直向下的重力、水平向左的摩擦

7、力和豎直向上的支持力(支持力大于重力)，故物體所受的合力斜向左上方，D正確。 答案　CD 8．(2016·宜昌聯(lián)考)如圖7所示，半徑為R的光滑細(xì)圓環(huán)軌道被固定在豎直平面上，軌道正上方和正下方分別有質(zhì)量為2m和m的靜止小球A、B，它們由長為2R的輕桿固定連接，圓環(huán)軌道內(nèi)壁開有環(huán)形小槽，可使細(xì)桿無摩擦、無障礙地繞其中心點轉(zhuǎn)動。今對上方小球A施加微小擾動。兩球開始運動后，下列說法正確的是(　　) 圖7 A．輕桿轉(zhuǎn)到水平位置時兩球的加速度大小相等 B．輕桿轉(zhuǎn)到豎直位置時兩球的加速度大小不相等 C．運動過程中A球速度的最大值為 D．當(dāng)A球運動到最低點時，兩小球?qū)壍雷饔昧Φ暮狭Υ笮閙

8、g 解析　兩球做圓周運動，在任意位置角速度相等，則線速度和向心加速度大小相等，選項A正確，B錯誤；A、B球組成的系統(tǒng)機(jī)械能守恒，當(dāng)系統(tǒng)重力勢能最小(即A為最低點)時，線速度最大，則mg·2R＝·3mv2，最大速度v＝，選項C正確；A在最低點時，分別對A、B受力分析，NA－2mg＝2m，NB＋mg＝m，則NA－NB＝，選項D正確。 答案　ACD 9．如圖8所示，一個固定在豎直平面上的光滑半圓形管道，管道里有一個直徑略小于管道內(nèi)徑的小球，小球在管道內(nèi)做圓周運動，從B點脫離后做平拋運動，經(jīng)過0.3 s后又恰好垂直與傾角為45°的斜面相碰。已知半圓形管道的半徑R＝1 m，小球可看做質(zhì)點且其質(zhì)量為

9、m＝1 kg，g取10 m/s2。則(　　) 圖8 A．小球在斜面上的相碰點C與B點的水平距離是0.9 m B．小球在斜面上的相碰點C與B點的水平距離是1.9 m C．小球經(jīng)過管道的B點時，受到管道的作用力FNB的大小是1 N D．小球經(jīng)過管道的B點時，受到管道的作用力FNB的大小是2 N 解析　根據(jù)平拋運動的規(guī)律，小球在C點的豎直分速度vy＝gt＝3 m/s，水平分速度vx＝vytan 45°＝3 m/s，則B點與C點的水平距離為x＝vxt＝0.9 m，選項A正確，B錯誤；在B點設(shè)管道對小球的作用力方向向下，根據(jù)牛頓第二定律，有NB＋mg＝m，vB＝vx＝3 m/s，解得NB

10、＝－1 N，負(fù)號表示管道對小球的作用力方向向上，選項C正確，D錯誤。 答案　AC 二、非選擇題 10．如圖9所示，內(nèi)壁光滑的彎曲鋼管固定在天花板上，一根結(jié)實的細(xì)繩穿過鋼管，兩端分別拴著一個小球A和B。小球A和B的質(zhì)量之比＝。當(dāng)小球A在水平面內(nèi)做勻速圓周運動時，小球A到管口的繩長為l，此時小球B恰好處于平衡狀態(tài)。管子的內(nèi)徑粗細(xì)不計，重力加速度為g。試求： 圖9 (1)拴著小球A的細(xì)繩與豎直方向的夾角θ； (2)小球A轉(zhuǎn)動的周期。 解析　(1)設(shè)細(xì)繩的拉力為F，小球B處于平衡狀態(tài)有 F＝mBg 在豎直方向上，小球A處于平衡狀態(tài)，有Fcos θ＝mAg 解得cos θ＝＝

11、所以拴著小球A的細(xì)繩與豎直方向的夾角θ＝60° (2)對于小球A，細(xì)繩拉力的水平分量提供圓周運動的向心力，有 Fsin θ＝mA r＝lsin θ 解得小球A的線速度為v＝ 又T＝ 則小球A轉(zhuǎn)動的周期T＝π。 答案　(1)60°　(2)π 11．(2016·湖南懷化三模)某高速公路的一個出口路段如圖10所示，情景簡化：轎車從出口A進(jìn)入匝道，先勻減速直線通過下坡路段至B點(通過B點前后速率不變)，再勻速率通過水平圓弧路段至C點，最后從C點沿平直路段勻減速到D點停下。已知轎車在A點的速度v0＝72 km/h，AB長L1＝150 m；BC為四分之一水平圓弧段，限速(允許通過的最大速度

12、)v＝36 km/h，輪胎與BC段路面間的動摩擦因數(shù)μ＝0.5，最大靜摩擦力可認(rèn)為等于滑動摩擦力，CD段為平直路段，長為L2＝50 m，重力加速度g取10 m/s2。 圖10 (1)若轎車到達(dá)B點速度剛好為v＝36 km/h，求轎車在AB下坡段加速度的大?。? (2)為保證行車安全，車輪不打滑，求水平圓弧段BC半徑R的最小值； (3)轎車從A點到D點全程的最短時間。 解析　(1)v0＝72 km/h＝20 m/s，AB長L1＝150 m，v＝36 km/h＝10 m/s，對AB段勻減速直線運動有v－v＝－2aL1，代入數(shù)據(jù)解得a＝1 m/s2。 (2)汽車在BC段做圓周運動，靜

13、摩擦力提供向心力，有f＝m，為了確保安全，則須滿足f≤μmg，解得R≥20 m，即Rmin＝20 m。 (3)設(shè)AB段時間為t1，BC段時間為t2，CD段時間為t3，全程所用最短時間為t。 L1＝t1·，而πR＝vt2， L2＝t3，t＝t1＋t2＋t3，解得t＝23.14 s。 答案　(1)1 m/s2　(2)20 m　(3)23.14 s 12．如圖11所示，固定的水平桌面上有一水平輕彈簧，右端固定在a點，彈簧處于自然狀態(tài)時其左端位于b點。桌面左側(cè)有一豎直放置且半徑R＝0.5 m的光滑半圓軌道MN，MN為豎直直徑。用質(zhì)量m＝0.2 kg的小物塊(視為質(zhì)點)將彈簧緩慢壓縮到c點，釋

14、放后從彈簧恢復(fù)原長過b點開始小物塊在水平桌面上的位移與時間的關(guān)系為x＝7t－2t2(m)。小物塊在N點進(jìn)入光滑半圓軌道，恰好能從M點飛出，飛出后落至水平桌面上的d點。取重力加速度g＝10 m/s2，彈簧始終在彈性限度內(nèi)，不計空氣阻力，求： 圖11 (1)d、N兩點間的距離； (2)b、N兩點間的距離； (3)物塊在N點時對半圓軌道的壓力。 解析　(1)由物塊恰好從M點飛出知，在M點物塊的重力恰好完全提供向心力，設(shè)其速度為vM，則mg＝m vM＝ m/s 物塊由M點水平飛出后，以初速度vM做平拋運動。 水平方向：xdN＝vMt 豎直方向：y＝2R＝gt2 代入數(shù)據(jù)解得xdN＝1 m (2)從N到M，由機(jī)械能守恒定律得 mv＋2mgR＝mv 解得vN＝5 m/s 物塊在bN段做勻減速運動，由x＝7t－2t2(m)知 初速度v0＝7 m/s，加速度a＝－4 m/s2 由v－v＝2axbN，得xbN＝3 m (3)物塊在N點時，設(shè)半圓軌道對物塊的支持力為N，由牛頓第二定律得N－mg＝m 解得N＝12 N 由牛頓第三定律得物塊在N點對半圓軌道的壓力大小為12 N，方向豎直向下。 答案　(1)1 m　(2)3 m　(3)12 N　方向豎直向下 9