《2022年高考數(shù)學(xué) 回扣突破練 第24練 算法初步與復(fù)數(shù) 文》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年高考數(shù)學(xué) 回扣突破練 第24練 算法初步與復(fù)數(shù) 文（11頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

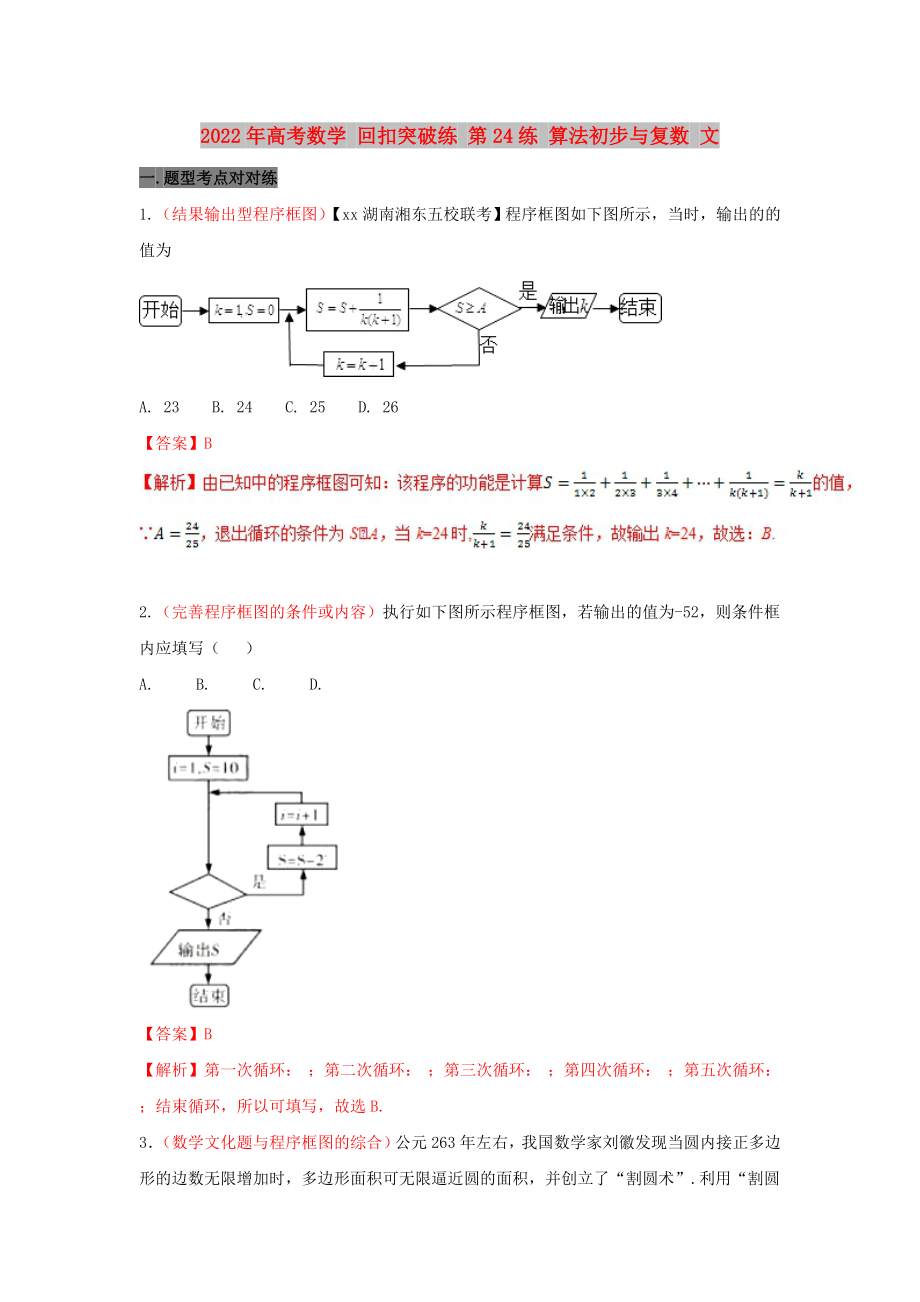
1、2022年高考數(shù)學(xué) 回扣突破練 第24練 算法初步與復(fù)數(shù) 文 一.題型考點(diǎn)對對練 1.（結(jié)果輸出型程序框圖）【xx湖南湘東五校聯(lián)考】程序框圖如下圖所示，當(dāng)時(shí)，輸出的的值為 A. 23 B. 24 C. 25 D. 26 【答案】B 2.（完善程序框圖的條件或內(nèi)容）執(zhí)行如下圖所示程序框圖，若輸出的值為-52，則條件框內(nèi)應(yīng)填寫（ ） A. B. C. D. 【答案】B 【解析】第一次循環(huán)： ；第二次循環(huán)： ；第三次循環(huán)： ；第四次循環(huán)： ；第五次循環(huán)： ；結(jié)束循環(huán)，所以可填寫，故選B. 3．（數(shù)學(xué)文化題與程序框圖

2、的綜合）公元263年左右，我國數(shù)學(xué)家劉徽發(fā)現(xiàn)當(dāng)圓內(nèi)接正多邊形的邊數(shù)無限增加時(shí)，多邊形面積可無限逼近圓的面積，并創(chuàng)立了“割圓術(shù)”.利用“割圓術(shù)”劉徽得到了圓周率精確到小數(shù)點(diǎn)后兩位的近似值 ，這就是著名的“微率”，如圖是利用劉徽的“割圓術(shù)”思想設(shè)計(jì)的一個(gè)程序框圖，則輸出的值為 （ ） （參考數(shù)據(jù)： ） A. B. C. D. 【答案】C 4．（算法與三角的交匯）【xx江西宜春六校聯(lián)考】執(zhí)行如圖所示的程序框圖，要使輸出的的值小于1，則輸入的值不能是下面的（ ） A. 4 B. 5 C. 6 D. 7 【答案】D ,

3、故C項(xiàng)符合題意.D項(xiàng)：當(dāng)?shù)扔?時(shí)， ，故D項(xiàng)不符合題意 5．（算法與函數(shù)的交匯）已知且，如圖所示的程序框圖的輸出值，則實(shí)數(shù)的取值范圍為（ ） A. B. C. D. 【答案】A 6．（算法與數(shù)列的交匯）執(zhí)行下邊的程序框圖，則輸出的的值為（ ） A. B. C. D. 【答案】B 【解析】，由程序框圖， ，當(dāng)時(shí)， ，故選B． 7．（利用復(fù)數(shù)的概念求解參數(shù)的規(guī)律）設(shè)i為虛數(shù)單位，若是純虛數(shù)，則a的值是 A. B. 0 C. 1 D. 2 【答案】C 8．（復(fù)數(shù)的幾

4、何意義的應(yīng)用規(guī)律）圖中網(wǎng)格紙的小正方形的邊長是1，復(fù)平面內(nèi)點(diǎn)所表示的復(fù)數(shù)滿足，則復(fù)數(shù)（ ） A. B. C. D. 【答案】B 【解析】由題得： ，所以 9．（復(fù)數(shù)代數(shù)運(yùn)算的技巧）設(shè)，其中是實(shí)數(shù)，則（ ） A. 1 B. C. D. 2 【答案】D 【解析】， .故選D. 10.（復(fù)數(shù)與數(shù)學(xué)文化題綜合）歐拉公式（為虛數(shù)單位）是由瑞士著名數(shù)學(xué)家歐拉發(fā)明的，它將指數(shù)函數(shù)的定義域擴(kuò)大到復(fù)數(shù)，建立了三角函數(shù)和指數(shù)函數(shù)的關(guān)系，它在復(fù)變函數(shù)論里非常重要，被譽(yù)為“數(shù)學(xué)中的天橋”，根據(jù)歐拉公式可知，表示的復(fù)數(shù)在復(fù)平面中位

5、于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 【答案】B 二.易錯(cuò)問題糾錯(cuò)練 11．（忽視先后順序不同對結(jié)果的影響）公元263年左右，我國數(shù)學(xué)家劉徽發(fā)現(xiàn)，當(dāng)圓內(nèi)接正多邊形的邊數(shù)無限增加時(shí)，正多邊形的周長可無限逼近圓的周長，并創(chuàng)立了割圓術(shù)，利用割圓術(shù)劉徽得到了圓周率精確到小數(shù)點(diǎn)后面兩位的近似值3．14，這就是著名的徽率，利用劉徽的割圓術(shù)設(shè)計(jì)的程序框圖如圖所示，若輸出的，則判斷框內(nèi)可以填入（ ）（參考數(shù)據(jù)： ， ， ） A. B. C. D. 【答案】B 【解析】通過比較和確定p的大小來確定框內(nèi)

6、所填內(nèi)容.時(shí)， ,否, , , 所以判斷框內(nèi) ,故判斷框內(nèi)可以填入 ,選B. 【注意問題】通過比較和確定p的大小來確定框內(nèi)所填內(nèi)容． 12．（對復(fù)數(shù)虛部概念理解不清至錯(cuò)）已知復(fù)數(shù)（其中為虛數(shù)單位），則的虛部為 A. B. C. D. 【答案】A 【注意問題】先對復(fù)數(shù)進(jìn)行化簡，復(fù)數(shù)的虛部不含i． 13．（循環(huán)結(jié)構(gòu)中忽視終止循環(huán)條件至錯(cuò)）程序框圖如圖所示，若輸入， ，則輸出的為__________． 【答案】57 【解析】由框圖可知，當(dāng)時(shí)結(jié)束循環(huán).第一次循環(huán)，得；第二次循環(huán)，得；第三次循環(huán)，得；第四次循環(huán)，得，不滿足循環(huán)條件，退出循環(huán)，輸

7、出． 【注意問題】由框圖可知，當(dāng)時(shí)結(jié)束循環(huán)． 14．（對復(fù)數(shù)為純虛數(shù)的條件不清至錯(cuò)）若復(fù)數(shù)為純虛數(shù)，則實(shí)數(shù)的值為__________． 【答案】3 【解析】純虛數(shù)要求是實(shí)部為零、虛部不為零.由題設(shè)，應(yīng)填答案. 【注意問題】純虛數(shù)要求是實(shí)部為零、虛部不為零． 三.新題好題好好練 15．若正整數(shù)除以正整數(shù)后的余數(shù)為，則記為，例如.下面程序框圖的算法源于我國古代聞名中外的《中國剩余定理》.執(zhí)行該程序框圖，則輸出的等于（ ） A. 32 B. 16 C. 8 D. 4 【答案】B 16．執(zhí)行如圖的程序框圖，已知輸出的.若輸入的，則實(shí)數(shù)的最大值為（

8、 ） A. 1 B. 2 C. 3 D. 4 【答案】D 【解析】由程序框圖有 ，當(dāng) 時(shí)， ，所以 ；當(dāng)時(shí)，由 有 ，綜上有 ，所以 的最大值為 . 故選D. 17．如圖所示的程序框圖中，如輸入，，則輸出（ ） A. 61 B. 62 C. 183 D. 184 【答案】C 18．執(zhí)行下圖程序框圖，如果輸入的， 均為2，則輸出的（ ） A. 7 B. 6 C. 5 D. 4 【答案】A 【解析】若，則第一次循環(huán)， 成立，則；第二次循環(huán)， 成立，則，此時(shí)不成立，輸出，故選A. 1

9、9．執(zhí)行如圖所示的程序框圖，若輸入的分別為1，2，0.3，則輸出的結(jié)果為（ ） A. 1.125 B. 1.25 C. 1.3125 D. 1.375 【答案】D 20.已知復(fù)數(shù)滿足，則復(fù)數(shù)在復(fù)平面內(nèi)對應(yīng)的點(diǎn)在（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】C 【解析】因?yàn)?，所以，?yīng)選答案C. 21.已知復(fù)數(shù)，若復(fù)數(shù)對應(yīng)的點(diǎn)在復(fù)平面內(nèi)位于第四象限，則實(shí)數(shù)的取值范圍是（ ） A. B. C. D. 【答案】A 22．已知復(fù)數(shù)，其中是虛數(shù)單位，則的虛部為（ ） A. 1 B. -1 C. D. 【答案】A 【解析】，由的冪的周期性可知，虛部為1,故選A． 23．若復(fù)數(shù)，在復(fù)平面內(nèi)對應(yīng)的點(diǎn)關(guān)于軸對稱，且，則復(fù)數(shù)在復(fù)平面內(nèi)對應(yīng)的點(diǎn)在（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】B 【解析】,所以在復(fù)平面內(nèi)對應(yīng)的點(diǎn)為,在第二象限 24．設(shè)復(fù)數(shù)滿足（其中為虛數(shù)單位），則（ ） A. B. C. D. 【答案】C 【解析】因?yàn)椋詰?yīng)選答案C.