《河南省2022年中考數(shù)學(xué)總復(fù)習(xí) 第七章 圖形的變化提分特訓(xùn)》由會(huì)員分享，可在線閱讀，更多相關(guān)《河南省2022年中考數(shù)學(xué)總復(fù)習(xí) 第七章 圖形的變化提分特訓(xùn)（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

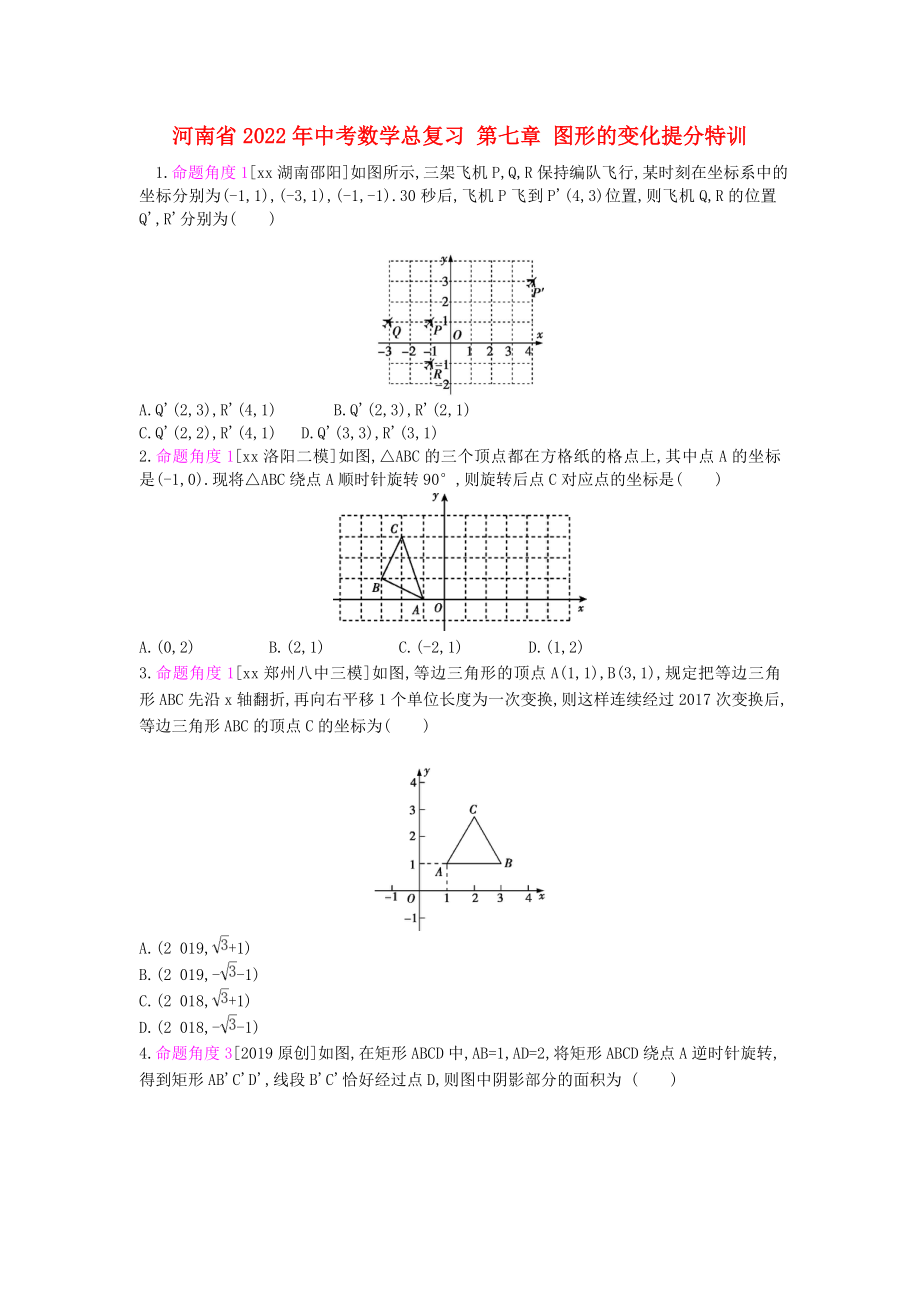
1、河南省2022年中考數(shù)學(xué)總復(fù)習(xí) 第七章 圖形的變化提分特訓(xùn) 1.命題角度1[xx湖南邵陽]如圖所示,三架飛機(jī)P,Q,R保持編隊(duì)飛行,某時(shí)刻在坐標(biāo)系中的坐標(biāo)分別為(-1,1),(-3,1),(-1,-1).30秒后,飛機(jī)P飛到P'(4,3)位置,則飛機(jī)Q,R的位置Q',R'分別為(　　) 　　　　　　　　　　　　　　　　　　 A.Q'(2,3),R'(4,1)　　 B.Q'(2,3),R'(2,1) C.Q'(2,2),R'(4,1) D.Q'(3,3),R'(3,1) 2.命題角度1[xx洛陽二模]如圖,△ABC的三個(gè)頂點(diǎn)都在方格紙的格點(diǎn)上,其中點(diǎn)A的坐標(biāo)是(-1,0).現(xiàn)將

2、△ABC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°,則旋轉(zhuǎn)后點(diǎn)C對應(yīng)點(diǎn)的坐標(biāo)是(　　) A.(0,2)　　　 B.(2,1)　　　 C.(-2,1)　　　 D.(1,2) 3.命題角度1[xx鄭州八中三模]如圖,等邊三角形的頂點(diǎn)A(1,1),B(3,1),規(guī)定把等邊三角形ABC先沿x軸翻折,再向右平移1個(gè)單位長度為一次變換,則這樣連續(xù)經(jīng)過2 017次變換后,等邊三角形ABC的頂點(diǎn)C的坐標(biāo)為(　　) 　　　　　　　　　　　　　　　　　　 A.(2 019,+1) B.(2 019,--1) C.(2 018,+1) D.(2 018,--1) 4.命題角度3[2019原創(chuàng)]如圖,在矩形A

3、BCD中,AB=1,AD=2,將矩形ABCD繞點(diǎn)A逆時(shí)針旋轉(zhuǎn),得到矩形AB'C'D',線段B'C'恰好經(jīng)過點(diǎn)D,則圖中陰影部分的面積為 (　　) A. B. C.π D.π-1 5.命題角度2[xx山東濰坊]如圖,將一張矩形紙片ABCD的邊BC斜著向AD邊對折,使點(diǎn)B落在AD上,記為B',折痕為CE;再將CD邊斜向下對折,使點(diǎn)D落在B'C上,記為D',折痕為CG,B'D'=2,BE=BC.則矩形紙片ABCD的面積為　　　　.? 參考答案 第二節(jié)　圖形的對稱、平移與旋轉(zhuǎn) 1.A　將點(diǎn)P的橫坐標(biāo)加5、縱坐標(biāo)加2得到點(diǎn)P'(4,3),故點(diǎn)Q,R的對應(yīng)點(diǎn)Q',R'的坐標(biāo)分別為(

4、-3+5,1+2),(-1+5,-1+2),即Q'(2,3),R'(4,1). 2.B　由題意畫出旋轉(zhuǎn)后的△AB'C'(點(diǎn)B',C'分別是點(diǎn)B,C的對應(yīng)點(diǎn)),如圖所示,則C'(2,1),即旋轉(zhuǎn)后點(diǎn)C對應(yīng)點(diǎn)的坐標(biāo)是(2,1). 3.B　由點(diǎn)A,B的坐標(biāo)可知,等邊三角形ABC的邊長為2,則在初始位置時(shí),點(diǎn)C到x軸,y軸的距離分別為+1,2.由題意可知,經(jīng)過偶數(shù)次變換,△ABC位于第一象限,經(jīng)過奇數(shù)次變換,△ABC位于第四象限.故經(jīng)過2 017次變換,△ABC位于第四象限,點(diǎn)C的縱坐標(biāo)是--1;第1次變換后,點(diǎn)C的橫坐標(biāo)為3,第3次變換后,點(diǎn)C的橫坐標(biāo)為5,第5次變換后,點(diǎn)C的橫坐標(biāo)為7……

5、∴第2 017次變換后,點(diǎn)C的橫坐標(biāo)為2+2 017=2 019,故第2 017次變換后,點(diǎn)C的坐標(biāo)為(2 019,--1). 4.B　如圖,連接AC',AC,在Rt△ABC中,AB=1,BC=2,∴AC==.在Rt△AB'D中,∵AB'=AB=1,AD=2,∴∠ADB'=30°,∴∠B'AD=60°,∴∠CAC'=∠BAB'=30°,∴S陰影部分=S扇形ACC'+S△ABC-S扇形ABB'-S△AB'C'=S扇形ACC'-S扇形ABB'=-=.故選B. 5.15　設(shè)CD=CD'=AB=x,則BC=B'C=x+2,BE=B'E=BC=(x+2),∴AE=AB-BE=x-(x+2)=(x-1).易證Rt△AB'E∽R(shí)t△DCB',∴=,即=,解得DB'=2(x-1).在Rt△B'CD中,由B'C2=CD2+B'D2,得(x+2)2=x2+4(x-1)2,解得x1=3,x2=0(舍去),∴CD=3,BC=x+2=5,則矩形ABCD的面積為15.