《2020年全國高考數(shù)學第二輪復習 專題升級訓練13 用空間向量的方法解立體幾何問題 理》由會員分享，可在線閱讀，更多相關《2020年全國高考數(shù)學第二輪復習 專題升級訓練13 用空間向量的方法解立體幾何問題 理（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、專題升級訓練13　用空間向量的方法解立體幾何問題 (時間：60分鐘　滿分：100分) 一、選擇題(本大題共6小題，每小題6分，共36分) 1．平面α的一個法向量n＝(1，－1,0)，則y軸與平面α所成的角的大小為(　　)． A． 　　　　 B．　　　　　C． 　　　　 D． 2．在二面角α－l－β中，平面α的法向量為n，平面β的法向量為m，若〈n，m〉＝130°，則二面角α－l－β的大小為(　　)． A．50°　　　　B．130°　　　　C．50°或130°　　　D．可能與130°毫無關系 3．直三棱柱ABC－A1B1C1中，∠ACB＝90°，∠BAC＝30°，BC＝1，AA1＝

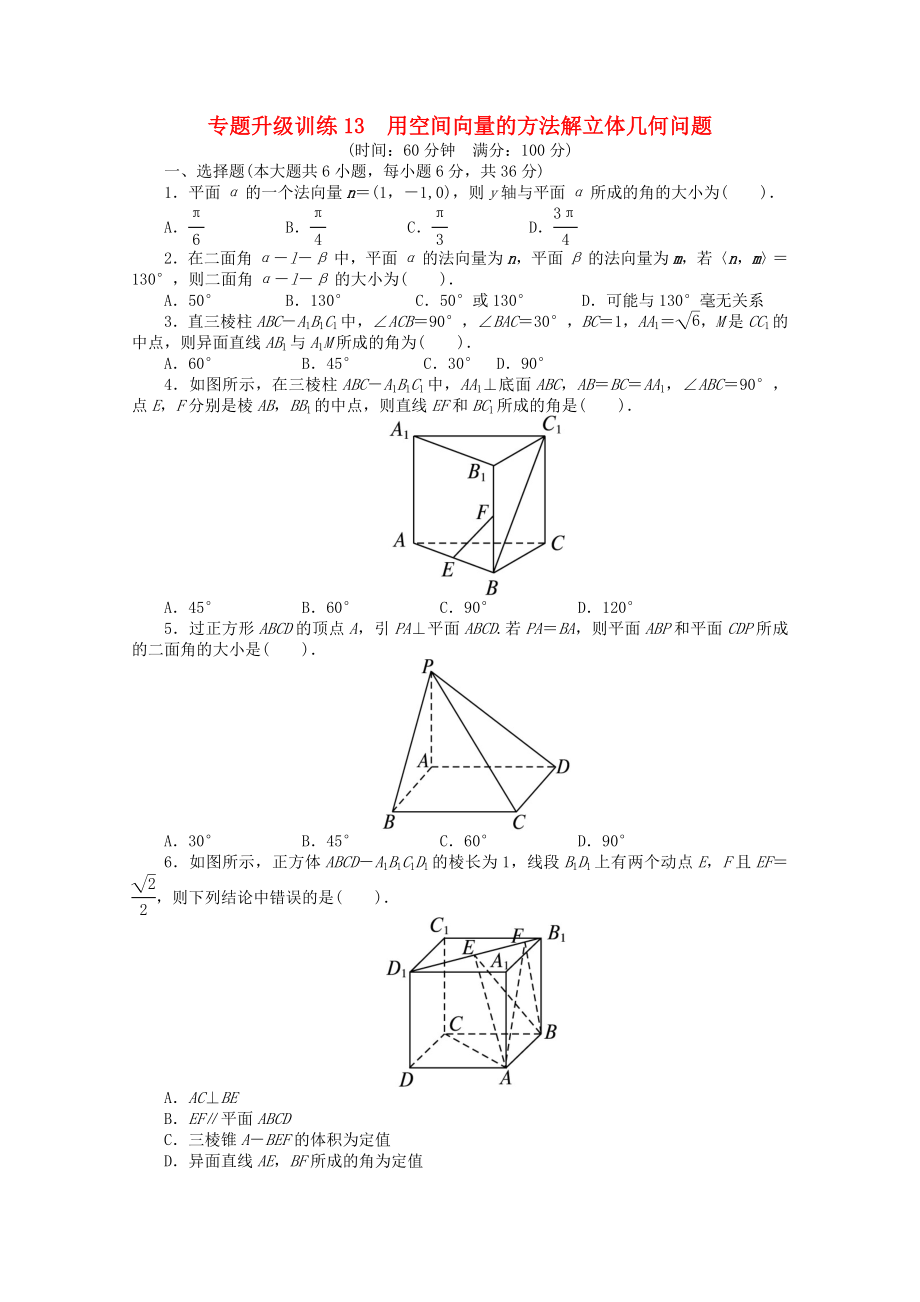
2、，M是CC1的中點，則異面直線AB1與A1M所成的角為(　　)． A．60° 　　　　 B．45°　　　　C．30° D．90° 4．如圖所示，在三棱柱ABC－A1B1C1中，AA1⊥底面ABC，AB＝BC＝AA1，∠ABC＝90°，點E，F(xiàn)分別是棱AB，BB1的中點，則直線EF和BC1所成的角是(　　)． A．45° 　　　　 B．60° 　　　　 C．90°　　　　 D．120° 5．過正方形ABCD的頂點A，引PA⊥平面ABCD.若PA＝BA，則平面ABP和平面CDP所成的二面角的大小是(　　)． A．30° 　　　　 B．45° 　　　　 C．60° 　　　　 D

3、．90° 6．如圖所示，正方體ABCD－A1B1C1D1的棱長為1，線段B1D1上有兩個動點E，F(xiàn)且EF＝，則下列結論中錯誤的是(　　)． A．AC⊥BE B．EF∥平面ABCD C．三棱錐A－BEF的體積為定值 D．異面直線AE，BF所成的角為定值 二、填空題(本大題共3小題，每小題6分，共18分) 7．如圖所示，在棱長為1的正方體ABCD－A1B1C1D1中，M和N分別是A1B1和BB1的中點，那么直線AM與CN所成角的余弦值為__________． 8．正四棱錐S－ABCD中，O為頂點在底面上的射影，P為側棱SD的中點，且SO＝OD，則直線BC與平面PAC所成的角

4、是__________． 9．在空間直角坐標系中有棱長為a的正方體ABCD－A1B1C1D1，點M是線段DC1上的動點，則點M到直線AD1距離的最小值是__________． 三、解答題(本大題共3小題，共46分．解答應寫出必要的文字說明、證明過程或演算步驟) 10．(本小題滿分15分)如圖，四邊形ABCD為正方形，PD⊥平面ABCD，PD＝AD＝2. (1)求PC與平面PBD所成的角； (2)在線段PB上是否存在一點E，使得PC⊥平面ADE？并說明理由． 11．(本小題滿分15分)(2020·湖南高考，理19)如圖，在圓錐PO中，已知PO＝，⊙O的直徑AB＝2，C是的中點

5、，D為AC的中點． (1)證明：平面POD⊥平面PAC； (2)求二面角B－PA－C的余弦值． 12．(本小題滿分16分)(2020·廣東高考，理18)如圖，在錐體P－ABCD中，ABCD是邊長為1的菱形，且∠DAB＝60°，PA＝PD＝，PB＝2，E，F(xiàn)分別是BC，PC的中點． (1)證明：AD⊥平面DEF； (2)求二面角P－AD－B的余弦值． 參考答案 一、選擇題 1．B 2．C　解析：因為二面角的范圍是[0°，180°]，由法向量的夾角與二面角的大小相等或互補，可知二面角的大小可能是130°也可能是50°. 3．D　解析：建立坐標系如圖所示， 易得

6、M，A1(0，，0)，A(0，，)，B1(1,0,0)， ∴＝(1，－，－)， ＝. ∴＝1×0＋3－＝0， ∴，即AB1⊥A1M. 4．B　5．B　6．D 二、填空題 7．　解析：以D為坐標原點，為x軸，為y軸，為z軸，建立空間直角坐標系，如圖所示． 則A(1,0,0)，M，C(0,1,0)，N， ∴＝，＝. 設直線AM與CN所成的角為θ， 則cos θ＝|cos〈〉|＝ ＝＝. 8．30°　解析：如圖所示，以O為原點建立空間直角坐標系O－xyz. 設OD＝SO＝OA＝OB＝OC＝a， 則A(a,0,0)，B(0，a,0)，C(－a,0,0)，P， 則

7、＝(2a,0,0)， ＝，． 設平面PAC的法向量為n，可求得n＝(0,1,1)， 則cos〈，n〉＝＝＝. ∴〈，n〉＝60°， ∴直線BC與平面PAC所成的角為90°－60°＝30°. 9．a(chǎn)　解析：以D為原點建立空間直角坐標系(如原圖所示)， 則A(a,0,0)，D1(0,0，a)． 設M(0，x，x)(0≤x≤a)， 有＝(－a，x，x)，＝(－a,0，a)， 則cos〈〉＝＝， 則點M到直線AD1的距離d為 ＝· ， ∴當x＝時，dmin＝a. 三、解答題 10．解：(1)連接AC，設AC∩BD＝O，連接PO. 因為PD⊥平面ABCD，CO?平面

8、ABCD，所以PD⊥CO. 由ABCD為正方形，知CO⊥BD. 又PD∩BD＝D，所以CO⊥平面PBD. 所以∠CPO是PC與平面PBD所成的角． 在Rt△POC中，sin∠CPO＝＝＝， 所以∠CPO＝，即PC與平面PBD所成的角為. (2)建立如圖所示的空間直角坐標系D－xyz. 設線段PB上存在點E，使得PC⊥平面ADE. 則存在實數(shù)λ，使得＝(0≤λ≤1)． 因為P(0,0,2)，B(2,2,0)，所以＝(2,2，－2)， ＋＝(0,0,2)＋λ(2,2，－2) ＝(2λ，2λ，2－2λ)． 由題意，顯然有AD⊥平面PCD，所以PC⊥AD. 要使PC⊥平面

9、ADE，只需再有， 即，即0·(2λ)＋2·(2λ)－2(2－2λ)＝0. 解得λ＝∈[0,1]． 故在線段PB上存在一點E(E為線段PB的中點)，使得PC⊥平面ADE. 11．解法一：(1)連接OC，因為OA＝OC， D是AC的中點，所以AC⊥OD. 又PO⊥底面⊙O，AC?底面⊙O，所以AC⊥PO.因為OD，PO是平面POD內(nèi)的兩條相交直線，所以AC⊥平面POD.而AC?平面PAC，所以平面POD⊥平面PAC. (2)在平面POD中，過O作OH⊥PD于H，由(1)知，平面POD⊥平面PAC，所以OH⊥平面PAC. 又PA?平面PAC，所以PA⊥OH. 在平面PAO中，

10、過O作OG⊥PA于G，連接HG，則有PA⊥平面OGH，從而PA⊥HG，故∠OGH為二面角B－PA－C的平面角． 在Rt△ODA中，OD＝OA·sin 45°＝. 在Rt△POD中，. 在Rt△POA中，. 在Rt△OHG中，. 所以cos ∠OGH＝. 故二面角B－PA－C的余弦值為. 解法二：(1)如圖所示，以O為坐標原點，OB，OC，OP所在直線分別為x軸，y軸，z軸建立空間直角坐標系．則 O(0,0,0)，A(－1,0,0)，B(1,0,0)，C(0,1,0)，P(0,0，)，D(，,0)． 設n1＝(x1，y1，z1)是平面POD的一個法向量，則由n1·，n1·，得

11、 所以z1＝0，x1＝y(tǒng)1.取y1＝1，得n1＝(1,1,0)． 設n2＝(x2，y2，z2)是平面PAC的一個法向量，則由，，得 所以x2＝－z2，y2＝z2，取z2＝1，得n2＝(－，，1)． 因為n1·n2＝(1,1,0)·(－，，1)＝0，所以n1⊥n2.從而平面POD⊥平面PAC. (2)因為y軸⊥平面PAB，所以平面PAB的一個法向量為n3＝(0,1,0)．由 (1)知，平面PAC的一個法向量為n2＝(－，，1)． 設向量n2和n3的夾角為θ，則cos θ＝＝＝. 由圖可知，二面角B－PA－C的平面角與θ相等，所以二面角B－PA－C的余弦值為. 12．解法一：(1

12、)證明：取AD中點G，連接PG，BG，BD. 因PA＝PD，有PG⊥AD，在△ABD中，AB＝AD＝1，∠DAB＝60°，有△ABD為等邊三角形，因此BG⊥AD，BG∩PG＝G， 所以AD⊥平面PBG?AD⊥PB，AD⊥GB. 又PB∥EF，得AD⊥EF，而DE∥GB得AD⊥DE， 又FE∩DE＝E，所以AD⊥平面DEF. (2)∵PG⊥AD，BG⊥AD， ∴∠PGB為二面角P－AD－B的平面角． 在Rt△PAG中，PG2＝PA2－AG2＝， 在Rt△ABG中，BG＝AB·sin 60°＝， ∴cos∠PGB＝＝＝－. 解法二：(1)證明：取AD中點為G，因為PA＝PD

13、，所以PG⊥AD. 又AB＝AD，∠DAB＝60°，△ABD為等邊三角形， 因此，BG⊥AD，從而AD⊥平面PBG. 延長BG到O且使得PO⊥OB， 又PO?平面PBG，PO⊥AD，AD∩OB＝G， 所以PO⊥平面ABCD. 以O為坐標原點，菱形的邊長為單位長度，直線OB，OP分別為x軸，z軸，平行于AD的直線為y軸，建立如圖所示空間直角坐標系． 設P(0,0，m)，G(n,0,0)，則A，D. ∵sin 60°＝， ∴B，C，E， F. 由于＝(0,1,0)，＝，＝， 得＝0，＝0，AD⊥DE，AD⊥FE，DE∩FE＝E， ∴AD⊥平面DEF. (2)∵＝，＝， ∴，， 解之，得m＝1，n＝. 取平面ABD的法向量n1＝(0,0，－1)， 設平面PAD的法向量n2＝(a，b，c)， 由，得a－－c＝0， 由，得a＋－c＝0， 取n2＝.∴cos〈n1，n2〉＝＝－.