《高中數(shù)學(xué) 第二章 第9課時(shí)《平面上兩點(diǎn)間的距離》教案（學(xué)生版 ） 蘇教版必修2》由會(huì)員分享，可在線閱讀，更多相關(guān)《高中數(shù)學(xué) 第二章 第9課時(shí)《平面上兩點(diǎn)間的距離》教案（學(xué)生版 ） 蘇教版必修2（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

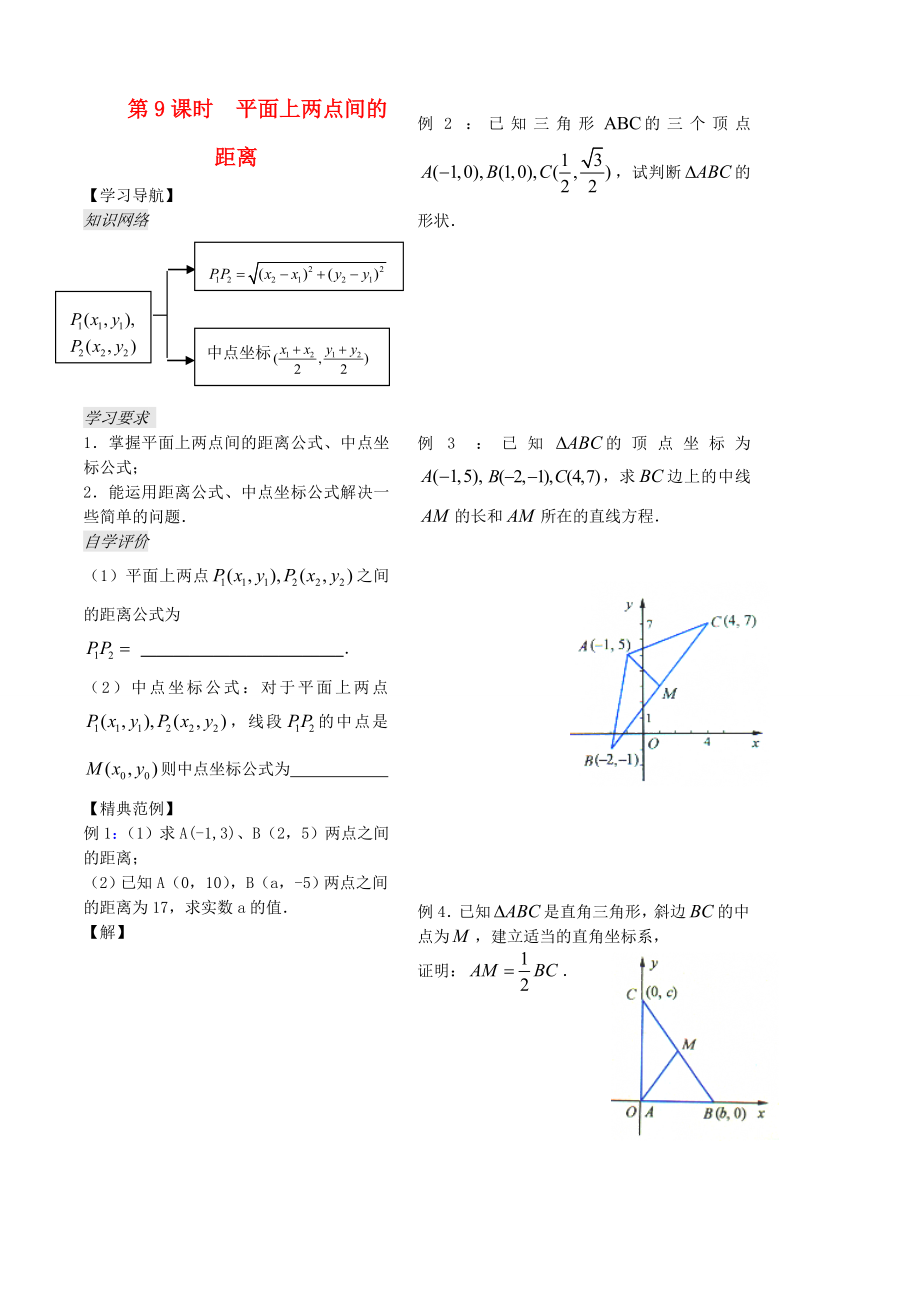
1、第9課時(shí) 平面上兩點(diǎn)間的距離 【學(xué)習(xí)導(dǎo)航】 知識(shí)網(wǎng)絡(luò) 中點(diǎn)坐標(biāo) 學(xué)習(xí)要求 1．掌握平面上兩點(diǎn)間的距離公式、中點(diǎn)坐標(biāo)公式； 2．能運(yùn)用距離公式、中點(diǎn)坐標(biāo)公式解決一些簡(jiǎn)單的問題． 自學(xué)評(píng)價(jià) （1）平面上兩點(diǎn)之間的距離公式為 _________________________． （2）中點(diǎn)坐標(biāo)公式：對(duì)于平面上兩點(diǎn)，線段的中點(diǎn)是則中點(diǎn)坐標(biāo)公式為　　　　　　　　　　　　　　 【精典范例】 例1：（1）求A(-1,3)、B（2，5）兩點(diǎn)之間的距離； （2）已知A（0，10），B（a，-5）兩點(diǎn)之間的距離為17，求實(shí)數(shù)a的

2、值． 【解】 例2：已知三角形的三個(gè)頂點(diǎn)，試判斷的形狀． 例3：已知的頂點(diǎn)坐標(biāo)為，求邊上的中線的長(zhǎng)和所在的直線方程． 例4．已知是直角三角形，斜邊的中點(diǎn)為，建立適當(dāng)?shù)闹苯亲鴺?biāo)系， 證明：． 追蹤訓(xùn)練一 1.式子可以理解為(　　) 兩點(diǎn)(a,b)與(1,-2)間的距離 兩點(diǎn)(a,b)與(-1,2)間的距離 兩點(diǎn)(a,b)與(1,2)間的距離 兩點(diǎn)(a,b)與(-1,-2)間的距離 2.以A(3,-1)

3、, B(1,3)為端點(diǎn)的線段的垂直平分線的方程為 　(　　) 2x+y-5=0 2x+y+6=0 x-2y=0 x-2y-8=0 3. 線段AB的中點(diǎn)坐標(biāo)是(-2,3),又點(diǎn)A的坐標(biāo)是(2,-1),則點(diǎn)B的坐標(biāo)是　　　　　　?。? 4．已知點(diǎn)，若點(diǎn)在直線上，求取最小值． 【選修延伸】 對(duì)稱性問題 例5: 已知直線，（1）求點(diǎn)關(guān)于對(duì)稱的點(diǎn)；（2）求關(guān)于點(diǎn)對(duì)稱的直線方程． 聽課隨筆 例6：一條光線經(jīng)過點(diǎn),射在直線上，反射后，經(jīng)過點(diǎn)，求光線的入射線和反射線所在的直

4、線方程． 思維點(diǎn)拔： 平面上兩點(diǎn)間的距離公式為，線段中點(diǎn)坐標(biāo)為.平面上兩點(diǎn)間距離公式及中點(diǎn)坐標(biāo)公式有著廣泛的應(yīng)用，如：計(jì)算圖形面積，判斷圖形形狀等.同時(shí)也要注意掌握利用中點(diǎn)坐標(biāo)公式處理對(duì)稱性問題. 追蹤訓(xùn)練二 1．點(diǎn)(-1,2)關(guān)于直線x+y-3=0的對(duì)稱點(diǎn)的坐 標(biāo)為 (　　) (1,4) (-1,4) (1,-4) (-1,-4) 2．直線3x-y-2=0關(guān)于x軸對(duì)稱的直線方程為　　　　　　　　　?。? 3．已知點(diǎn),試求點(diǎn)的坐標(biāo),使四邊形為等腰梯形． 4