《2020版高考數(shù)學(xué)一輪復(fù)習(xí) 單元質(zhì)檢卷八 立體幾何（A）理 北師大版》由會員分享，可在線閱讀，更多相關(guān)《2020版高考數(shù)學(xué)一輪復(fù)習(xí) 單元質(zhì)檢卷八 立體幾何（A）理 北師大版（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

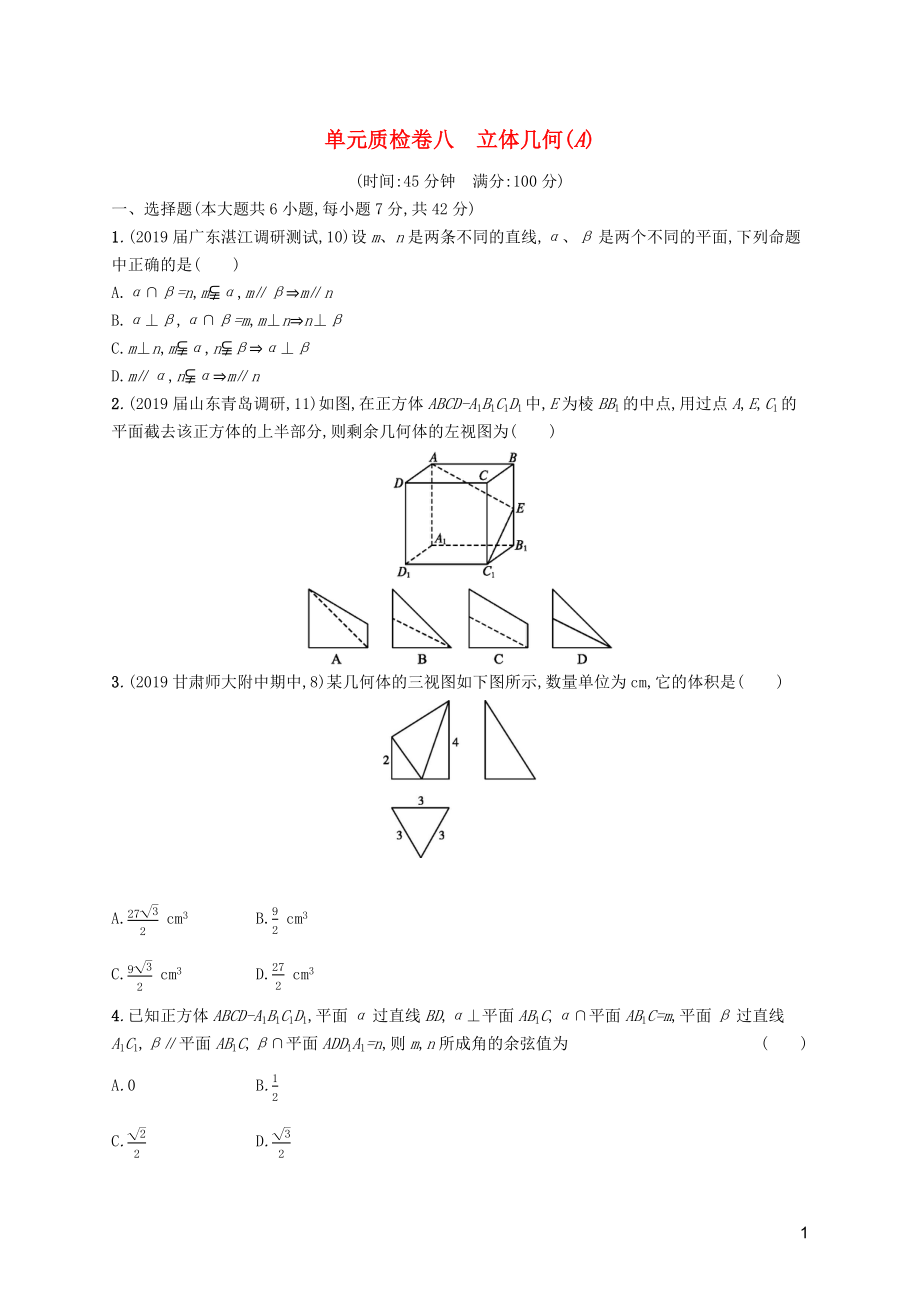
1、單元質(zhì)檢卷八　立體幾何(A) (時間:45分鐘　滿分:100分) 一、選擇題(本大題共6小題,每小題7分,共42分) 1.(2019屆廣東湛江調(diào)研測試,10)設(shè)m、n是兩條不同的直線,α、β是兩個不同的平面,下列命題中正確的是(　　) A.α∩β=n,m?α,m∥β?m∥n B.α⊥β,α∩β=m,m⊥n?n⊥β C.m⊥n,m?α,n?β?α⊥β D.m∥α,n?α?m∥n 2.(2019屆山東青島調(diào)研,11)如圖,在正方體ABCD-A1B1C1D1中,E為棱BB1的中點,用過點A,E,C1的平面截去該正方體的上半部分,則剩余幾何體的左視圖為(　　) 3.(2019

2、甘肅師大附中期中,8)某幾何體的三視圖如下圖所示,數(shù)量單位為cm,它的體積是(　　) 　　　　　　　　　　　　　　　 A.2732 cm3 B.92 cm3 C.932 cm3 D.272 cm3 4.已知正方體ABCD-A1B1C1D1,平面α過直線BD,α⊥平面AB1C,α∩平面AB1C=m,平面β過直線A1C1,β∥平面AB1C,β∩平面ADD1A1=n,則m,n所成角的余弦值為(　　) A.0 B.12 C.22 D.32 5.(2019屆湖南桃江一中期中,5)某幾何體的三視圖如圖所示,則該幾何體的外接球的表面積為(　　) A.25π B.26π C.32π

3、D.36π 6.已知某三棱錐的三視圖如圖所示,圖中的3個直角三角形的直角邊長度已經(jīng)標(biāo)出,則在該三棱錐中,最短的棱和最長的棱所在直線所成角的余弦值為(　　) A.13 B.55 C.12 D.23 二、填空題(本大題共2小題,每小題7分,共14分) 7.(2019廣東深圳實驗中學(xué)、珠海一中等六校聯(lián)考,15)在三棱錐D-ABC中,DC⊥底面ABC,AD=6,AB⊥BC且三棱錐D-ABC的每個頂點都在球O的表面上,則球O的表面積為　　　　　.? 8.如圖,在三棱錐S-ABC中,SA=SB=SC,且∠ASB=∠BSC=∠CSA=π2,M、N分別是AB和SC的中點.則異面直線SM與BN

4、所成的角的余弦值為　　　　　,直線SM與平面SAC所成角的大小為　　　　　.? 三、解答題(本大題共3小題,共44分) 9.(14分)如圖,在三棱錐S-ABC中,平面SAB⊥平面ABC,△SAB是等邊三角形,已知AC=2AB=4,BC=25. (1)求證:平面SAB⊥平面SAC; (2)求二面角B-SC-A的余弦值. 10.(15分)(2019湖南師范大學(xué)附中模擬,18)如圖,α∩β=l,二面角α-l-β的大小為θ,A∈α,B∈β,點A在直線l上的射影為A1,點B在直線l上的射影為B1.已知AB=2,AA1=1,BB1=2. (1)若

5、θ=120°,求直線AB與平面β所成角的正弦值; (2)若θ=90°,求二面角A1-AB-B1的余弦值. 11.(15分)(2019屆江蘇徐州期中)如圖,在平行四邊形ABCD中,AB=1,AD=2,∠ABC=π3,四邊形ACEF為矩形,平面ACEF⊥平面ABCD,AF=1,點M在線段EF上運動,且EM=λEF. (1)當(dāng)λ=12時,求異面直線DE與BM所成角的大小; (2)設(shè)平面MBC與平面ECD所成二面角的大小為θ0<θ≤π2,求cos θ的取值范圍. 參考答案 單元質(zhì)檢卷八　立體幾何(A)

6、 1.A　對于A,根據(jù)線面平行性質(zhì)定理即可得A選項正確;對于B,當(dāng)α⊥β,α∩β=m時,若n⊥m,n?α,則n⊥β,但題目中無條件n?α,故B不一定成立;對于C,若m⊥n,m?α,n?β,則α與β相交或平行,故C錯誤;對于D,若m∥α,n?α,則m與n平行或異面,則D錯誤,故選A. 2.C　取DD1中點F,連接AF,C1F,平面AFC1E為截面.如下圖,所以下半部分的左視圖如C選項,所以選C. 3.C　根據(jù)三視圖可將其還原為如下直觀圖, V=13S·h=13×12×(2+4)×3×332=932,故選C. 4.D　如圖所示,∵BD1⊥平面AB1C,平面α過直線BD,α⊥平面AB

7、1C, ∴平面α即為平面DBB1D1. 設(shè)AC∩BD=O, ∴α∩平面AB1C=OB1=m. ∵平面A1C1D過直線A1C1,與平面AB1C平行,而平面β過直線A1C1,β∥平面AB1C, ∴平面A1C1D即為平面β.β∩平面ADD1A1=A1D=n, 又A1D∥B1C, ∴m,n所成角為∠OB1C, 由△AB1C為正三角形,則cos∠OB1C=cosπ6=32.故選D. 5.C　三視圖對應(yīng)的幾何體如圖所示,其中DA⊥平面ABC,∠ABC=90°,所以該四面體的四個面都是直角三角形且DA=4,AC=4,故四面體外接球的直徑為DC=42,故外接球的表面積為4π×(22)2=

8、32π,故選C. 6.A　由三視圖還原幾何體如圖. 幾何體是三棱錐A-BCD,滿足平面ACD⊥平面BCD,且AD⊥CD,BC⊥CD. 最短棱為CD,最長棱為AB.在平面BCD內(nèi),過點B作BE∥CD,且BE=CD,連接DE, ∴四邊形BEDC為正方形,可得AE=22,在Rt△AEB中,求得AB=12+(22)2=3, ∴cos∠ABE=BEAB=13. 即最短的棱和最長的棱所在直線所成角的余弦值為13.故選A. 7.36π　因為三棱錐D-ABC中,DC⊥底面ABC,所以DC⊥AB,又因為AB⊥BC,DC和CB相交于點C,故得到AB⊥面BCD,故得到AB垂直于BD,又因為DC

9、垂直于面ABC,故DC垂直于AC,故三角形ACD和三角形ABD均為直角三角形,有公共斜邊AD,取AD中點為O點,根據(jù)直角三角形斜邊的中點為外心得到O到A、B、C、D四個點的距離相等,故點O是球心,球的半徑為3,由球的面積公式得S=4πR2=36π.故答案為36π. 8.105　π4　因為∠ASB=∠BSC=∠CSA=π2,所以以S為坐標(biāo)原點,SA,SB,SC為x,y,z軸建立空間直角坐標(biāo)系. 設(shè)SA=SB=SC=2,則M(1,1,0),B(0,2,0),N(0,0,1),A(2,0,0),C(0,0,2). 因為SM=(1,1,0),BN=(0,-2,1),cos=-22×

10、5=-105, 所以異面直線SM與BN所成的角的余弦值為105,平面SAC一個法向量為SB=(0,2,0),則由cos=22×2=22得=π4,即直線SM與平面SAC所成角大小為π4. 9.(1)證明在△BCA中,∵AB=2,CA=4,BC=25, ∴AB2+AC2=BC2,故AB⊥AC. 又平面SAB⊥平面ABC,平面SAB∩平面ABC=AB,∴AC⊥平面SAB. 又AC?平面SAC,所以平面SAB⊥平面SAC. (2)解如圖建立空間直角坐標(biāo)系,A(0,0,0),B(2,0,0),S(1,0,3),C(0,4,0), CS=(1,-4,3),BC

11、=(-2,4,0),AC=(0,4,0), 設(shè)平面SBC的法向量n=(x,y,z),由-2x+4y=0,x-4y+3z=0,則n=2,1,233. 設(shè)平面SCA的法向量m=(a,b,c),由4b=0,a-4b+3c=0, ∴m=(-3,0,1),∴cos=-21919, ∴二面角B-SC-A的余弦值為21919. 10.解 (1)如圖,過點A作平面β的垂線交于點G,連接GB、GA1, 因為AG⊥β,所以∠ABG是AB與β所成的角.在Rt△GA1A中,∠GA1A=60°,AA1=1,∴AG=32. 在Rt△AGB中,AB=2,AG=32,sin∠ABG=34,故AB與

12、平面β所成的角的正弦值為34. (2)如圖,建立坐標(biāo)系, 則A1(0,0,0),A(0,0,1),B1(0,1,0),B(2,1,0). 在AB上取一點F(x,y,z),則存在t∈R,使得AF=tAB,即(x,y,z-1)=t(2,1,-1), ∴點F的坐標(biāo)為(2t,t,1-t). 要使A1F⊥AB,須A1F·AB=0, 即(2t,t,1-t)·(2,1,-1)=0,2t+t-(1-t)=0,解得t=14, ∴點F的坐標(biāo)為24,14,34, ∴A1F=24,14,34. 設(shè)E為AB1的中點,則點E的坐標(biāo)為0,12,12. ∴EF=24,-14,14. 又EF·AB=2

13、4,-14,14·(2,1,-1)=12-14-14=0, ∴EF⊥AB, ∴∠A1FE為所求二面角的平面角.又cos∠A1FE=A1F·EF|A1F||EF|=(24,14,34)·(24,-14,14)216+116+916·216+116+116=18-116+31634×14=13=33, ∴二面角A1-AB-B1的余弦值為32. 11.解 (1)在△ABC中,AB=1,BC=AD=2,∠ABC=π3,則AC=3,所以AB2+AC2=BC2,即∠BAC=90°.因為四邊形ACEF為矩形,所以FA⊥AC,因為平面ACEF⊥平面ABCD,平面ACEF∩平面ABCD=AC,FA?平面

14、ACEF,所以FA⊥平面ABCD. 建立如圖所示的空間直角坐標(biāo)系, 則A(0,0,0),B(1,0,0),C(0,3,0),D(-1,3,0),E(0,3,1),F(0,0,1), 當(dāng)λ=12時,EM=12EF, 所以M0,32,1. 所以BM=-1,32,1,DE=(1,0,1), 所以BM·DE=(1,0,1)·-1,32,1=0,所以BM⊥DE,即異面直線DE與BM所成角的大小為90°. (2)平面ECD的一個法向量n1=(0,1,0),設(shè)M(x0,y0,z0),由EM=λ(0,-3,0)=(0,-3λ,0)=(x0,y0-3,z0-1),得x0=0,y0=3(1-λ),z0=1,即M(0,3(1-λ),1),所以BM=(-1,3(1-λ),1),BC=(-1,3,0). 設(shè)平面MBC的法向量n2=(x,y,z),因為n2⊥BC,n2⊥BM, 即-x+3y=0,-x+3(1-λ)y+z=0, 取y=1,則x=3,z=3λ, 所以平面MBC的一個法向量n2=(3,1,3λ), 因為0<θ≤π2, 所以cos θ=n1·n2|n1||n2|=14+3λ2. 因為0≤λ≤1,所以cos θ∈77,12. 9