《北師大版八年級(jí)下冊(cè)數(shù)學(xué) 1.4角平分線 同步練習(xí)題》由會(huì)員分享，可在線閱讀，更多相關(guān)《北師大版八年級(jí)下冊(cè)數(shù)學(xué) 1.4角平分線 同步練習(xí)題（10頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

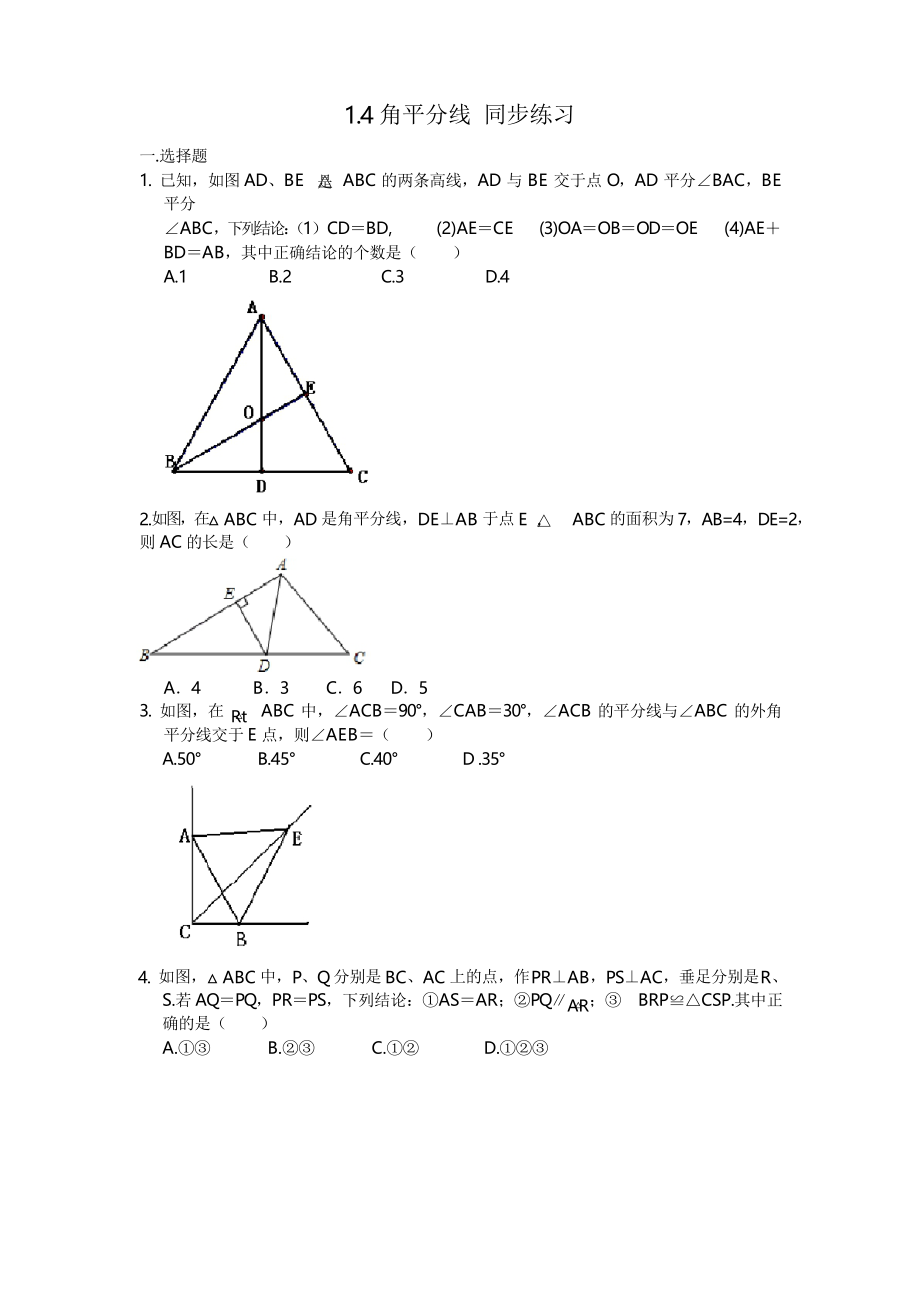
1、 1.4?角平分線?同步練習(xí) 一.選擇題 1.?已知，如圖?AD、BE? ABC?的兩條高線，AD?與?BE?交于點(diǎn)?O，AD?平分∠BAC，BE 平分 ∠ABC，下列結(jié)論：（1）CD＝BD, (2)AE＝CE (3)OA＝OB＝OD＝OE (4)AE＋ BD＝AB，其中正確結(jié)論的個(gè)數(shù)是（ ） A.1 B.2 C.3 D.4 2.如圖，在△?ABC?中，AD?是角平分線，DE⊥AB?于點(diǎn)?E?ABC?的面積為?7，AB=4，DE=2， 則?AC?的長是（ ）

2、 A．4 B．3 C．6 D．5 3.?如圖，在? ABC?中，∠ACB＝90°，∠CAB＝30°，∠ACB?的平分線與∠ABC?的外角 平分線交于?E?點(diǎn)，則∠AEB＝（ ） A.50° B.45° C.40° D?.35° 4.?如圖，△?ABC?中，P、Q?分別是?BC、AC?上的點(diǎn)，作?PR⊥AB，PS⊥AC，垂足分別是?R、 S.若?AQ＝PQ，PR＝PS，下列結(jié)論：①AS＝AR；②PQ∥；③ BRP≌△CSP.其中正 確的是（ ） A.①③ B.②③ C.①② D.①②③

3、 5.如圖是一塊三角形的草坪，現(xiàn)要在草坪上建一涼亭供大家休息，要使涼亭到草坪三條邊的 距離相等，涼亭的位置應(yīng)選在（ ） A ABC?的三條中線的交點(diǎn) B．△?ABC?三邊的中垂線的交點(diǎn) C ABC?三條高所在直線的交點(diǎn) D ABC?三條角平分線的交點(diǎn) 6?．?DABC?中，AD?是?DBAC?的平分線，且?AB?=?AC?+?CD?.若?DBAC?=?60o，則?DABC 的大小為?（ ） A．?40o B．?60o C．?80o D．1

4、00o 二.填空題 7.?在三角形紙片?ABC?中，∠C＝90°，∠A＝30°，AC＝3.折疊該紙片，使點(diǎn)?A?與點(diǎn)?B?重合， 折痕與?AB、AC?分別相交于點(diǎn)?D?和點(diǎn)?E（如圖），折痕?DE?的長為 . 8.?如圖，已知在?△ABC?中，?DA?=?90°,?AB?=?AC,?CD?平分?DACB?，?DE?^?BC?于?E?，若 BC?=?15cm?，則?△DEB?的周長為 cm?． 9.如圖所示

5、，已知△?ABC?的周長是?20，OB、OC?分別平分∠ABC?和∠ACB，OD⊥BC?于?D， 且?OD=3 ABC?的面積是 ． 10. ABC?中，AD?平分∠BAC，AB=4，AC=2 ABD?的面積為?3 ACD?的面 積為 ． B 11．在數(shù)學(xué)活動(dòng)課上，小明提出這樣一個(gè)問題：∠?＝∠C＝90°，E?是?BC?的中點(diǎn)，DE?平分 ∠ADC，∠CED＝35°，如圖，則∠EAB?是多少度？大家一起熱烈地討論交流，小英第 一個(gè)得出正確答案，是______．

6、 12.?如圖，在△?ABC?中，∠ABC＝100°，∠ACB＝20°，CE?平分∠ACB,D?為?AC?上一點(diǎn)， 若∠CBD＝20°，則∠CED＝__________. 三.解答題 13．已知：如圖，OD?平分∠POQ，在?OP、OQ?邊上取?OA＝OB，點(diǎn)?C?在?OD?上，CM⊥AD 于?M，CN⊥BD?于?N. 求證：CM＝CN． 14.四邊形?ABCD?中，AC?平分∠BAD，CE⊥AB?于?E

7、，∠ADC+∠B=180° 求證：2AE=AB+AD． 15．已知：如圖，在?ΔABC?中，AD? ABC?的角平分線，E、F?分別是?AB、AC?上一點(diǎn)， 并且有∠EDF＋∠EAF＝180°．試判斷?DE?和?DF?的大小關(guān)系并說明理由． 16．已知：如圖，∠B=∠C=90°，M?是?BC?的中點(diǎn)，DM?平分∠ADC． （1）求證：AM?平分∠BAD； （2）試說明線段?DM?與?AM?有怎樣的位置關(guān)系？ （

8、3）線段?CD、AB、AD?間有怎樣的關(guān)系？直接寫出結(jié)果． 17．如圖，在ΔABC?中，∠C＝90°，BD?平分∠ABC，DE⊥AB?于?E，若△BCD?與△BCA?的面積 比為?3∶8，求△ADE?與△BCA?的面積之比． 18.?已知：如圖，ΔABC?的外角∠CBD?和∠BCE?的平分線?BF、CF?交于點(diǎn)?F. 求證：一點(diǎn)?F?必在∠DAE?的平分線上． 參考答案 一.選擇題 1.【答案】C； 【解析】（1

9、）（2）（4）是正確的. 2.【答案】B； 【解析】解：過點(diǎn)?D?作?DF⊥AC?于?F，∵AD? ABC?的角平分線，DE⊥AB， ∴DE=DF=2，∴ ABC=?×4×2+?AC×2=7，解得?AC=3．故選：B． 3.【答案】B； 【解析】可證?EA?是∠CAB?外角平分線.過點(diǎn)?E?作?EF、EM、EN?分別垂直于?CB、AB、 CA，并且交點(diǎn)分別為?F、M、N，所以?EF＝EM＝EN.所以?EA?是∠CAB?的外角 平分線. 4.【答案】C； 【解析】依據(jù)角平分線的判定定理知?AP?平分∠BAC，①正確，因?A

10、Q＝PQ，∠PAQ＝∠APQ ＝∠BAP，所以②正確. 5.【答案】D； 【解析】解：∵涼亭到草坪三條邊的距離相等， ∴涼亭選擇△?ABC?三條角平分線的交點(diǎn)． 故選?D． 6.【答案】A； 【解析】在?AB?邊上截取?AE＝AC，連接?DE，可證△?ACD≌△AED，可推出?CD＝DE＝ BE， 2∠B＝∠C，所以∠B＝40°. 二.填空題 7.?【答案】1； 【解析】由題意設(shè)?DE＝CE＝?x?，BC＝BD＝AD＝?3x?，AE＝2?x?，AC?＝3?x?＝3，?x?＝ 1. 8.?【答案】15； 【解析】BC＝CE＋BE＝AC＋BE＝

11、AB＋BE＝AD＋BD＋BE＝DE＋BD＋BE＝15?cm?. 9.?【答案】30 【解析】解：如圖，連接?OA，過?O?作?OE⊥AB?于?E，OF⊥AC?于?F， ∵OB、OC?分別平分∠ABC?和∠ACB， ∴OE=OF=OD=3， ∵△ABC?的周長是?22，OD⊥BC?于?D，且?OD=3， ∴ ABC=?×AB×OE+?×BC×OD+?×AC×OF =?×（AB+BC+AC）×3 = 20×3=30 10.【答案】?； 【解析】解：過點(diǎn)?D?作?DE⊥AB，DF⊥AC，

12、 íDAOD?=?DBOD ?OD?=?OD ∵AD?平分∠BAC， ∴DE=DF， ∵AB=4 ABD?的面積為?3， ∴ ABD=?AB?DE=?×4×DE=3，解得?DE=?； ∴DF=?， ∵AC=2， ∴ ACD=?AC?DF=?×2×?=?． 故答案為：?． 11.【答案】35°； 【解析】作?EF⊥AD?于?F DCE≌△DFE（HL），再證△?AFE≌△ABE（HL），可得 ∠FEB＝180°－70°＝110°，∠AEB＝55°，∠EAB＝35°. 12.【答案】10°； 【解析】考慮△?BDC?中，?

13、EC?是∠C?的平分線，?EB?是∠B?的外角平分線，?所以?E?是 △?BDC?的一個(gè)旁心，?于是?ED?平分∠BDA.?∠CED?＝?∠ADE?－?∠DCE?＝ 1 1 1 1 ∠ADB?－ ∠DCB?＝ ∠DBC?＝ ×20°＝?10°. 2 2 2 2 三.解答題 13.【解析】 證明：∵OD?平分∠POQ ∴∠AOD＝∠BOD 在△?AOD? BOD?中 ìOA?=?OB ? ? ∴△AOD≌△BOD（SAS） ∴∠ADO＝∠BDO 又∵CM⊥AD?于?M，CN⊥BD?于?N. ∴CM＝CN（角平分線上的點(diǎn)到角兩邊的距離相等）.

14、 14.【解析】 證明：過?C?作?CF⊥AD?于?F， ∵AC?平分∠BAD， ∴∠FAC=∠EAC， ∵CE⊥AB，CF⊥AD， ∴∠DFC=∠CEB=90°， ∴△AFC≌△AEC， ∴AF=AE，CF=CE， ∵∠ADC+∠B=180° ∴∠FDC=∠EBC， ∴△FDC≌△EBC ∴DF=EB， ∴AB+AD=AE+EB+AD=AE+DF+AD=AF+AE=2AE ∴2AE=AB+AD í?DM?=?DN ?DEMD?=?DFND 15.【解析】DE＝DF. 證明：過點(diǎn)?D?作?DM⊥

15、AB?于?M，DN⊥AC?于?N， ∵AD? ABC?的角平分線， ∴DM＝DN ∵∠EDF＋∠EAF＝180°，即∠2＋∠3＋∠4＋∠EAF?＝180° 又∵∠1＋∠2＋∠3＋∠EAF?＝180° ∴∠1＝∠4 在? DEM?與? DFN?中 ìD1?=?D4 ? ? ∴ DEM≌ DFN?（ASA） ∴DE＝DF 16.【解析】 （1）證明：作?ME⊥AD?于?E， ∵M(jìn)C⊥DC，ME⊥DA，MD?平分∠ADC， ∴ME=MC， ∵M(jìn)?為?BC?中點(diǎn)， ∴MB=MC， 又∵M(jìn)E=MC， ∴ME=MB， 又∵M(jìn)E⊥AD，MB⊥A

16、B， ∴AM?平分∠DAB． （2）解：DM⊥AM， 理由是：∵DM?平分∠CDA，AM?平分∠DAB， ∴∠1=∠2，∠3=∠4， ∵DC∥AB， ∴∠CDA+∠BAD=180°， ∴∠1+∠3=90°， ∴∠DMA=180°﹣（∠1+∠3）=90°， 即?DM⊥AM． （3）解：CD+AB=AD， 理由是：∵M(jìn)E⊥AD，MC⊥CD， ∴∠C=∠DEM=90°， 在?Rt△DCM?和?Rt△DEM?中 ∴Rt△DCM≌Rt△DEM（HL）， ∴CD=DE， 同理?AE=AB， ∵AE+DE=AD， ∴CD+AB=AD．

17、 17.【解析】 解：∵∠C＝90°，BD?平分∠ABC，DE⊥AB?于?E ∴DE＝CD 可證?Rt△BCD≌Rt△BED（HL） 設(shè)△BCD?的面積＝△BED?的面積＝3?x?，△BCA?的面積為?8?x?， △ADE?的面積為?8?x?－6?x?＝2?x?， ∴△ADE?與△BCA?的面積之比為?2?x?：8?x?＝1:4． 18.【解析】 證明：過?F?點(diǎn)作?FM⊥AD，F(xiàn)N⊥AE，F(xiàn)P⊥BC ∵ΔABC?的外角∠CBD?和∠BCE?的平分線?BF、CF?交于點(diǎn)?F. ∴FM?＝FP，?FN＝FP（角平分線上的點(diǎn)到角兩邊的距離相等） ∴FM?＝?FN ∴點(diǎn)?F?必在∠DAE?的平分線上.（到角兩邊的距離相等的點(diǎn)在角的平分線上）