《湘教版九年級(jí)下冊(cè)數(shù)學(xué) 第3章達(dá)標(biāo)檢測(cè)卷》由會(huì)員分享，可在線閱讀，更多相關(guān)《湘教版九年級(jí)下冊(cè)數(shù)學(xué) 第3章達(dá)標(biāo)檢測(cè)卷（10頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

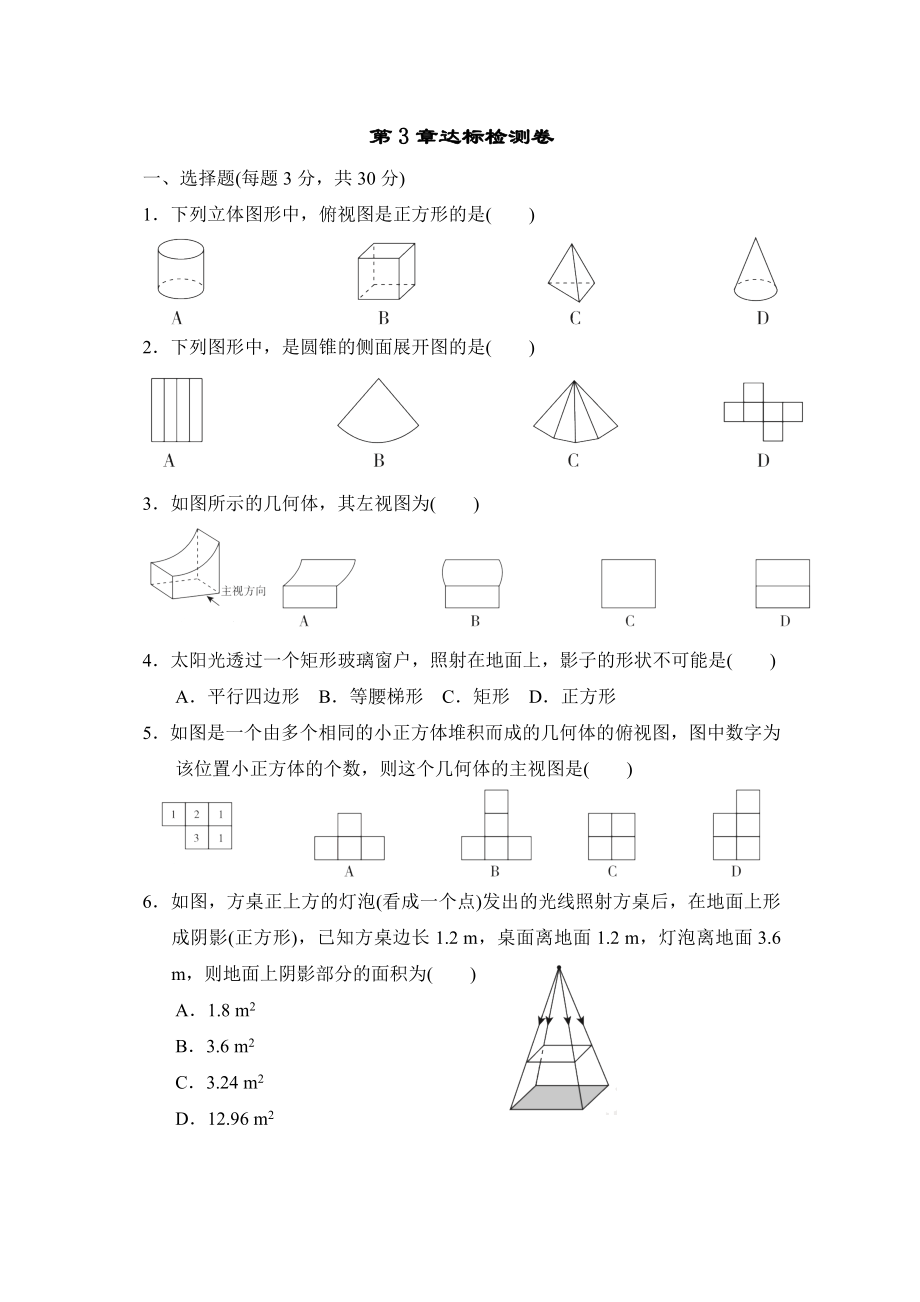
1、第3章達(dá)標(biāo)檢測(cè)卷 一、選擇題(每題3分，共30分) 1．下列立體圖形中，俯視圖是正方形的是(　　) 2．下列圖形中，是圓錐的側(cè)面展開(kāi)圖的是(　　) 3．如圖所示的幾何體，其左視圖為(　　) 4．太陽(yáng)光透過(guò)一個(gè)矩形玻璃窗戶，照射在地面上，影子的形狀不可能是(　　) A．平行四邊形 B．等腰梯形 C．矩形 D．正方形 5．如圖是一個(gè)由多個(gè)相同的小正方體堆積而成的幾何體的俯視圖，圖中數(shù)字為該位置小正方體的個(gè)數(shù)，則這個(gè)幾何體的主視圖是(　　) 6．如圖，方桌正上方的燈泡(看成一個(gè)點(diǎn))發(fā)出的光線照射方桌后，在地面上形成陰影(正方形)，已知方桌邊長(zhǎng)1.2 m，桌面離地

2、面1.2 m，燈泡離地面3.6 m，則地面上陰影部分的面積為(　　) A．1.8 m2 B．3.6 m2 C．3.24 m2 D．12.96 m2 7．已知圓錐的母線長(zhǎng)為3，底面圓的半徑為2，則圓錐的側(cè)面積是(　　) A．4π B．6π C．10π D．12π 8．如圖所示是由若干個(gè)相同的小立方體搭成的幾何體的俯視圖和左視圖，則組成這個(gè)幾何體的小立方體的個(gè)數(shù)可能是(　　) A．5個(gè)或6個(gè) B．5個(gè)或7個(gè) C．4個(gè)、5個(gè)或6個(gè) D．5個(gè)、6個(gè)或7個(gè) 9．在小明家所在的小區(qū)內(nèi)有一條筆直的路，路邊有一盞路燈，一天晚

3、上，小明行走在這條路上，如圖，他從點(diǎn)A走到點(diǎn)B的過(guò)程中，反映他在燈光照射下的影長(zhǎng)l與所走路程s的變化關(guān)系的圖象大致是(　　) 10．某數(shù)學(xué)課外活動(dòng)小組想利用樹(shù)影測(cè)量樹(shù)高，他們?cè)谕粫r(shí)刻測(cè)得一名身高為1.5 m的同學(xué)的影長(zhǎng)為1.35 m．由于大樹(shù)靠近一幢建筑物，因此樹(shù)影的一部分落在建筑物上，如圖，他們測(cè)得地面上的影長(zhǎng)BD為3.6 m，建筑物上的影長(zhǎng)CD為1.8 m，則樹(shù)的高度為(　　) A．5.4 m B．5.8 m C．5.22 m D．6.4 m 二、填空題(每題3分，共24分) 11．在同一時(shí)刻，個(gè)子低的小穎比個(gè)子高的小明身影長(zhǎng)，那么他們此刻是站在__________光下

4、．(填“燈”或“太陽(yáng)”)　 12．如圖所示的這兩個(gè)圖形的正投影分別是________________(不用畫(huà)圖，文字?jǐn)⑹黾纯?． 13．學(xué)校小賣(mài)部的貨架上擺放著某品牌的方便面，它們的三視圖如圖所示，則貨架上的方便面至少有________盒． 14．一個(gè)長(zhǎng)方體的主視圖和左視圖如圖所示(單位：厘米)，則其俯視圖的面積是________平方厘米． 15．如圖，體育課上，甲、乙兩名同學(xué)分別站在C處、D處時(shí)，乙同學(xué)的影子頂端恰好與甲同學(xué)的影子頂端重合，已知甲、乙兩名同學(xué)相距1米，甲同學(xué)身高1.8米，乙同學(xué)身高1.5米，則甲同學(xué)的影長(zhǎng)是________米． 16．如圖是正方體的展開(kāi)圖

5、，則原正方體相對(duì)兩個(gè)面上數(shù)字之和的最小值是________． 17．如圖是一個(gè)幾何體的三視圖，這個(gè)幾何體是________，它的側(cè)面積是________．(結(jié)果保留π) 18．如圖，王華晚上從路燈A的正下方B處走到C處時(shí)，測(cè)得影子CD的長(zhǎng)為1米，繼續(xù)往前走3米到達(dá)E處時(shí)，測(cè)得影子EF的長(zhǎng)為2米，已知王華的身高是1.5米，那么路燈A的高度AB＝______米． 三、解答題(19～21題每題10分，其余每題12分，共66分) 19．在一幢八層樓的樓頂有一個(gè)大燈泡O，該樓房旁邊的樓房A和旗桿C在燈泡下的影子如圖所示，試確定燈泡O的位置，再作出小樹(shù)E在燈泡下的影子FG.(不寫(xiě)作

6、法，保留作圖痕跡) 20．(1)用5個(gè)棱長(zhǎng)為1 cm的小立方塊搭成的幾何體如圖所示，在網(wǎng)格中畫(huà)出它 的三視圖． (2)在實(shí)物圖中，再添加若干個(gè)小立方塊，使得它的左視圖和俯視圖不變，那么最多可添加________個(gè)小立方塊． 21．已知一張正方形紙板ABCD(如圖所示)，其邊長(zhǎng)為20 cm，AD，BC與投影面β平行，AB，CD與投影面β不平行，正方形ABCD在投影面β上的正投影為四邊形A1B1C1D1，若∠ABB1＝45°，求投影四邊形A1B1C1D1的面積． 22．某工廠要制作一批茶葉罐，設(shè)計(jì)者給出了如圖所示的茶葉罐的三視圖，請(qǐng)你按照三視圖確定制作每個(gè)

7、茶葉罐所需鋼板的面積．(圖中單位：mm) 23．如圖，圓錐的底面圓半徑為10 cm，高為10 cm. (1)求圓錐的表面積． (2)若一只螞蟻從底面上一點(diǎn)A出發(fā)繞圓錐一周回到SA上的點(diǎn)M處，且SM＝3AM，求螞蟻所走的最短路徑的長(zhǎng)． 24．某數(shù)學(xué)興趣小組的同學(xué)利用樹(shù)影測(cè)量樹(shù)高，如圖，同學(xué)們已測(cè)出樹(shù)AB的影長(zhǎng)AC為9米，并測(cè)出此時(shí)太陽(yáng)光線與地面成30°角． (1)求樹(shù)AB的高． (2)因水土流失，此時(shí)樹(shù)AB沿太陽(yáng)光線方向倒下，在傾倒過(guò)程中，樹(shù)影長(zhǎng)度發(fā)生了變化，假

8、設(shè)太陽(yáng)光線與地面的夾角保持不變，求樹(shù)影的最大長(zhǎng)度．(計(jì)算結(jié)果精確到0.1米，參考數(shù)據(jù)：≈1.414，≈1.732) 答案 一、1．B　 2．B　 3．D 4．B　點(diǎn)撥：根據(jù)平行投影的特點(diǎn)(在同一時(shí)刻，不同物體的物高和影長(zhǎng)成比例)可知，矩形在陽(yáng)光下的投影的對(duì)邊應(yīng)該是相等的，所以不會(huì)是等腰梯形，故選B. 5．B　 6．C　 7．B 8．D　點(diǎn)撥：由俯視圖易得，最底層有4個(gè)小立方體；由左視圖易得，第二層最多有3個(gè)小立方體，最少有1個(gè)小立方體．那么組成這個(gè)幾何體的小立方體的個(gè)數(shù)可能是5個(gè)、6個(gè)或7個(gè)．故選D. 9．C 10．B　點(diǎn)撥：如圖，分別延長(zhǎng)AC，BD交于點(diǎn)E. ∵B

9、D＝3.6 m，CD＝1.8 m，且同一時(shí)刻測(cè)得一名身高為1.5 m的同學(xué)的影長(zhǎng)為1.35 m， ∴＝，即＝. ∴DE＝1.62 m. ∵CD∥AB，∴＝，即＝. ∴AB＝5.8 m．即樹(shù)的高度為5.8 m. 二、11．燈　 12．圓，長(zhǎng)方形 13．7　點(diǎn)撥：當(dāng)貨架上的方便面盒數(shù)最少時(shí)，如圖所示，圖中數(shù)字表示該位置疊放的方便面盒數(shù)，因此至少有7盒． 14．6　點(diǎn)撥：其俯視圖如圖(單位：厘米)． 15．6　點(diǎn)撥：由題意知△AED∽△ABC， ∴＝，即＝. ∴AD＝5米．∴AC＝CD＋AD＝6(米)， 即甲同學(xué)的影長(zhǎng)是6米． 16．6　點(diǎn)撥：由正方體展開(kāi)圖的特點(diǎn)可知，

10、2和6所在的面是相對(duì)的兩個(gè)面，3和4所在的面是相對(duì)的兩個(gè)面，1和5所在的面是相對(duì)的兩個(gè)面．∵2＋6＝8，3＋4＝7，1＋5＝6，∴原正方體相對(duì)兩個(gè)面上數(shù)字之和的最小值是6. 17．圓錐；2π　18．6 三、19．解：如圖所示． 20．解：(1)如圖所示． (2)2 21．解：過(guò)點(diǎn)A作AH⊥BB1于點(diǎn)H， ∵∠ABB1＝45°， ∴△ABH是等腰直角三角形，∴AH＝AB＝10 cm， ∴A1B1＝AH＝10 cm. 由題意知A1D1＝AD＝20 cm，且四邊形A1B1C1D1為矩形， ∴矩形A1B1C1D1的面積＝A1B1·A1D1＝10 ×20＝200 (cm2

11、)． ∴投影四邊形A1B1C1D1的面積是200 cm2. 22．解：由三視圖可知茶葉罐的形狀為圓柱，并且圓柱的底面圓直徑(2r)為 100 mm，高(h)為150 mm.制作每個(gè)茶葉罐所需鋼板的面積即為該圓柱的表面積，S表＝2πr2＋2πrh＝2π×502＋2π×50×150＝20 000π(mm2)． 故制作每個(gè)茶葉罐所需鋼板的面積為20 000π mm2. 23．解：(1)由題意，可得圓錐的母線SA＝＝40(cm)， 圓錐的側(cè)面展開(kāi)圖(扇形)的弧長(zhǎng)l＝2π·OA＝20π(cm)． ∴S側(cè)＝l·SA＝400π(cm2)， 而S底＝π·AO2＝100π(cm2)． ∴S表＝

12、S側(cè)＋S底＝(400＋100)π＝500π(cm2)， 即圓錐的表面積為500π cm2. (2)沿母線SA將圓錐的側(cè)面展開(kāi)，如圖所示，連接AM，則線段AM的長(zhǎng)就是螞蟻所走的最短路徑的長(zhǎng)． 由(1)知，SA＝40 cm，＝20π cm.設(shè)側(cè)面展開(kāi)圖(扇形)的圓心角為n°， ∵＝20π，∴n＝＝90. ∴∠S＝90°. ∵SA′＝SA＝40 cm，SM＝3A′M，∴SM＝30 cm. 在Rt△ASM中，由勾股定理，得AM＝＝50(cm)． ∴螞蟻所走的最短路徑的長(zhǎng)是50 cm. 24．解：(1)在Rt△ABC中，∠BAC＝90°，∠ACB＝30°， ∵tan∠ACB＝， ∴AB＝AC·tan∠ACB＝9×≈5.2(米)． 故樹(shù)AB的高約為5.2米． (2)如圖，以點(diǎn)A為圓心，以AB長(zhǎng)為半徑作圓弧，當(dāng)太陽(yáng)光線與圓弧相切時(shí)樹(shù)影最長(zhǎng)，設(shè)點(diǎn)D為切點(diǎn)，連接AD，則AD⊥DE.在Rt△ADE中，∠ADE＝90°，∠AED＝30°，∴AE＝2AD≈2×5.2＝10.4(米)．故樹(shù)影的最大長(zhǎng)度約為10.4米．