《人教版八下數(shù)學(xué) 第17章 方法技巧 構(gòu)直角三角形（二）巧構(gòu)特殊角的直角三角形》由會員分享，可在線閱讀，更多相關(guān)《人教版八下數(shù)學(xué) 第17章 方法技巧 構(gòu)直角三角形（二）巧構(gòu)特殊角的直角三角形（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

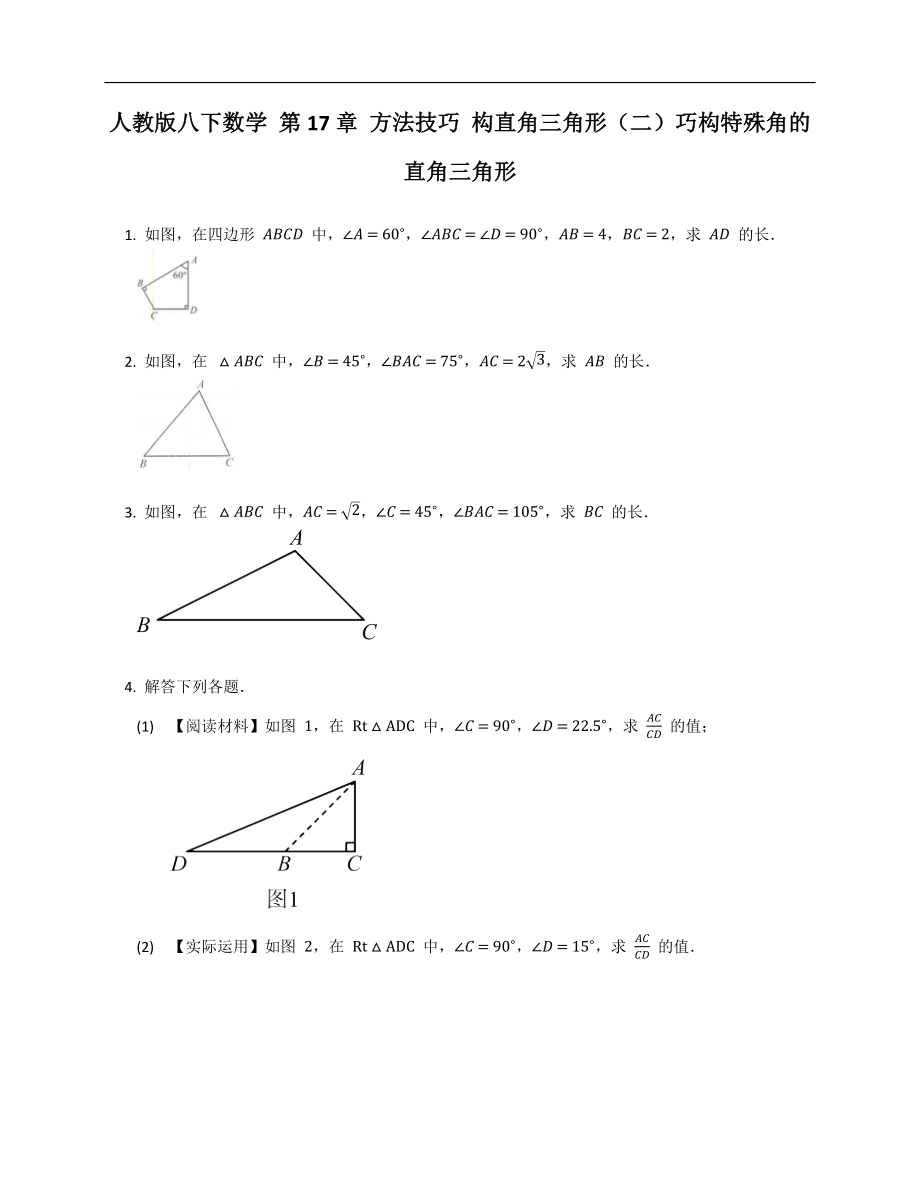
1、 人教版八下數(shù)學(xué) 第17章 方法技巧 構(gòu)直角三角形（二）巧構(gòu)特殊角的直角三角形 1. 如圖，在四邊形 ABCD 中，∠A=60°，∠ABC=∠D=90°，AB=4，BC=2，求 AD 的長． 2. 如圖，在 △ABC 中，∠B=45°，∠BAC=75°，AC=23，求 AB 的長． 3. 如圖，在 △ABC 中，AC=2，∠C=45°，∠BAC=105°，求 BC 的長． 4. 解答下列各題． (1) 【閱讀材料】如圖 1，在 Rt△ADC 中，∠C=90°，∠D=22.5°，求 ACCD 的值； (2) 【實際運用】如圖 2，在 Rt△A

2、DC 中，∠C=90°，∠D=15°，求 ACCD 的值． 答案 1. 【答案】延長 AB，DC 交于點 E， ∵∠D=90°，∠A=60°， ∴∠E=30°， ∴EC=2BC=4，BE=3BC=23， ∴AD=12AE=124+23=2+3． 2. 【答案】過點 A 作 AD⊥BC 于點 D， ∵∠B=45°， ∴∠BAD=45°，∠DAC=30°， ∴CD=12AC=3，AD=AC2-CD2=3， ∵∠B=45°， ∴BD=AD=3， ∴AB=AD2+BD2=32． 3. 【答案】過點 A 作 AD⊥BC 于點 D． ∵

3、∠C=45°， ∴AD=CD， 在 Rt△ACD 中，AD2+CD2=AC2=2， ∴AD=CD=1， 在 Rt△ABD 中，∠BAD=60°，∠B=30°，BA=2AD=2，BD=AB2-AD2=3， ∴BC=BD+CD=3+1． 4. 【答案】 (1) 在 CD 上截取 BC=AC，則 ∠ABC=∠BAC=45°=2∠D， ∴AB=BD， 設(shè) AC=a，則 BC=a，AB=BD=2a， 又 ∵CD=BD+CB=2+1a， ACCD=a2+1a=2-1． (2) 作 AD 的垂直平分線交 CD 于點 B， 則 BD=AB， ∴∠D=∠DAB=15°， ∴∠ABC=∠D+∠DAB=30°， ∵∠C=90°， 故設(shè) AC=x，則 AB=BD=2x，BC=3x， ∴ACCD=x2+3x=2-3．