《浙江省2013年高考數(shù)學(xué)第二輪復(fù)習(xí) 專題升級訓(xùn)練6 導(dǎo)數(shù)及其應(yīng)用 文》由會員分享，可在線閱讀，更多相關(guān)《浙江省2013年高考數(shù)學(xué)第二輪復(fù)習(xí) 專題升級訓(xùn)練6 導(dǎo)數(shù)及其應(yīng)用 文（8頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、專題升級訓(xùn)練6　導(dǎo)數(shù)及其應(yīng)用 (時間：60分鐘　滿分：100分) 一、選擇題(本大題共8小題，每小題5分，共40分) 1．(2012·浙江高考名校交流卷2,8)已知關(guān)于x的函數(shù)f(x)＝－x3＋bx2＋cx＋bc在x＝1處有極值－，則b，c的值是(　　)． A．b＝1，c＝－1，或b＝－1，c＝3 B．b＝1，c＝－1 C．b＝－1，c＝3 D．b＝－1，c＝－1 2．已知函數(shù)f(x)＝x3－3x2＋2在區(qū)間[－1,1]上的最大值與最小值分別為M和m，則M－m＝(　　)． A．1 B．2 C．3 D．4 3．函數(shù)y＝f(x)的圖象在點(diǎn)x＝5處的

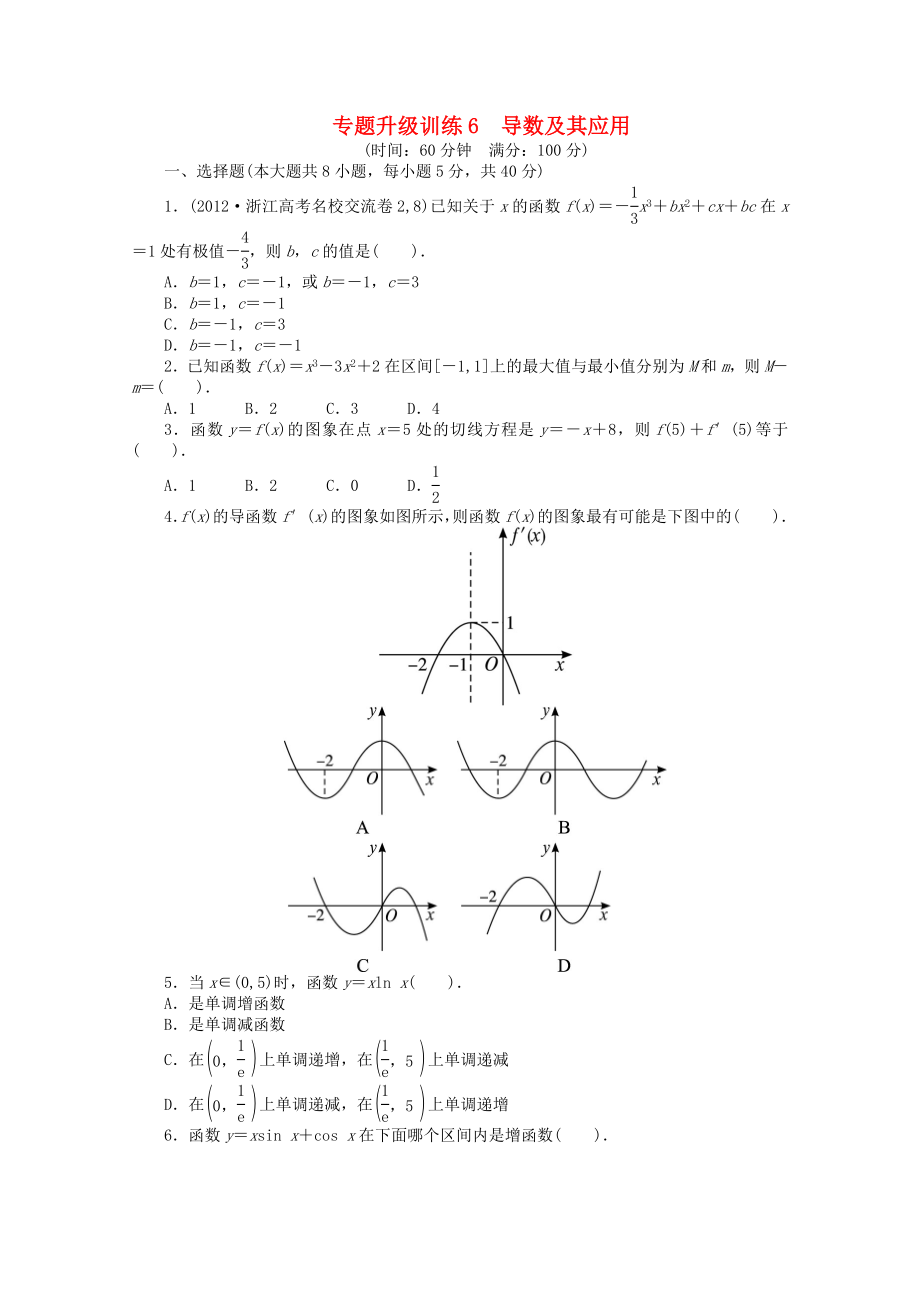
2、切線方程是y＝－x＋8，則f(5)＋f′(5)等于(　　)． A．1 B．2 C．0 D． 4．f(x)的導(dǎo)函數(shù)f′(x)的圖象如圖所示，則函數(shù)f(x)的圖象最有可能是下圖中的(　　)． 5．當(dāng)x∈(0,5)時，函數(shù)y＝xln x(　　)． A．是單調(diào)增函數(shù) B．是單調(diào)減函數(shù) C．在上單調(diào)遞增，在上單調(diào)遞減 D．在上單調(diào)遞減，在上單調(diào)遞增 6．函數(shù)y＝xsin x＋cos x在下面哪個區(qū)間內(nèi)是增函數(shù)(　　)． A． B．(π，2π) C． D．(2π，3π) 7．f(x)是定義在(0，＋∞)上的非負(fù)可導(dǎo)函數(shù)，且滿足

3、xf′(x)－f(x)≤0，對任意正數(shù)a，b，若a＜b，則必有(　　)． A．a(chǎn)f(b)≤bf(a) B．bf(a)≤af(b) C．a(chǎn)f(a)≤f(b) D．bf(b)≤f(a) 8．已知函數(shù)f(x)＝x3＋ax2＋bx＋c，x∈[－2,2]表示的曲線過原點(diǎn)，且在x＝±1處的切線斜率均為－1，給出以下結(jié)論： ①f(x)的解析式為f(x)＝x3－4x，x∈[－2,2]； ②f(x)的極值點(diǎn)有且僅有一個； ③f(x)的最大值與最小值之和等于0. 其中正確的結(jié)論有(　　)． A．0個 B．1個 C．2個 D．3個 二、填空題(本

4、大題共4小題，每小題4分，共16分) 9．在直徑為d的圓木中，截取一個具有最大抗彎強(qiáng)度的長方體梁，則矩形面的長為__________．(強(qiáng)度與bh2成正比，其中h為矩形的長，b為矩形的寬) 10．函數(shù)f(x)＝x3－3a2x＋a(a＞0)的極大值是正數(shù)，極小值是負(fù)數(shù)，則a的取值范圍是__________． 11．若點(diǎn)P是曲線y＝x2－ln x上任意一點(diǎn)，則點(diǎn)P到直線y＝x－2的最小距離為__________． 12．函數(shù)f(x)＝(0＜x＜1)的圖象如圖，M(t，f(t))處的切線為l，l與y軸和直線y＝1分別交于點(diǎn)P，Q，點(diǎn)N(0,1)，若△PQN的面積為b時的點(diǎn)M恰好有兩個，則b的

5、取值范圍為__________． 三、解答題(本大題共4小題，共44分．解答應(yīng)寫出必要的文字說明、證明過程或演算步驟) 13．(本小題滿分10分)設(shè)x＝1與x＝2是函數(shù)f(x)＝aln x＋bx2＋x的兩個極值點(diǎn)． (1)試確定常數(shù)a和b的值； (2)試判斷x＝1，x＝2是函數(shù)f(x)的極大值點(diǎn)還是極小值點(diǎn)，并說明理由． 14．(本小題滿分10分)已知函數(shù)f(x)＝4x3＋3tx2－6t2x＋t－1，x∈R，其中t∈R. (1)當(dāng)t＝1時，求曲線y＝f(x)在點(diǎn)(0，f(0))處的切線方程； (2)當(dāng)t≠0時，求f(x)的單調(diào)區(qū)間． 15．(本小題滿分12分)已知f(x)＝

6、xln x，g(x)＝－x2＋ax－3. (1)求函數(shù)f(x)在[t，t＋2](t＞0)上的最小值； (2)對一切x∈(0，＋∞),2f(x)≥g(x)恒成立，求實數(shù)a的取值范圍； (3)證明：對一切x∈(0，＋∞)，都有l(wèi)n x＞－成立． 16．(本小題滿分12分)已知函數(shù)f(x)＝x3＋bx2＋cx＋d，設(shè)曲線y＝f(x)在與x軸交點(diǎn)處的切線為y＝4x－12，f′(x)為f(x)的導(dǎo)函數(shù)，滿足f′(2－x)＝f′(x)． (1)求f(x)； (2)設(shè)g(x)＝x，m＞0，求函數(shù)g(x)在[0，m]上的最大值； (3)設(shè)h(x)＝lnf′(x)，若對一切x∈[0,1]，不等式h

7、(x＋1－t)＜h(2x＋2)恒成立，求實數(shù)t的取值范圍． 參考答案 一、選擇題 1．C　解析：由得或 當(dāng)b＝1，c＝－1時，f′(x)＝－(x－1)2≤0， 則函數(shù)f(x)無極值，與題意不符． 當(dāng)b＝－1，c＝3時，符合題意，故選C. 2．D　解析：f′(x)＝3x2－6x＝3x(x－2)， 令f′(x)＝0，得x＝0或x＝2(舍去)． 當(dāng)x∈(－1,0)時，f(x)單調(diào)遞增；當(dāng)x∈(0,1)時，f(x)單調(diào)遞減， ∴M＝f(x)max＝f(0)＝2. 又f(－1)＝－2，f(1)＝0， ∴m＝f(x)min＝－2. 綜上，M－m＝2－(－2)＝4.故選D.

8、3．B　解析：由題意知f(5)＝－5＋8＝3，f′(5)＝－1，故f(5)＋f′(5)＝2.故選B. 4．A　解析：根據(jù)導(dǎo)函數(shù)f′(x)的圖象可知f(x)在(－∞，－2)，(0，＋∞)上單調(diào)遞減，在(－2,0)上單調(diào)遞增．故選A. 5．D　解析：y′＝ln x＋1，令y′＝0，得x＝. 在上y′＜0，在上y′＞0， ∴y＝xln x在上單調(diào)遞減， 在上單調(diào)遞增．故選D. 6．C　解析：∵y＝xsin x＋cos x， ∴y′＝(xsin x)′＋(cos x)′＝sin x＋xcos x－sin x＝xcos x， ∴當(dāng)＜x＜時，xcos x＞0，即y′＞0. 故函數(shù)y＝xs

9、in x＋cos x在區(qū)間內(nèi)是增函數(shù)．故選C. 7．A　解析：設(shè)F(x)＝，則F′(x)＝≤0， 故F(x)＝為減函數(shù)． 由0＜a＜b，有≥?af(b)≤bf(a)，故選A. 8．C　解析：∵f(0)＝0，∴c＝0.∵f′(x)＝3x2＋2ax＋b， ∴即 解得a＝0，b＝－4， ∴f(x)＝x3－4x，∴f′(x)＝3x2－4. 令f′(x)＝0得x＝±∈[－2,2]，∴極值點(diǎn)有兩個． ∵f(x)為奇函數(shù)，∴f(x)max＋f(x)min＝0. ∴①③正確，故選C. 二、填空題 9．d　解析：如圖為圓木的橫截面， 由b2＋h2＝d2，∴bh2＝b(d2－b2)．

10、 設(shè)f(b)＝b(d2－b2)，∴f′(b)＝－3b2＋d2. 令f′(b)＝0，又∵b＞0， ∴b＝d，且在上f′(b)＞0，在上f′(b)＜0. ∴函數(shù)f(b)在b＝d處取極大值，也是最大值，即抗彎強(qiáng)度最大，此時長h＝d. 10．　解析：f′(x)＝3x2－3a2＝3(x＋a)(x－a)，由f′(x)＝0得x＝±a，當(dāng)－a＜x＜a時，f′(x)＜0，函數(shù)遞減； 當(dāng)x＞a或x＜－a時，f′(x)＞0，函數(shù)遞增． ∴f(－a)＝－a3＋3a3＋a＞0，且f(a)＝a3－3a3＋a＜0，解得a＞. 11．　解析：過點(diǎn)P作y＝x－2的平行直線，且與曲線y＝x2－ln x相切． 設(shè)

11、P(x0，x02－ln x0)，則有k＝＝2x0－. ∴2x0－＝1， ∴x0＝1或x0＝－(舍去)， ∴P(1,1)，∴d＝＝. 12．　解析：因為f′(x)＝， 則得切線l的方程為y－＝(x－t)，得P，Q(2－t,1)， 從而得b＝(2－t)＝－t＋. 令x＝，則x∈(0,1)， 則轉(zhuǎn)化為關(guān)于x的方程x3－4x2＋4x－4b＝0在區(qū)間(0,1)上有兩個不同的根． 設(shè)g(x)＝x3－4x2＋4x－4b， 則g′(x)＝3x2－8x＋4，故函數(shù)g(x)在區(qū)間上為增函數(shù)，在區(qū)間上為減函數(shù)， 從而有解得＜b＜. 三、解答題 13．解：(1)f′(x)＝＋2bx＋1.

12、由已知?解得 (2)x變化時，f′(x)，f(x)的變化情況如下表： x (0,1) 1 (1,2) 2 (2，＋∞) f′(x) － 0 ＋ 0 － f(x) 極小值 極大值 ∴在x＝1處，函數(shù)f(x)取得極小值； 在x＝2處，函數(shù)f(x)取得極大值－ln 2. 14．解：(1)當(dāng)t＝1時，f(x)＝4x3＋3x2－6x，f(0)＝0，f′(x)＝12x2＋6x－6，f′(0)＝－6，所以曲線y＝f(x)在點(diǎn)(0，f(0))處的切線方程為y＝－6x. (2)f′(x)＝12x2＋6tx－6t2. 令f′(x)＝0，解得x＝－t或x＝.

13、因為t≠0，以下分兩種情況討論： ①若t＜0，則＜－t.當(dāng)x變化時，f′(x)，f(x)的變化情況如下表： x (－t，＋∞) f′(x) ＋ － ＋ f(x) 所以，f(x)的單調(diào)遞增區(qū)間是，(－t，＋∞)；f(x)的單調(diào)遞減區(qū)間是. ②若t＞0，則－t＜. 當(dāng)x變化時，f′(x)，f(x)的變化情況如下表： x (－∞，－t) f′(x) ＋ － ＋ f(x) 所以，f(x)的單調(diào)遞增區(qū)間是(－∞，－t)，；f(x)的單調(diào)遞減區(qū)間是. 15．(1)解：f′(x)＝ln x＋1，則當(dāng)x∈時，f′(x)＜0，f(x

14、)單調(diào)遞減；當(dāng)x∈時，f′(x)＞0，f(x)單調(diào)遞增． ①0＜t＜t＋2＜，沒有最小值； ②0＜t＜＜t＋2，即0＜t＜時，f(x)min＝f＝－； ③≤t＜t＋2，即t≥時，f(x)在[t，t＋2]上單調(diào)遞增，f(x)min＝f(t)＝tln t．所以f(x)min＝ (2)解：2xln x≥－x2＋ax－3，則a≤2ln x＋x＋， 設(shè)h(x)＝2ln x＋x＋(x＞0)，則h′(x)＝. ①x∈(0,1)，h′(x)＜0，h(x)單調(diào)遞減； ②x∈(1，＋∞)，h′(x)＞0，h(x)單調(diào)遞增． 所以h(x)min＝h(1)＝4，對一切x∈(0，＋∞),2f(x)≥g(

15、x)恒成立．所以a≤h(x)min＝4，即a的取值范圍是(－∞，4]． (3)證明：問題等價于證明xln x＞－(x∈(0，＋∞))， 由(1)可知f(x)＝xln x(x∈(0，＋∞))的最小值是－， 當(dāng)且僅當(dāng)x＝時取到． 設(shè)m(x)＝－(x∈(0，＋∞))，則m′(x)＝， 易知m(x)max＝－，當(dāng)且僅當(dāng)x＝1時取到， 從而對一切x∈(0，＋∞)，都有l(wèi)n x＞－成立． 16．解：(1)f′(x)＝x2＋2bx＋c， ∵f′(2－x)＝f′(x)， ∴函數(shù)y＝f′(x)的圖象關(guān)于直線x＝1對稱． ∴b＝－1. ∵直線y＝4x－12與x軸的交點(diǎn)為(3,0)， ∴f(

16、3)＝0，且f′(3)＝4，即9＋9b＋3c＋d＝0，且9＋6b＋c＝4，解得c＝1，d＝－3. 則f(x)＝x3－x2＋x－3. (2)f′(x)＝x2－2x＋1＝(x－1)2， g(x)＝x＝x|x－1|＝ 其圖象如圖所示． 當(dāng)x2－x=時，由x≥1，得， 根據(jù)圖象得： ①當(dāng)0＜m≤時，g(x)的最大值為m－m2； ②當(dāng)＜m≤時，g(x)的最大值為； ③當(dāng)m＞時，g(x)的最大值為m2－m. (3)h(x)=ln(x－1)2=2ln|x－1|，h(x+1－t)=2ln|x－t|，h(2x+2)=2ln|2x+1|， ∵當(dāng)x∈[0,1]時，|2x+1|=2x+1， ∴不等式2ln|x－t|＜2ln|2x+1|恒成立等價于|x－t|＜2x+1且x≠t恒成立， 由|x－t|＜2x+1恒成立，得－x－1＜t＜3x+1恒成立， ∵當(dāng)x∈[0,1]時，3x+1∈[1,4]，－x－1∈[－2，－1]， ∴－1＜t＜1， 又∵當(dāng)x∈[0,1]時，由x≠t恒成立，得t?[0,1]， 因此，實數(shù)t的取值范圍是－1＜t＜0.