《【優(yōu)化設(shè)計(jì)】（福建專版）2015中考數(shù)學(xué)總復(fù)習(xí) 第23課時(shí) 投影與視圖模擬預(yù)測》由會(huì)員分享，可在線閱讀，更多相關(guān)《【優(yōu)化設(shè)計(jì)】（福建專版）2015中考數(shù)學(xué)總復(fù)習(xí) 第23課時(shí) 投影與視圖模擬預(yù)測（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

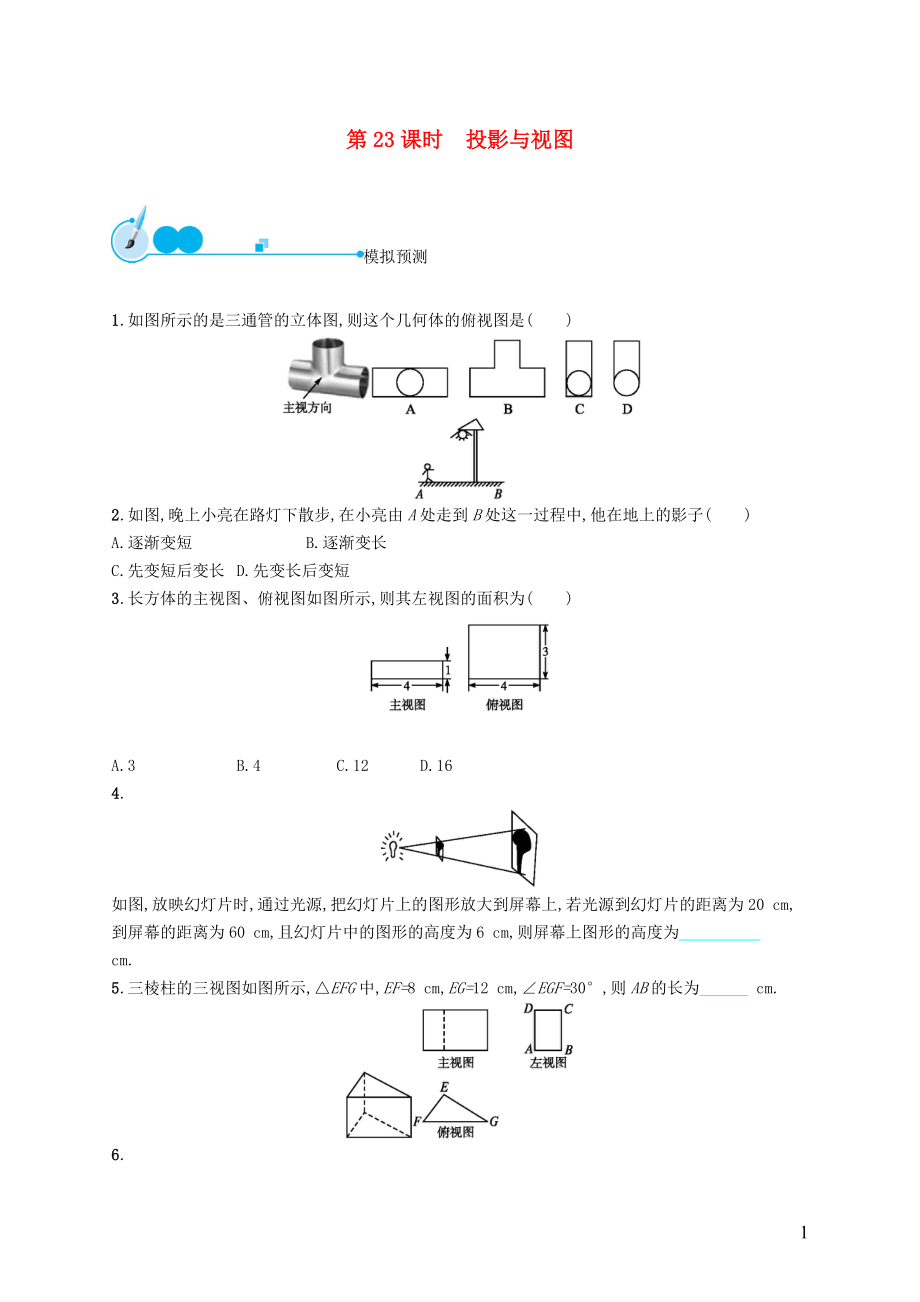
1、 第23課時(shí)　投影與視圖 模擬預(yù)測 1.如圖所示的是三通管的立體圖,則這個(gè)幾何體的俯視圖是(　　) 2.如圖,晚上小亮在路燈下散步,在小亮由A處走到B處這一過程中,他在地上的影子(　　) A.逐漸變短　　　　　　　B.逐漸變長 C.先變短后變長 D.先變長后變短 3.長方體的主視圖、俯視圖如圖所示,則其左視圖的面積為(　　) 　　　　　　　　　　　　　　　　 A.3 B.4 C.12 D.16 4. 如圖,放映幻燈片時(shí),通過光源,把幻燈片上的圖形放大到屏幕上,若光源到幻燈片的距離為20 cm,到屏幕的距離為60 cm,且幻燈片中的圖形的高度為6 c

2、m,則屏幕上圖形的高度為　　　　　 cm.? 5.三棱柱的三視圖如圖所示,△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,則AB的長為　　　 cm.? 6. 如圖是由大小相同的小正方體組成的簡單幾何體的主視圖和左視圖,那么組成這個(gè)幾何體的小正方體的個(gè)數(shù)最多為　　　　　.? 7.小明想利用太陽光測量樓高,他帶著皮尺來到一棟樓下,發(fā)現(xiàn)對面墻上有這棟樓的影子,針對這種情況,他設(shè)計(jì)了一種測量方案,具體測量情況如下: 如示意圖,小明邊移動(dòng)邊觀察,發(fā)現(xiàn)站到點(diǎn)E處時(shí),可以使自己落在墻上的影子與這棟樓落在墻上的影子重疊,且高度恰好相同.此時(shí),測得小明落在墻上的影子高度

3、CD=1.2 m,CE=0.8 m,CA=30 m(點(diǎn)A,E,C在同一直線上).已知小明的身高EF是1.7 m,請你幫小明求出樓高AB.(結(jié)果精確到0.1 m) 答案 1.A　俯視圖是從上向下看得到的圖形. 2.C 3.A　由主視圖可知,這個(gè)長方體的長和高分別是4和1;從俯視圖可知,這個(gè)長方體的長和寬分別是4和3.左視圖看到的長方形的邊長分別是長方體的寬和高,所以左視圖的面積是3×1=3,故選A. 4.18　∵DE∥BC,∴△AED∽△ACB. ∴. 設(shè)屏幕上的小樹高是x cm, 則.解得x=18 cm. 5.6　 根據(jù)三視圖的對應(yīng)情況可得出,△EF

4、G上的高即為AB的長.過點(diǎn)E作EQ⊥FG于點(diǎn)Q.由題意可得出EQ=AB. ∵EG=12 cm,∠EGF=30°,∴AB=EQ=×12=6(cm). 6.7　根據(jù)幾何體的主視圖和左視圖特點(diǎn),推得當(dāng)小正方體最多時(shí)俯視圖如圖所示,所以小正方體最多為7個(gè). 7.解:如圖,過點(diǎn)D作DG⊥AB,分別交AB,EF于點(diǎn)G,H,則 EH=AG=CD=1.2 m, DH=CE=0.8 m,DG=CA=30 m. ∵EF∥AB,∴. 由題意,知FH=EF-EH=1.7-1.2=0.5(m). ∴,解之,得BG=18.75(m). ∴AB=BG+AG=18.75+1.2=19.95≈20.0(m), ∴樓高AB約為20.0 m. 3