《(課標專用 5年高考3年模擬A版)高考數(shù)學(xué) 第二章 函數(shù) 4 指數(shù)和指數(shù)函數(shù)試題 文-人教版高三數(shù)學(xué)試題》由會員分享�����,可在線閱讀����,更多相關(guān)《(課標專用 5年高考3年模擬A版)高考數(shù)學(xué) 第二章 函數(shù) 4 指數(shù)和指數(shù)函數(shù)試題 文-人教版高三數(shù)學(xué)試題(7頁珍藏版)》請在裝配圖網(wǎng)上搜索�����。
1����、指數(shù)和指數(shù)函數(shù)
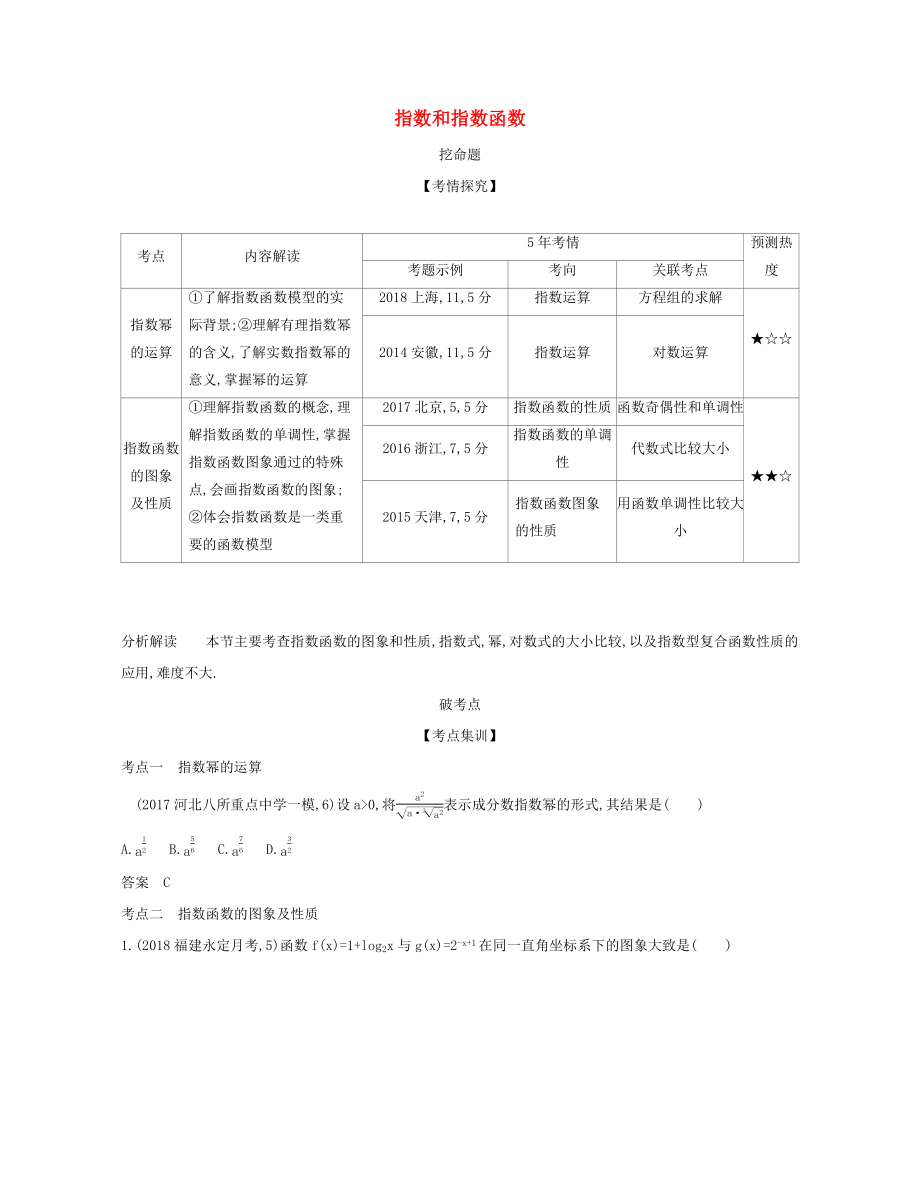
挖命題
【考情探究】
考點
內(nèi)容解讀
5年考情
預(yù)測熱度
考題示例
考向
關(guān)聯(lián)考點
指數(shù)冪
的運算
①了解指數(shù)函數(shù)模型的實際背景;②理解有理指數(shù)冪的含義,了解實數(shù)指數(shù)冪的意義,掌握冪的運算
2018上海,11,5分
指數(shù)運算
方程組的求解
★☆☆
2014安徽,11,5分
指數(shù)運算
對數(shù)運算
指數(shù)函數(shù)
的圖象
及性質(zhì)
①理解指數(shù)函數(shù)的概念,理解指數(shù)函數(shù)的單調(diào)性,掌握指數(shù)函數(shù)圖象通過的特殊點,會畫指數(shù)函數(shù)的圖象;
②體會指數(shù)函數(shù)是一類重要的函數(shù)模型
2017北京,5,5分
指數(shù)函數(shù)的性質(zhì)
函數(shù)奇偶性和單調(diào)性
★★☆
2
2��、016浙江,7,5分
指數(shù)函數(shù)的單調(diào)性
代數(shù)式比較大小
2015天津,7,5分
指數(shù)函數(shù)圖象的性質(zhì)
用函數(shù)單調(diào)性比較大小
分析解讀 本節(jié)主要考查指數(shù)函數(shù)的圖象和性質(zhì),指數(shù)式,冪,對數(shù)式的大小比較,以及指數(shù)型復(fù)合函數(shù)性質(zhì)的應(yīng)用,難度不大.
破考點
【考點集訓(xùn)】
考點一 指數(shù)冪的運算
(2017河北八所重點中學(xué)一模,6)設(shè)a>0,將a2a·3a2表示成分數(shù)指數(shù)冪的形式,其結(jié)果是( )
A.a12 B.a56 C.a76 D.a32
答案 C
考點二 指數(shù)函數(shù)的圖象及性質(zhì)
1.(2
3�����、018福建永定月考,5)函數(shù)f(x)=1+log2x與g(x)=2-x+1在同一直角坐標系下的圖象大致是( )
答案 C
2.(2017廣東深圳一模,6)已知a=0.30.3,b=1.20.3,c=log1.20.3,則a,b,c的大小關(guān)系為( )
A.c(b-1)2 B.ln a>ln b C.a+b>1 D.a
4�、法集訓(xùn)】
方法1 指數(shù)函數(shù)的圖象及其應(yīng)用
(2018廣東潮州期末,6)在我國西北,某地區(qū)荒漠化土地面積每年平均比上一年增長10.4%,專家預(yù)測,經(jīng)過x年可能增長到原來的y倍,則函數(shù)y=f(x)的圖象大致為( )
答案 D
方法2 指數(shù)函數(shù)的性質(zhì)及其應(yīng)用
1.(2018河南八市第一次測評,10)設(shè)函數(shù)f(x)=x2-a與g(x)=ax(a>1且a≠2)在區(qū)間(0,+∞)上具有不同的單調(diào)性,則M=(a-1)0.2與N=1a0.1的大小關(guān)系是( )
A.M=N B.M≤N
5、 C.MN
答案 D
2.(2018福建臺江期末,9)若2x+5y≤2-y+5-x,則有( )
A.x+y≥0 B.x+y≤0 C.x-y≤0 D.x-y≥0
答案 B
3.(2018湖南永州第三次模擬,4)下列函數(shù)中,與函數(shù)y=2x-2-x的定義域�、單調(diào)性與奇偶性均一致的是( )
A.y=sin x B.y=x3
C.y=12x D.y=log2x
答案 B
4.(2017安徽江淮十校第三次聯(lián)考,10)函數(shù)f(x)=x2-bx+c滿足f(x+1)=f(1-x),且f(0)=3,則f(bx)與f(cx)的大小
6、關(guān)系是( )
A. f(bx)≤f(cx) B. f(bx)≥f(cx)
C. f(bx)>f(cx) D.與x有關(guān),不確定
答案 A
過專題
【五年高考】
自主命題·省(區(qū)���、市)卷題組
考點一 指數(shù)冪的運算
1.(2018上海,11,5分)已知常數(shù)a>0,函數(shù)f(x)=2x2x+ax的圖象經(jīng)過點Pp,65�、Qq,-15.若2p+q=36pq,則a= .?
答案 6
2.(2014安徽,11,5分)1681-34+log354+log345= .?
答案 278
考點二 指數(shù)函數(shù)的圖象及性質(zhì)
1.(2017北京,5,5分)已知函數(shù)f(x
7��、)=3x-13x,則f(x)( )
A.是偶函數(shù),且在R上是增函數(shù)
B.是奇函數(shù),且在R上是增函數(shù)
C.是偶函數(shù),且在R上是減函數(shù)
D.是奇函數(shù),且在R上是減函數(shù)
答案 B
2.(2016浙江,7,5分)已知函數(shù)f(x)滿足: f(x)≥|x|且f(x)≥2x,x∈R.( )
A.若f(a)≤|b|,則a≤b B.若f(a)≤2b,則a≤b
C.若f(a)≥|b|,則a≥b D.若f(a)≥2b,則a≥b
答案 B
3.(2015天津,7,5分)已知定義在R上的函數(shù)f(x)=2|x-m
8��、|-1(m為實數(shù))為偶函數(shù).記a=f(log0.53),b=f(log25),c=f(2m),則a,b,c的大小關(guān)系為( )
A.a
9、 )
A.ay3 B.sin x>sin y
C.ln(x2+1)>ln(y2+1) D.1x2+1>1y2+1
答案 A
3.(2015北京,10,5分)2-3,312,log25三個數(shù)中最大的數(shù)是 .?
答案 log25
10���、
【三年模擬】
時間:45分鐘 分值:55分
一���、選擇題(每小題5分,共15分)
1.(2019屆安徽蚌埠重點中學(xué)模擬,2)設(shè)a=40.2,b=30.5,c=30.4,則a,b,c的大小關(guān)系是( )
A.a
11、.-∞,15∪[5,+∞)
答案 C
3.(2017安徽蚌埠二中等四校聯(lián)考,8)定義在R上的偶函數(shù)f(x)滿足:對任意的x1,x2∈(-∞,0)(x1≠x2),都有f(x1)-f(x2)x1-x2<0,則下列結(jié)論正確的是( )
A.f(0.32)
12、 (0,+∞)
5.(2018湖南益陽4月調(diào)研,13)已知函數(shù)f(x)=2x1+a·2x(a∈R)的圖象關(guān)于點0,12對稱,則a= .?
答案 1
三���、解答題(共30分)
6.(2019屆陜西西安高新區(qū)第一中學(xué)模擬,19)已知函數(shù)f(x)=2x,g(x)=x2+2ax(-3≤x≤3).
(1)若g(x)在[-3,3]上是單調(diào)函數(shù),求a的取值范圍;
(2)當(dāng)a=-1時,求函數(shù)y=f(g(x))的值域.
解析 (1)易知g(x)=(x+a)2-a2的圖象的對稱軸為x=-a,
∵g(x)在[-3,3]上是單調(diào)函數(shù),
∴-a≥3或-a≤-3,即a≤-3或a≥3.
13����、(2)當(dāng)a=-1時, f(g(x))=2x2-2x(-3≤x≤3),
令u=x2-2x,y=2u,
∵x∈[-3,3],∴u=(x-1)2-1∈[-1,15].
而y=2u是增函數(shù),∴12≤y≤215.
∴函數(shù)y=f(g(x))的值域是12,215.
7.(2018山東濰坊期中,20)已知函數(shù)f(x)=1-42ax+a(a>0,a≠1)且f(0)=0.
(1)求a的值;
(2)若函數(shù)g(x)=(2x+1)·f(x)+k有零點,求實數(shù)k的取值范圍;
(3)當(dāng)x∈(0,1)時, f(x)>m·2x-2恒成立,求實數(shù)m的取值范圍.
解析 (1)對于函數(shù)f(x)=1-42ax+a
14��、(a>0,a≠1),由f(0)=1-42+a=0,得a=2.
(2)由(1)得f(x)=1-42·2x+2=1-22x+1.
若函數(shù)g(x)=(2x+1)·f(x)+k=2x+1-2+k=2x-1+k 有零點,
則函數(shù)y=2x的圖象和直線y=1-k有交點,
∴1-k>0,解得k<1.
(3)當(dāng)x∈(0,1)時, f(x)>m·2x-2恒成立,即1-22x+1>m·2x-2恒成立.
令t=2x,則t∈(1,2),且m<3t-2t(t+1)=3t+1t(t+1)=1t+2t+1.
由于y=1t+2t+1在t∈(1,2)上單調(diào)遞減,
∴1t+2t+1>12+22+1=76,∴m≤76
15���、.
8.(2017湖北百所重點高中聯(lián)考,21)已知函數(shù)f(x)=22x-7-a4x-1(a>0且a≠1).
(1)當(dāng)a=22時,求不等式f(x)<0的解集;
(2)當(dāng)x∈[0,1]時, f(x)<0恒成立,求實數(shù)a的取值范圍.
解析 (1)當(dāng)a=22=2-12時,不等式f(x)<0即22x-7<2-12(4x-1),
所以2x-7<-12(4x-1),解得x<158,
故當(dāng)a=22時,原不等式的解集為-∞,158.
(2)由22x-71,00且a≠1,∴a∈324,1∪(1,128).
 (課標專用 5年高考3年模擬A版)高考數(shù)學(xué) 第二章 函數(shù) 4 指數(shù)和指數(shù)函數(shù)試題 文-人教版高三數(shù)學(xué)試題
(課標專用 5年高考3年模擬A版)高考數(shù)學(xué) 第二章 函數(shù) 4 指數(shù)和指數(shù)函數(shù)試題 文-人教版高三數(shù)學(xué)試題