《高三數(shù)學二輪復習 第1部分 專題4 突破點10 空間幾何體表面積或體積的求解 理-人教高三數(shù)學試題》由會員分享，可在線閱讀，更多相關《高三數(shù)學二輪復習 第1部分 專題4 突破點10 空間幾何體表面積或體積的求解 理-人教高三數(shù)學試題（12頁珍藏版）》請在裝配圖網(wǎng)上搜索。

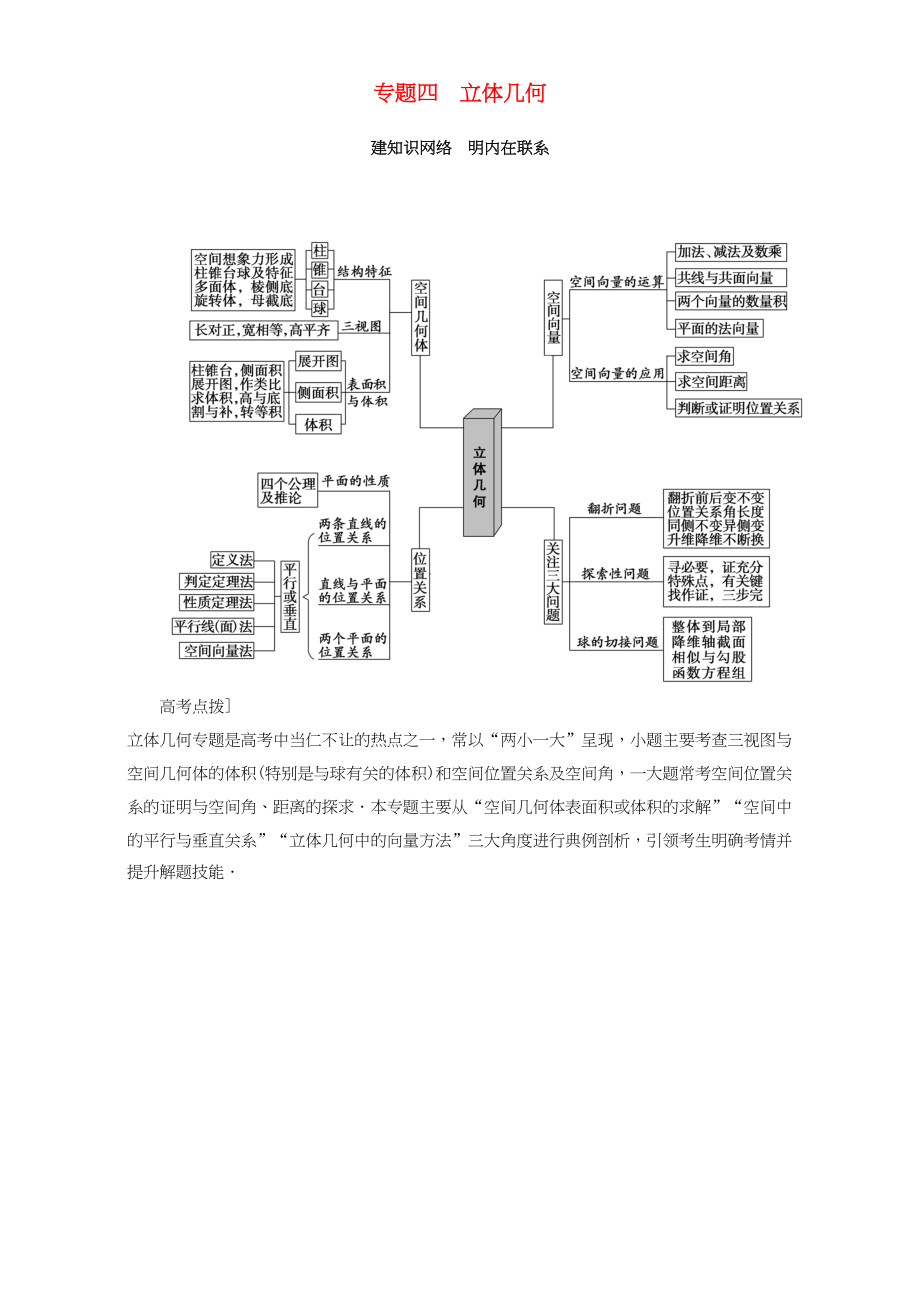
1、專題四　立體幾何 建知識網(wǎng)絡　明內在聯(lián)系 　　　 高考點撥]　立體幾何專題是高考中當仁不讓的熱點之一，常以“兩小一大”呈現(xiàn)，小題主要考查三視圖與空間幾何體的體積(特別是與球有關的體積)和空間位置關系及空間角，一大題?？伎臻g位置關系的證明與空間角、距離的探求．本專題主要從“空間幾何體表面積或體積的求解”“空間中的平行與垂直關系”“立體幾何中的向量方法”三大角度進行典例剖析，引領考生明確考情并提升解題技能． 突破點10　空間幾何體表面積或體積的求解 提煉1 求解幾何體的表面積或體積 (1)對于規(guī)則幾何體，可直接利用公式計算． (2)對于不規(guī)則幾何體，可采用割補法求解；對

2、于某些三棱錐，有時可采用等體積轉換法求解． (3)求解旋轉體的表面積和體積時，注意圓柱的軸截面是矩形，圓錐的軸截面是等腰三角形，圓臺的軸截面是等腰梯形的應用. 提煉2 球與幾何體的外接與內切 (1)正四面體與球：設正四面體的棱長為a ，由正四面體本身的對稱性，可知其內切球和外接球的球心相同，則內切球的半徑r＝a，外接球的半徑R＝a. 圖10-1 (2)正方體與球：設正方體ABCD-A1B1C1D1的棱長為a，O為其對稱中心，E，F(xiàn)，H，G分別為AD，BC，B1C1，A1D1的中點，J為HF的中點，如圖10-1所示． ①正方體的內切球：截面圖為正方形EFHG的內切圓，故其內切球

3、的半徑為OJ＝； ②正方體的棱切球：截面圖為正方形EFHG的外接圓，故其棱切球的半徑為OG＝； ③正方體的外接球：截面圖為矩形ACC1A1的外接圓，故其外接球的半徑為OA1＝. 回訪1　幾何體的表面積或體積 1. (2016·全國甲卷)如圖10-2是由圓柱與圓錐組合而成的幾何體的三視圖，則該幾何體的表面積為(　　) 圖10-2 A．20π B．24π C．28π D．32π C　由三視圖可知圓柱的底面直徑為4，母線長(高)為4，所以圓柱的側面積為2π×2×4＝16π，底面積為π·22＝4π；圓錐的底面直徑為4，高為2，所以圓錐的母線長為＝4，所以圓錐的側面積為π×2×4

4、＝8π.所以該幾何體的表面積為S＝16π＋4π＋8π＝28π.] 2．(2015·全國甲卷)一個正方體被一個平面截去一部分后，剩余部分的三視圖如圖10-3，則截去部分體積與剩余部分體積的比值為(　　) 圖10-3 A.　　　　　　　 B. C.　　　　　　　 D. D　由已知三視圖知該幾何體是由一個正方體截去了一個“大角”后剩余的部分，如圖所示，截去部分是一個三棱錐．設正方體的棱長為1，則三棱錐的體積為 V1＝××1×1×1＝， 剩余部分的體積V2＝13－＝. 所以＝＝，故選D.] 3．(2014·全國卷Ⅱ)如圖10-4，網(wǎng)格紙上正方形小格的邊長為1(表示1 cm)，圖中

5、粗線畫出的是某零件的三視圖，該零件由一個底面半徑為3 cm，高為6 cm的圓柱體毛坯切削得到，則切削掉部分的體積與原來毛坯體積的比值為(　　) 圖10-4 A.　　　　　　　 B. C. D. C　由三視圖可知幾何體是如圖所示的兩個圓柱的組合體．其中左面圓柱的高為4 cm，底面半徑為2 cm，右面圓柱的高為2 cm，底面半徑為3 cm，則組合體的體積V1＝π×22×4＋π×32×2＝16π＋18π＝34π(cm3)，原毛坯體積V2＝π×32×6＝54π(cm3)，則所求比值為＝.] 回訪2　球與幾何體的外接與內切 4．(2015·全國卷Ⅱ)已知A，B是球O的球面上兩點，∠AO

6、B＝90°，C為該球面上的動點．若三棱錐O-ABC體積的最大值為36，則球O的表面積為(　　) A．36π B．64π C．144π D．256π C　如圖，設球的半徑為R，∵∠AOB＝90°，∴S△AOB＝R2. ∵VO-ABC＝VC-AOB，而△AOB面積為定值， ∴當點C到平面AOB的距離最大時，VO-ABC最大， ∴當C為與球的大圓面AOB垂直的直徑的端點時，體積VO-ABC最大為×R2×R＝36， ∴R＝6，∴球O的表面積為4πR2＝4π×62＝144π.故選C.] 5．(2013·全國卷Ⅰ)如圖10-5，有一個水平放置的透明無蓋的正方體容器，容器高8 cm，將一

7、個球放在容器口，再向容器內注水，當球面恰好接觸水面時測得水深為6 cm，如果不計容器厚度，則球的體積為(　　) 圖10-5 A. cm3 B． cm3 C. cm3 D. cm3 A　如圖，作出球的一個截面，則MC＝8－6＝2(cm)，BM＝AB＝×8＝4(cm)．設球的半徑為R cm，則R2＝OM2＋MB2＝(R－2)2＋42，∴R＝5， ∴V球＝π×53＝π(cm3)．] 6．(2012·全國卷)已知三棱錐S-ABC的所有頂點都在球O的球面上，△ABC是邊長為1的正三角形，SC為球O的直徑，且SC＝2，則此棱錐的體積為(　　) A. B． C. D. A　由

8、于三棱錐S-ABC與三棱錐O-ABC底面都是△ABC，O是SC的中點，因此三棱錐S-ABC的高是三棱錐O-ABC高的2倍， 所以三棱錐S-ABC的體積也是三棱錐O-ABC體積的2倍． 在三棱錐O-ABC中，其棱長都是1，如圖所示， S△ABC＝×AB2＝， 高OD＝＝， ∴VS-ABC＝2VO-ABC＝2×××＝.] 熱點題型1　幾何體的表面積或體積 題型分析：解決此類題目，準確轉化是前提，套用公式是關鍵，求解時先根據(jù)條件確定幾何體的形狀，再套用公式求解. 　(1)(2016·全國乙卷)如圖10-6，某幾何體的三視圖是三個半徑相等的圓及每個圓中兩條互相垂直的半徑．若該幾

9、何體的體積是，則它的表面積是(　　) 圖10-6 A．17π　　　　 B．18π C．20π D．28π (2)(2016·全國丙卷)如圖10-7，網(wǎng)格紙上小正方形的邊長為1，粗實線畫出的是某多面體的三視圖，則該多面體的表面積為(　　) 圖10-7 A．18＋36　　　　　 B．54＋18 C．90 D．81 (1)A　(2)B　(1)由幾何體的三視圖可知，該幾何體是一個球體去掉上半球的，得到的幾何體如圖．設球的半徑為R，則πR3－×πR3＝π，解得R＝2.因此它的表面積為×4πR2＋πR2＝17π.故選A. (2)由三視圖可知該幾何體是底面為正方形的斜四棱

10、柱，其中有兩個側面為矩形，另兩個側面為平行四邊形，則表面積為(3×3＋3×6＋3×3)×2＝54＋18.故選B.] 1．求解幾何體的表面積及體積的技巧 (1)求幾何體的表面積及體積問題，可以多角度、多方位地考慮，熟記公式是關鍵所在．求三棱錐的體積，等體積轉化是常用的方法，轉化原則是其高易求，底面放在已知幾何體的某一面上． (2)求不規(guī)則幾何體的體積，常用分割或補形的思想，將不規(guī)則幾何體轉化為規(guī)則幾何體以易于求解． 2．根據(jù)幾何體的三視圖求其表面積與體積的三個步驟 (1)根據(jù)給出的三視圖判斷該幾何體的形狀． (2)由三視圖中的大小標示確定該幾何體的各個度量． (3)套用相應的面

11、積公式與體積公式計算求解． 變式訓練1]　(1)(2016·平頂山二模)某幾何體的三視圖如圖10-8所示，則該幾何體的體積為(　　) A.＋ B．5＋ C．5＋ D.＋ 圖10-8 (2)某幾何體的三視圖(單位：cm)如圖10-9所示，則此幾何體的表面積是(　　) 圖10-9 A．90 cm2 B．129 cm2 C．132 cm2 D．138 cm2 圖10-10 (3)(名師押題)如圖10-10，從棱長為6 cm的正方體鐵皮箱ABCD -A1B1C1D1中分離出來由三個正方形面板組成的幾何圖形．如果用圖示中這樣一個裝置來盛水，那么最多能盛的水的體積

12、為________cm3. (1)D　(2)D　(3)36　(1)由三視圖知該幾何體是由一個長方體，一個三棱錐和一個圓柱組成，故該幾何體的體積為V＝2×1×2＋××1×1×2＋×π×12×2＝＋. (2)該幾何體如圖所示，長方體的長、寬、高分別為6 cm,4 cm,3 cm，直三棱柱的底面是直角三角形，邊長分別為3 cm,4 cm,5 cm，所以表面積S＝2×(4×6＋4×3)＋3×6＋3×3]＋＝99＋39＝138(cm2)． (3)最多能盛多少水，實際上是求三棱錐C1-CD1B1的體積． 又V三棱錐C1-CD1B1＝V三棱錐C-B1C1D1＝××6＝36(cm3)，所以用圖示中

13、這樣一個裝置來盛水，最多能盛36 cm3體積的水．] 熱點題型2　球與幾何體的切、接問題 題型分析：與球有關的表面積或體積求解，其核心本質是半徑的求解，這也是此類問題求解的主線，考生要時刻謹記.先根據(jù)幾何體的三視圖確定其結構特征與數(shù)量特征，然后確定其外接球的球心，進而確定球的半徑，最后代入公式求值即可；也可利用球的性質——球面上任意一點對直徑所張的角為直角，然后根據(jù)幾何體的結構特征構造射影定理求解. 　(1)(2016·南昌二模)一個幾何體的三視圖如圖10-11所示，其中正視圖是正三角形，則該幾何體的外接球的表面積為(　　) 圖10-11 A. B. C. D. (2)(20

14、16·全國丙卷)在封閉的直三棱柱ABC-A1B1C1內有一個體積為V的球．若AB⊥BC，AB＝6，BC＝8，AA1＝3，則V的最大值是(　　) A．4π B． C．6π D. (1)D　(2)B　(1)法一　由三視圖可知，該幾何體是如圖所示的三棱錐S - ABC，其中HS是三棱錐的高，由三視圖可知HS＝2，HA＝HB＝HC＝2，故H為△ABC外接圓的圓心，該圓的半徑為2. 由幾何體的對稱性可知三棱錐S-ABC外接球的球心O在直線HS上，連接OB. 設球的半徑為R，則球心O到△ABC外接圓的距離為OH＝|SH－OS|＝|2－R|， 由球的截面性質可得R＝OB＝＝，解得R＝，所

15、以所求外接球的表面積為4πR2＝4π×＝.故選D. 法二　由三視圖可知，該幾何體是如圖所示的三棱錐S -ABC，其中HS是三棱錐的高，由側視圖可知HS＝2，由正視圖和側視圖可得HA＝HB＝HC＝2. 由幾何體的對稱性可知三棱錐外接球的球心O在HS上，延長SH交球面于點P，則SP就是球的直徑， 由點A在球面上可得SA⊥AP. 又SH⊥平面ABC，所以SH⊥AH. 在Rt△ASH中，SA＝＝＝4. 設球的半徑為R，則SP＝2R， 在Rt△SPA中，由射影定理可得SA2＝SH×SP，即42＝2×2R，解得R＝， 所以所求外接球的表面積為4πR2＝4π×＝.故選D. (2)由題意

16、得要使球的體積最大，則球與直三棱柱的若干面相切．設球的半徑為R.因為△ABC的內切圓半徑為＝2，所以R≤2.又2R≤3，所以R≤，所以Vmax＝π3＝π.故選B.] 解決球與幾何體的切、接問題的關鍵在于確定球的半徑與幾何體的度量之間的關系，這就需要靈活利用球的截面性質以及組合體的截面特征來確定．對于旋轉體與球的組合體，主要利用它們的軸截面性質建立相關數(shù)據(jù)之間的關系；而對于多面體，應抓住多面體的結構特征靈活選擇過球心的截面，把多面體的相關數(shù)據(jù)和球的半徑在截面圖形中體現(xiàn)出來． 變式訓練2]　(1)已知直三棱柱ABC-A1B1C1的6個頂點都在球O 的球面上，若AB＝3，AC＝1，∠BAC＝

17、60°，AA1＝2，則該三棱柱的外接球的體積為(　　) 【導學號：85952037】 A. B． C. D．20π (2)(名師押題)一幾何體的三視圖如圖10-12(網(wǎng)格中每個正方形的邊長為1)，若這個幾何體的頂點都在球O的表面上，則球O的表面積是________． 圖10-12 (1)B　(2)20π　(1)設△A1B1C1的外心為O1，△ABC的外心為O2，連接O1O2，O2B，OB，如圖所示． 由題意可得外接球的球心O為O1O2的中點． 在△ABC中，由余弦定理可得BC2＝AB2＋AC2－2AB×ACcos∠BAC＝32＋12－2×3×1×cos 60°＝7，

18、 所以BC＝. 由正弦定理可得△ABC外接圓的直徑2r＝2O2B＝＝，所以r＝＝. 而球心O到截面ABC的距離d＝OO2＝AA1＝1， 設直三棱柱ABC-A1B1C1的外接球半徑為R，由球的截面性質可得R2＝d2＋r2＝12＋2＝，故R＝， 所以該三棱柱的外接球的體積為V＝R3＝.故選B. (2)由三視圖知該幾何體是一個四棱錐，如圖所示，其底面ABCD是長、寬分別為4和2的矩形，高為2， 且側面SDC與底面ABCD垂直，且頂點S在底面上的射影為該側面上的底面邊的中點．由該幾何體的結構特征知球心在過底面中心O且與底面垂直的直線上，同時在過側面△SDC的外接圓圓心且與側面SDC垂直的直線上．因為△SDC為直角三角形，所以球心就為底面ABCD的中心O，所以外接球的半徑為R＝AC＝，故外接球的表面積為4πR2＝20π.]