《高考數(shù)學(xué)復(fù)習(xí)課件高考數(shù)學(xué)第一輪知識點總復(fù)習(xí)(1)》由會員分享�����,可在線閱讀,更多相關(guān)《高考數(shù)學(xué)復(fù)習(xí)課件高考數(shù)學(xué)第一輪知識點總復(fù)習(xí)(1)(21頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
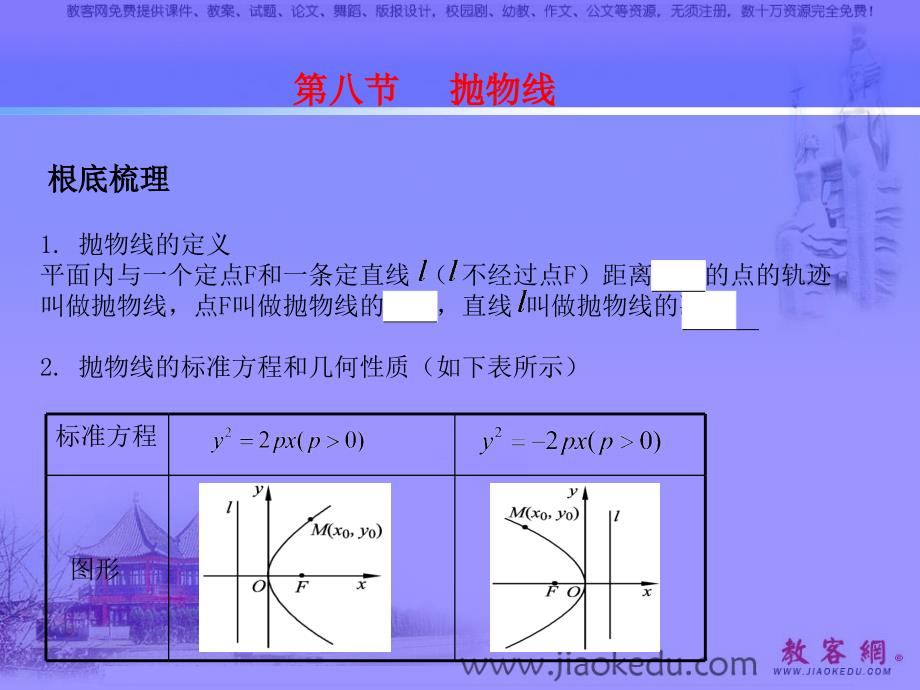
1、單擊此處編輯母版標(biāo)題樣式,單擊此處編輯母版文本樣式,第二級,第三級,第四級,第五級,*,*,*,第八節(jié) 拋物線,根底梳理,標(biāo)準(zhǔn)方程,圖形,1.拋物線的定義,平面內(nèi)與一個定點F和一條定直線(不經(jīng)過點F)距離相等的點的軌跡叫做拋物線�,點F叫做拋物線的焦點,直線 叫做拋物線的準(zhǔn)線.,2.拋物線的標(biāo)準(zhǔn)方程和幾何性質(zhì)(如下表所示),性,質(zhì),范圍,準(zhǔn)線方程,焦點,對稱軸,關(guān)于x軸對稱,頂點,O(0,0),離心率,e=1,標(biāo)準(zhǔn)方程,圖形,性,質(zhì),范圍,準(zhǔn)線方程,焦點,對稱軸,關(guān)于y軸對稱,頂點,O(0�,0),離心率,e=1,典例分析,題型一 拋物線的定義及應(yīng)用,【例1】拋物線 =2x的焦點是F�����,點P是拋物線
2�、上的動點,又有點A,3�����,2�����,求|PA|+|PF|的最小值��,并求出取最小值時P點的坐標(biāo).,分析,拋物線上點P到焦點F的距離等于點P到準(zhǔn)線 的距離d�����,求|PA|+|PF|的問題可轉(zhuǎn)化為|PA|+d的問題,運用三點共線可使問題得到解決.,解,將x=3代入拋物線方程 =2x,得y=.2,點A在拋物線內(nèi)部.,設(shè)拋物線上點P到準(zhǔn)線:x=-的距離為d,由定義,知,|PA|+|PF|=|PA|+d,當(dāng)PA 時�,|PA|+d最小,最小值為 �,即,|PA|+|PF|的最小值為 ,此時P點縱坐標(biāo)為2��,代入 =2x�����,得x=2�,,即點P的坐標(biāo)為(2,2).,學(xué)后反思,靈活地進行拋物線上的點到焦點的距離與到準(zhǔn)線距離的等價
3��、轉(zhuǎn)化�����,是拋物線定義的重要應(yīng)用.,舉一反三,1.假設(shè)例題中點A的坐標(biāo)變?yōu)?�����,3,求|PA|+|PF|的最小值.,解析,將x=2代入拋物線方程,得y=2��,,32,點A在拋物線的外部.,|PA|+|PF|AF|=��,,A�����、P�����、F三點共線時有最小值��,最小值為 .,題型二 拋物線的幾何性質(zhì)和標(biāo)準(zhǔn)方程,【例2】拋物線的頂點在原點��,焦點在坐標(biāo)軸上�,又知此拋物線上的一,點Am,-3到焦點F的距離為5��,求m的值�����,并寫出此拋物線的方程.,分析 因點Am,-3在直線y=-3上��,所以拋物線的開口方向存在向左、向右�、向下三種情況,必須分類討論.,解,(1)若拋物線開口方向向下�,,設(shè)拋物線方程為 =-2py(p0),這時準(zhǔn)
4、線方程為y=,由拋物線定義知 -(-3)=5�����,解得p=4,此時�,拋物線方程為 =-8y.,將點A(m,-3)代入方程,得m=2 .,(2)假設(shè)拋物線開口方向向左或向右��,可設(shè)拋物線方程為 =2ax(a0)��,從p=|a|知準(zhǔn)線方程可統(tǒng)一成x=-的形式�����,于是依題設(shè)有,解此方程組可得四組解,學(xué)后反思,拋物線的標(biāo)準(zhǔn)方程有四種�,在求解過程中,首先要根據(jù)題目描述的幾何性質(zhì)判斷方程形式��,若只能判斷對稱軸�,而不能判斷開口方向,需分情況討論�����,此時,可設(shè)為 =ay(a0)或 =ax(a0)�����,以減少討論次數(shù)和運算量��,然后利用待定系數(shù)法和已知條件求解.,舉一反三,2.拋物線 =2px(p0)有一內(nèi)接直角三角形�����,直角頂點
5�、在原點,一直角邊,的方程是y=2x,斜邊長是5 ,求此拋物線方程.,解析:設(shè)AOB為題中直角三角形��,OA邊所在直線的方程為y=2x,那么OB邊所,在直線的方程為y=-x.,y=2x,由 得 �����;由 得,=2px,那么由|AB|=5 ,得 ,且p0,解得 �����,所求拋物線方程為,題型三 直線與拋物線,【例3】(12分)已知過拋物線 =2px(p0)的焦點F的直線交拋物線于,兩點.,求證:(1)為定值��;(2)為定值.,分析,要證 為定值�,需把直線AB的方程與拋物線方程聯(lián)立,消去y,后�,用韋達(dá)定理求證;要求 為定值,則還要結(jié)合拋物線的,定義來解決問題.,證明,(1)拋物線 =2px的焦點為F(,0)��,當(dāng)直
6�����、線AB的斜率存在,時��,設(shè)直線AB的方程為y=k(x-)(k0).1,y=k(x-),由,=2px,消去y�,整理得,.4,由韋達(dá)定理,得 定值.5,當(dāng)ABx軸時�,也成立6,(2)由拋物線的定義,知,8,(定值)�����,.11,為定值12,學(xué)后反思,解決直線與拋物線位置關(guān)系問題時�,一般要用到根與系數(shù)之間的關(guān)系.,舉一反三,3.若拋物線y=上存在關(guān)于直線:y=-kx+對稱的兩個點M、N��,求k,的取值范圍.,解析,由題意知k0.設(shè) 是拋物線上關(guān)于直線對稱的兩,點��,為其中點,則MN的方程可設(shè)為y=x+b�����,,代入y=�,得 -x-b=0,且=+4b0.,又 ,所以 ,點 在直線:y=-kx+上�����,,將代入,得,或k
7��、0),把點A(-1,1.5)代入方程�����,得,1=2p1.5,即p=�,所以拋物線方程為 ,由點E的縱坐標(biāo)為1��,得點E的橫坐標(biāo),為-�,所以水面EF的寬度為 m.,學(xué)后反思,解決實際問題時建立數(shù)學(xué)模型是關(guān)鍵�,建立適當(dāng)?shù)淖鴺?biāo)系可簡化計算,同時要注意實際背景中的限制條件.,舉一反三,4.如圖�����,汽車前燈反射鏡與軸截面的交線是拋物線的一部分.燈口所在的圓面與反射鏡的軸垂直,燈泡位于拋物線焦點處�����,已知燈口的直徑是24 cm�����,燈深10 cm��,那么燈泡與反射鏡的頂點(即截得拋物線的頂點)距離是多少��?,解析 取反射鏡的軸即拋物線的軸為x軸�����,拋物線的頂點為坐標(biāo)原點�����,建,立直角坐標(biāo)系xOy�,如圖.,燈口直徑|AB|=24
8、 cm�,燈深|OP|=10 cm,點A的坐標(biāo)是10��,12.,設(shè)拋物線的方程為 =2px(p0).,點A10�,12在拋物線上�,得 =2p10,p=7.2.,拋物線焦點F的坐標(biāo)為(3.6,0).,因此,燈泡與反射鏡頂點的距離是3.6 cm.,易錯警示,【例】動點Mx,y)到y(tǒng)軸的距離比它到定點2�����,0的距離小2�,求動點M(x,y)的軌跡方程.,錯解,動點M到y(tǒng)軸的距離比它到定點(2,0)的距離小2�,,動點M到定點(2,0)的距離與到定直線x=-2的距離相等�,,動點M的軌跡是以(2,0)為焦點��,x=-2為準(zhǔn)線的拋物線�,且p=4,,拋物線方程為 =8x��,即M的軌跡方程.,錯解分析 錯解中只求出了在x0的
9��、情況下的M的軌跡方程�,無視了x0的情況.,正解,方法一:(1)當(dāng)x0時,解法同“錯解”�����,得 =8x.,(2)當(dāng)x0時�,由于x軸上原點左側(cè)的點到y(tǒng)軸的距離比它到(2,0),的距離小2,M的軌跡方程為y=0(x0).,綜上��,M的軌跡方程為y=0(x0)和 =8x(x0).,方法二:設(shè)M(x,y)��,那么有|x|+2=,即 +4|x|+4=-4x+4+��,,8x,x0,化簡得 =4x+4|x|=,0,x0),所以 �����,解得2p=25,故方程為 =-25y.,2令x=5�����,那么y=-1.即水位到達(dá)最高點O時��,需 =4小時��;貨車從,接到通知到到達(dá)此橋需 =6(小時��,,因此貨車按原來速度行駛�����,不能平安通過此橋,,要使貨車平安通過此橋�����,速度應(yīng)滿足 .,故速度應(yīng)超過每小時60千米.,
 高考數(shù)學(xué)復(fù)習(xí)課件高考數(shù)學(xué)第一輪知識點總復(fù)習(xí)(1)
高考數(shù)學(xué)復(fù)習(xí)課件高考數(shù)學(xué)第一輪知識點總復(fù)習(xí)(1)