《南昌市10所省重點(diǎn)中學(xué)命制高三第二次模擬突破沖刺（六）文科數(shù)學(xué)試題及答案》由會(huì)員分享，可在線閱讀，更多相關(guān)《南昌市10所省重點(diǎn)中學(xué)命制高三第二次模擬突破沖刺（六）文科數(shù)學(xué)試題及答案（10頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

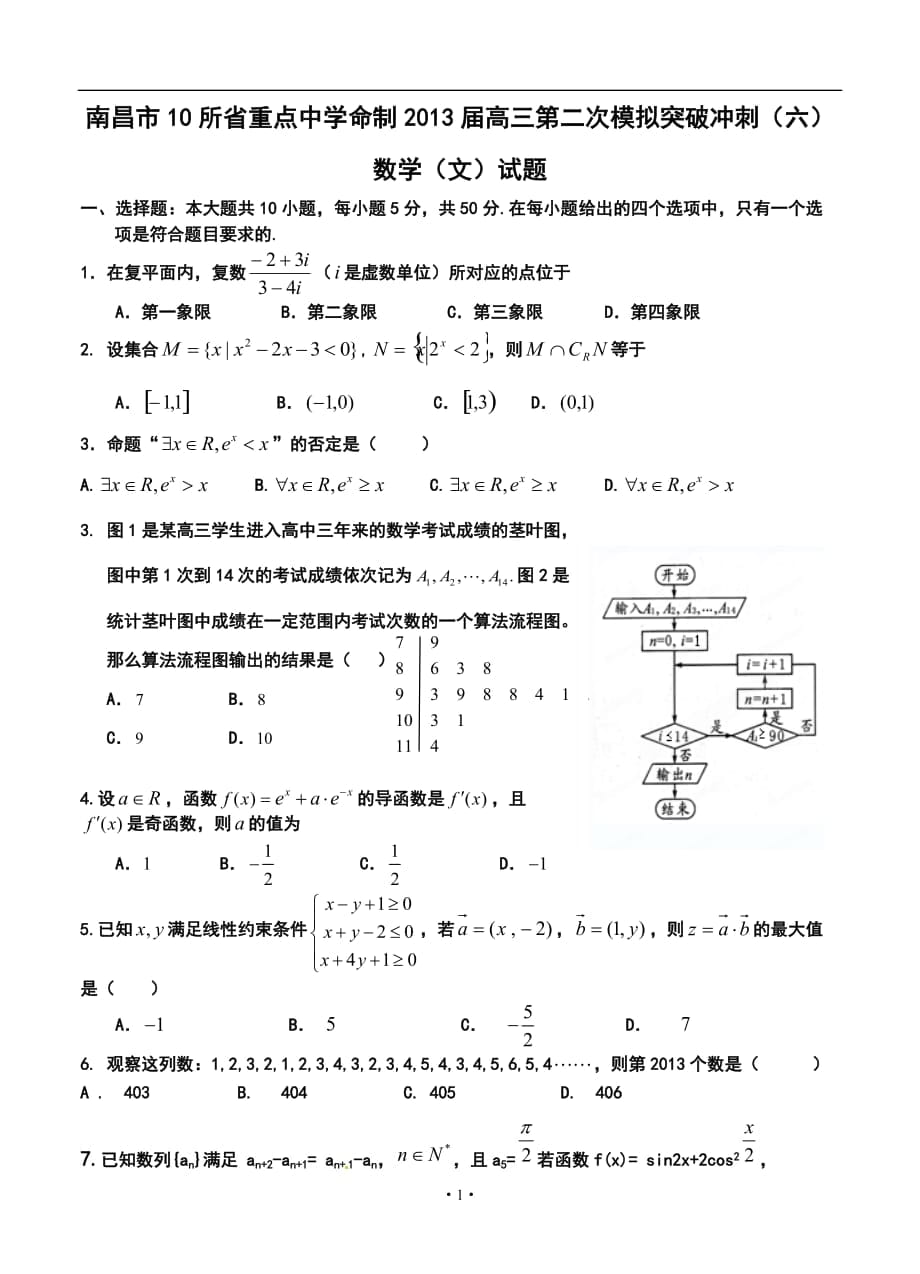
1、 南昌市10所省重點(diǎn)中學(xué)命制2013屆高三第二次模擬突破沖刺（六） 數(shù)學(xué)（文）試題 一、選擇題：本大題共10小題，每小題5分，共50分.在每小題給出的四個(gè)選項(xiàng)中，只有一個(gè)選項(xiàng)是符合題目要求的. 1．在復(fù)平面內(nèi)，復(fù)數(shù)（是虛數(shù)單位）所對(duì)應(yīng)的點(diǎn)位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 2. 設(shè)集合,，則等于 A． B． C． D． 3．命題“”的否定是（ ） A. B. C. D. 3. 7 9 8 6 3 8 9 3 9 8 8 4 1 5 10 3 1 11 4 圖1是某高

2、三學(xué)生進(jìn)入高中三年來(lái)的數(shù)學(xué)考試成績(jī)的莖葉圖，圖中第1次到14次的考試成績(jī)依次記為圖2是統(tǒng)計(jì)莖葉圖中成績(jī)?cè)谝欢ǚ秶鷥?nèi)考試次數(shù)的一個(gè)算法流程圖。那么算法流程圖輸出的結(jié)果是（ ） A． B． C． D． 4.設(shè)，函數(shù)的導(dǎo)函數(shù)是，且是奇函數(shù)，則的值為 A． B． C． D． 5.已知滿足線性約束條件，若，，則的最大值是（ ） A． B． C． D． 6. 觀察這列數(shù)：1,2,3,2,1,2,3,4,3,2,3,

3、4,5,4,3,4,5,6,5,4，則第2013個(gè)數(shù)是（ ） A . 403 B. 404 C. 405 D. 406 7.已知數(shù)列{an}滿足 an+2-an+1= an+1-an，，且a5=若函數(shù)f(x)= sin2x+2cos2， 記yn=f(an)，則數(shù)列{yn}的前9項(xiàng)和為（ ） (A)O (B)-9 (C)9 (D)1 8. 拋物線的焦點(diǎn)為，點(diǎn)在拋物線上，且，弦中點(diǎn)在準(zhǔn)線上的射影為的最大值為( ) A． B． C． D． 10. 如圖，已知正方體的棱長(zhǎng)為1，動(dòng)點(diǎn)P在此

4、正方體的表面上運(yùn)動(dòng)，且，記點(diǎn)P的軌跡的 長(zhǎng)度為，則函數(shù)的圖像可能是（ ） 第Ⅱ卷 二、填空題：本大題有7小題,每小題4分,共28分.把答案填在答題卷的相應(yīng)位置. 20 30 40 50 60 70 歲 頻率/組距 第11題圖 0.0350 0.0125 11.為了“城市品位、方便出行、促進(jìn)發(fā)展”，南昌市擬修建穿江隧道， 市某部門(mén)問(wèn)卷調(diào)查了n個(gè)市民,其中贊成修建穿江隧道的市民占80％， 在贊成修建穿江隧道的市民中又按年齡分組，

5、得樣本頻率分布直方圖 如圖，其中年齡在歲的有400人，歲的有m人， 則n=　　 , m= 12．如圖所示，一個(gè)三棱錐的三視圖是三個(gè)直角三角形 (單位：cm)，則該三棱錐的外接球的表面積為 ______． 第12題圖 13．甲、乙、丙三人站成一排， 其中甲、乙兩人不排在一起的概率為_(kāi)_____________． 14．在ΔABC中，，， 則__________。 15．對(duì)于定義域和值域均為的函數(shù)f(x)，定義，，…，，n=1，2，3，…．滿足的點(diǎn)稱為f的階周期點(diǎn)． 設(shè) 則f的階周期點(diǎn)的個(gè)數(shù)是 4 。 三．解答題：本大題共6小題,滿分75分.解

6、答應(yīng)寫(xiě)出文字說(shuō)明,證明過(guò)程或演算步驟. 16.（本小題滿分12分）已知向量． （1）求的增區(qū)間； （2）已知△ ABC內(nèi)接于半徑為6的圓，內(nèi)角A、B、C的對(duì)邊分別 為，若,求邊長(zhǎng) 17.（本小題滿分12分）已知數(shù)列{}的前項(xiàng)和為 （1）求證：數(shù)列是等比數(shù)列； （2）設(shè)數(shù)列{}的前項(xiàng)和為,求 。 18．（本小題滿分12分）某流感病研究中心對(duì)溫差與甲型H1N1病毒感染數(shù)之間的相關(guān)關(guān)系進(jìn)行研究，他們每天將實(shí)驗(yàn)室放入數(shù)量相同的甲型H1N1病毒和100只白鼠，然后分別記錄了4月1日至4月5日每天晝夜溫差與實(shí)驗(yàn)室里100只白鼠的感染數(shù)，得到如下資料： 日 期 4

7、月1日 4月2日 4月3日 4月4日 4月5日 溫 差 10 13 11 12 7 感染數(shù) 23 32 24 29 17 （1）求這5天的平均感染數(shù)； （2）從4月1日至4月5日中任取2天，記感染數(shù)分別為用的形式列出所有的基本事件, 其中視為同一事件,并求或的概率． 19．（本小題滿分12分）如圖直三棱柱的側(cè)棱長(zhǎng)為，，且，點(diǎn)分別是棱上的動(dòng)點(diǎn)，且. (Ⅰ)求證：無(wú)論在何處，總有 ； (Ⅱ)當(dāng)三棱錐的體積取得最大值時(shí)，求異面直線與所成角的余弦值. 20.（本小題滿分13分）已知處的切線與直線平行。

8、 （1）求滿足的關(guān)系式； （2）若上恒成立，求a的取值范圍； （3）若，數(shù)列滿足求證：. 21. (本小題滿分14分)如圖，直角坐標(biāo)系中，一直角三角形，，B、D在軸上且關(guān)于原點(diǎn)對(duì)稱，在邊上，BD=3DC，△ABC的周長(zhǎng)為12．若一雙曲線以B、C為焦點(diǎn)，且經(jīng)過(guò)A、D兩點(diǎn)． ⑴ 求雙曲線的方程； ⑵ 若一過(guò)點(diǎn)（為非零常數(shù)）的直線與雙曲線相交于不同于雙曲線頂點(diǎn)的兩點(diǎn)、，且，問(wèn)在軸上是否存在定點(diǎn)，使？若存在，求出所有這樣定點(diǎn)的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由 數(shù)學(xué) (文)參考答案 由……1

9、0分 …………12分 17.解：（1）證明：得 當(dāng)≥2時(shí)，由得， 于是， 整理得（≥2）， 所以數(shù)列{}是首項(xiàng)及公比均為的等比數(shù)列?！?分 （2）由（1）得。 于是， 18. 19. 20.解：（1），根據(jù)題意，即 （2）由（Ⅰ）知，， 令， 21．解：(1) 設(shè)雙曲線的方程為，則． 由，得，即． ∴ ………………….3分 解之得，∴． ∴雙曲線的方程為．………………….5分 (2) 設(shè)在軸上存在定點(diǎn)，使． 設(shè)直線的方程為，． 由，得． 即 ① …………6分 ∵，， ∴． 即． ② ………………….8分 把①代入②，得 ③ ………………….9分 10