《河北省中考數(shù)學(xué)總復(fù)習(xí) 專題9圓的有關(guān)計算證明與探究精講試題》由會員分享，可在線閱讀，更多相關(guān)《河北省中考數(shù)學(xué)總復(fù)習(xí) 專題9圓的有關(guān)計算證明與探究精講試題（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、△+△數(shù)學(xué)中考教學(xué)資料2019年編△+△ 專題九　圓的有關(guān)計算、證明與探究 年份 題型 考點 題號 分值 難易度 2017 解答題 切線的性質(zhì)、求扇形的弧長、三角形的外接圓 23 9 中等題 2016 選擇題、解答題 三角形的內(nèi)切圓、外接圓，半圓與點線相切 9、25 3＋10＝13 容易題、較難題 2015 選擇題、解答題 三角形的外接圓、圓與矩形綜合探究 6、26 3＋14＝17 容易題、較難題 命題規(guī)律 河北省對圓的考查獨具匠心，縱觀歷年中考，每年都是原創(chuàng)題，并且出題角度新穎，多以殘缺圓出現(xiàn)，并且把平移、旋轉(zhuǎn)、翻折三種變換融入其中，學(xué)習(xí)

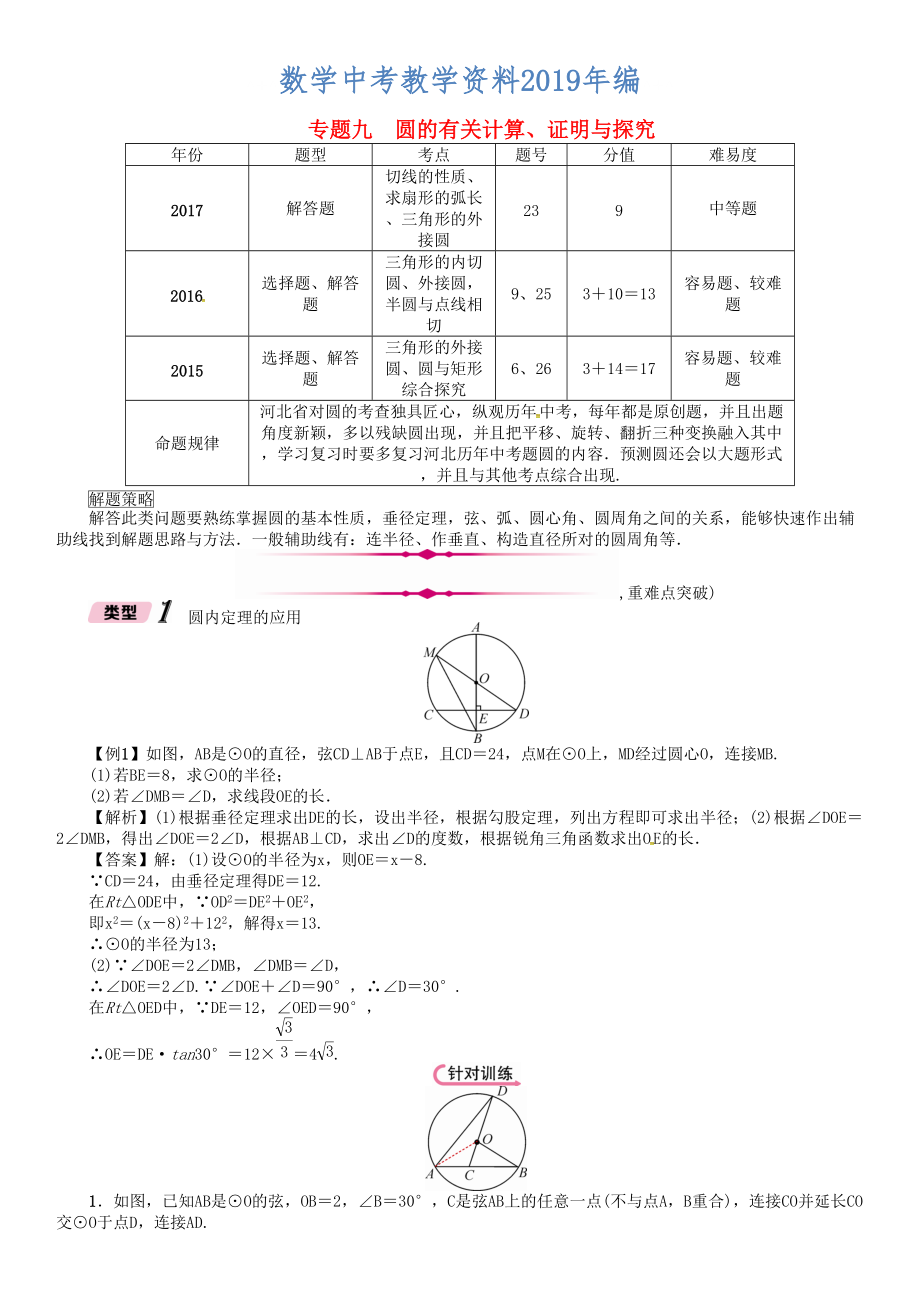
2、復(fù)習(xí)時要多復(fù)習(xí)河北歷年中考題圓的內(nèi)容．預(yù)測圓還會以大題形式，并且與其他考點綜合出現(xiàn). 解答此類問題要熟練掌握圓的基本性質(zhì)，垂徑定理，弦、弧、圓心角、圓周角之間的關(guān)系，能夠快速作出輔助線找到解題思路與方法．一般輔助線有：連半徑、作垂直、構(gòu)造直徑所對的圓周角等． ,重難點突破) 　圓內(nèi)定理的應(yīng)用 【例1】如圖，AB是⊙O的直徑，弦CD⊥AB于點E，且CD＝24，點M在⊙O上，MD經(jīng)過圓心O，連接MB. (1)若BE＝8，求⊙O的半徑； (2)若∠DMB＝∠D，求線段OE的長． 【解析】(1)根據(jù)垂徑定理求出DE的長，設(shè)出半徑，根據(jù)勾股定理，列出方程即可求出半徑；(2)根據(jù)∠D

3、OE＝2∠DMB，得出∠DOE＝2∠D，根據(jù)AB⊥CD，求出∠D的度數(shù)，根據(jù)銳角三角函數(shù)求出OE的長． 【答案】解：(1)設(shè)⊙O的半徑為x，則OE＝x－8. ∵CD＝24，由垂徑定理得DE＝12. 在Rt△ODE中，∵OD2＝DE2＋OE2， 即x2＝(x－8)2＋122，解得x＝13. ∴⊙O的半徑為13； (2)∵∠DOE＝2∠DMB，∠DMB＝∠D， ∴∠DOE＝2∠D.∵∠DOE＋∠D＝90，∴∠D＝30. 在Rt△OED中，∵DE＝12，∠OED＝90， ∴OE＝DEtan30＝12＝4. 1．如圖，已知AB是⊙O的弦，OB＝2，∠B＝30，C是弦AB上的

4、任意一點(不與點A，B重合)，連接CO并延長CO交⊙O于點D，連接AD. (1)弦長AB＝________；(結(jié)果保留根號) (2)當(dāng)∠D＝20時，求∠BOD的度數(shù)； (3)當(dāng)AC的長度為多少時，以A，C，D為頂點的三角形與以B，C，O為頂點的三角形相似？請寫出解答過程． 解：(1)2； (2)連接OA.∵OA＝OB＝OD， ∴∠BAO＝∠B＝30，∠D＝∠DAO＝20， ∴∠DAB＝∠BAO＋∠DAO＝50， ∴∠BOD＝2∠DAB＝100； (3)∵∠BCO＝∠DAC＋∠D， ∴∠BCO>∠DAC，∠BCO>∠D， ∴要使△DAC與△BOC相似，只能∠DCA＝∠BCO

5、＝90， 此時∠BOC＝60，∠BOD＝120， ∴∠DAC＝60，∴△DAC∽△BOC. ∵∠BCO＝90，即OC⊥AB，∴AC＝AB＝. 【方法指導(dǎo)】 熟練掌握圓內(nèi)的4個定理，根據(jù)圖形的形狀和位置選擇合適的定理． 　圓外定理的應(yīng)用 【例2】(天水中考)如圖，點D為⊙O上一點，點C在直徑BA的延長線上，且∠CDA＝∠CBD. (1)判斷直線CD和⊙O的位置關(guān)系，并說明理由； (2)過點B作⊙O的切線BE交直線CD于點E，若AC＝2，⊙O的半徑是3，求BE的長． 【解析】(1)連接OD，根據(jù)圓周角定理求出∠DAB＋∠DBA＝90，從而得出∠CDA＋∠ADO＝90，再根據(jù)

6、切線的判定推出即可；(2)首先利用勾股定理求出DC，由切線長定理得出DE＝EB，在Rt△CBE中根據(jù)勾股定理得出方程，求出方程的解即可． 【答案】解：(1)直線CD和⊙O的位置關(guān)系是相切． 理由：連接OD.∵AB是⊙O的直徑， ∴∠ADB＝90，∴∠DAB＋∠DBA＝90. ∵∠CDA＝∠CBD，∴∠DAB＋∠CDA＝90. ∵OD＝OA，∴∠DAB＝∠ADO， ∴∠CDA＋∠ADO＝90，即OD⊥CE， ∴直線CD是⊙O的切線， 即直線CD和⊙O的位置關(guān)系是相切； (2)∵AC＝2，⊙O的半徑是3，∴OC＝2＋3＝5，OD＝3. 在Rt△CDO中，由勾股定理得CD＝4.

7、 ∵CE切⊙O于點D，EB切⊙O于點B， ∴DE＝EB，∠CBE＝90. 設(shè)DE＝EB＝x， 在Rt△CBE中，由勾股定理，得CE2＝BE2＋BC2， 則(4＋x)2＝x2＋(5＋3)2，解得x＝6，即BE＝6. 2．(畢節(jié)中考)如圖，以△ABC的BC邊上一點O為圓心的圓，經(jīng)過A，B兩點，且與BC邊交于點E，D為BE的下半圓弧的中點，連接AD交BC于點F，AC＝FC. (1)求證：AC是⊙O的切線； (2)已知圓的半徑R＝5，EF＝3，求DF的長． 解：(1)連接AE，AO. ∵BE為直徑，∴∠BAE＝90. ∵＝， ∴∠BAD＝∠EAD＝45， ∴∠AFC＝∠

8、B＋45， ∴∠CAF＝∠EAC＋45. ∵AC＝FC，∴∠AFC＝∠CAF， ∴∠B＋45＝∠EAC＋45，∴∠B＝∠EAC. ∵OA＝OB，∴∠OAB＝∠B，∴∠EAC＝∠OAB， ∴∠OAC＝∠OAE＋∠EAC＝∠OAE＋∠OAB＝∠BAE＝90， ∴AC⊥OA，∴AC為⊙O的切線； (2)連接OD.∵＝， ∴∠BOD＝∠DOE＝90. 在Rt△OFD中 ，OF＝5－3＝2，OD＝5， ∴DF＝＝. 【方法指導(dǎo)】 掌握圓外3個定理和2個定義，了解一種證明方法，熟練應(yīng)用6條輔助線解題． 　圓中的計算 【例3】(2017棗莊中考)如圖，在△ABC中，∠C＝90，∠

9、BAC的平分線交BC于點D，點O在AB上，以點O為圓心，OA為半徑的圓恰好經(jīng)過點D，分別交AC，AB于點E，F(xiàn). (1)試判斷直線BC與⊙O的位置關(guān)系，并說明理由； (2)若BD＝2，BF＝2，求陰影部分的面積．(結(jié)果保留π) 【解析】(1)連接OD，證明OD∥AC，即可證得∠ODB＝90，從而證得BC是圓的切線；(2)在Rt△BOD中，設(shè)OF＝OD＝x，利用勾股定理列出關(guān)于x的方程，求出方程的解得到x的值，即為圓的半徑，求出圓心角的度數(shù)，用Rt△ODB的面積減去扇形DOF的面積即可確定出陰影部分面積． 【答案】解：(1)BC與⊙O相切． 證明：連接OD. ∵AD是∠BAC的平

10、分線， ∴∠BAD＝∠CAD. 又∵OD＝OA， ∴∠OAD＝∠ODA， ∴∠CAD＝∠ODA，∴OD∥AC， ∴∠ODB＝∠C＝90，即OD⊥BC. 又∵BC過半徑OD的外端點D， ∴BC與⊙O相切； (2)設(shè)OF＝OD＝x，則OB＝OF＋BF＝x＋2， 在Rt△BOD中，由勾股定理得：OB2＝OD2＋BD2，即(x＋2)2＝x2＋12， 解得：x＝2，即OD＝OF＝2，∴OB＝2＋2＝4. ∵Rt△ODB中，OD＝OB， ∴∠B＝30，∴∠DOB＝60， ∴S扇形DOF＝＝， ∴S陰影＝S△ODB－S扇形DOF＝22－＝2－. 故陰影部分的面積為2－.

11、 3．(2017襄陽中考)如圖，AB為⊙O的直徑，C，D為⊙O上的兩點，∠BAC＝∠DAC，過點C作直線EF⊥AD，交AD的延長線于點E，連接BC. (1)求證：EF是⊙O的切線； (2)若DE＝1，BC＝2，求劣弧的長l. 解：(1)連接OC. ∵OA＝OC，∴∠OAC＝∠OCA. 又∵∠BAC＝∠DAC， ∴∠DAC＝∠OCA，∴AD∥OC. ∵EF⊥AD，∴EF⊥OC， ∴EF是⊙O的切線； (2)連接OD，DC. ∵∠DAC＝∠DOC， ∠OAC＝∠BOC， ∵∠DAC＝∠OAC. ∴∠DOC＝∠BOC，∴DC＝BC. ∵ED＝1，DC＝BC＝2，∴sin∠ECD＝＝， ∴∠ECD＝30，∴∠OCD＝60. ∵OC＝OD，∴△DOC是等邊三角形， ∴∠BOC＝∠COD＝60，OC＝2， ∴l(xiāng)＝＝. 【方法指導(dǎo)】 熟練應(yīng)用5個公式，關(guān)注與前面知識的綜合應(yīng)用．