《新編高考數(shù)學(xué)二輪復(fù)習(xí) 規(guī)范答題示例10 離散型隨機變量的分布列 理》由會員分享，可在線閱讀，更多相關(guān)《新編高考數(shù)學(xué)二輪復(fù)習(xí) 規(guī)范答題示例10 離散型隨機變量的分布列 理（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

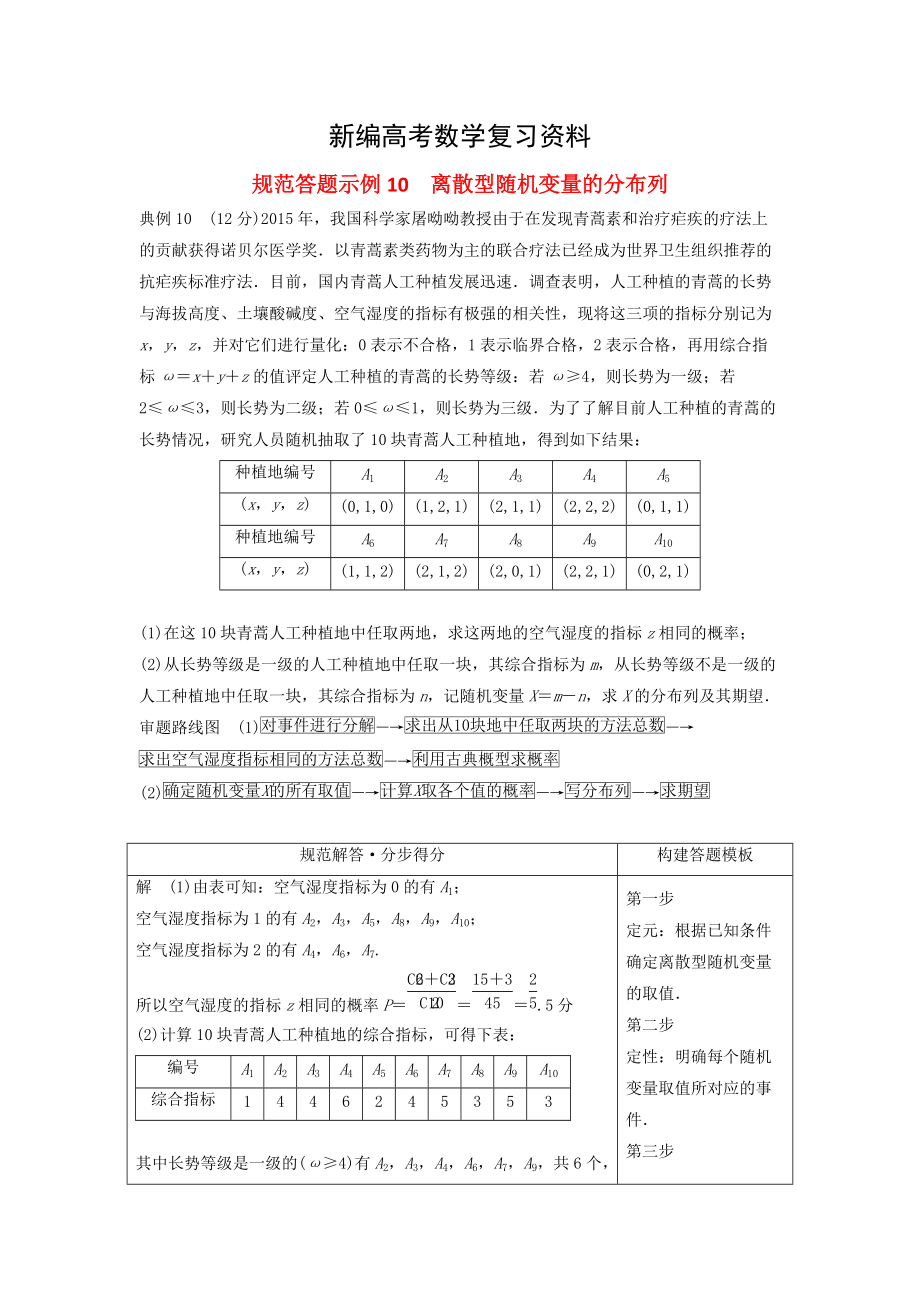
1、新編高考數(shù)學(xué)復(fù)習(xí)資料 規(guī)范答題示例10　離散型隨機變量的分布列 典例10　(12分)2015年，我國科學(xué)家屠呦呦教授由于在發(fā)現(xiàn)青蒿素和治療瘧疾的療法上的貢獻獲得諾貝爾醫(yī)學(xué)獎．以青蒿素類藥物為主的聯(lián)合療法已經(jīng)成為世界衛(wèi)生組織推薦的抗瘧疾標(biāo)準(zhǔn)療法．目前，國內(nèi)青蒿人工種植發(fā)展迅速．調(diào)查表明，人工種植的青蒿的長勢與海拔高度、土壤酸堿度、空氣濕度的指標(biāo)有極強的相關(guān)性，現(xiàn)將這三項的指標(biāo)分別記為x，y，z，并對它們進行量化：0表示不合格，1表示臨界合格，2表示合格，再用綜合指標(biāo)ω＝x＋y＋z的值評定人工種植的青蒿的長勢等級：若ω≥4，則長勢為一級；若2≤ω≤3，則長勢為二級；若0≤ω≤1，則長勢為三級．

2、為了了解目前人工種植的青蒿的長勢情況，研究人員隨機抽取了10塊青蒿人工種植地，得到如下結(jié)果： 種植地編號 A1 A2 A3 A4 A5 (x，y，z) (0,1,0) (1,2,1) (2,1,1) (2,2,2) (0,1,1) 種植地編號 A6 A7 A8 A9 A10 (x，y，z) (1,1,2) (2,1,2) (2,0,1) (2,2,1) (0,2,1) (1)在這10塊青蒿人工種植地中任取兩地，求這兩地的空氣濕度的指標(biāo)z相同的概率； (2)從長勢等級是一級的人工種植地中任取一塊，其綜合指標(biāo)為m，從長勢等級不是一級的人工種植

3、地中任取一塊，其綜合指標(biāo)為n，記隨機變量X＝m－n，求X的分布列及其期望． 審題路線圖　(1)―→―→ ―→ (2)―→―→―→ 規(guī)范解答·分步得分 構(gòu)建答題模板 解　(1)由表可知：空氣濕度指標(biāo)為0的有A1； 空氣濕度指標(biāo)為1的有A2，A3，A5，A8，A9，A10； 空氣濕度指標(biāo)為2的有A4，A6，A7. 所以空氣濕度的指標(biāo)z相同的概率P＝＝＝.5分 (2)計算10塊青蒿人工種植地的綜合指標(biāo)，可得下表： 編號 A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 綜合指標(biāo) 1 4 4 6 2 4 5 3 5 3

4、 其中長勢等級是一級的(ω≥4)有A2，A3，A4，A6，A7，A9，共6個，長勢等級不是一級的(ω<4)有A1，A5，A8，A10，共4個． 隨機變量X的所有可能取值為1,2,3,4,5. P(X＝1)＝＝，P(X＝2)＝＝， P(X＝3)＝＝， P(X＝4)＝＝， P(X＝5)＝＝，10分 所以X的分布列為 X 1 2 3 4 5 P 11分 所以E(X)＝1×＋2×＋3×＋4×＋5×＝.12分 第一步　 定元：根據(jù)已知條件確定離散型隨機變量的取值． 第二步　 定性：明確每個隨機變量取值所對應(yīng)的事件． 第三步　 定型：確定

5、事件的概率模型和計算公式． 第四步　 計算：計算隨機變量取每一個值的概率． 第五步　 列表：列出分布列． 第六步　 求解：根據(jù)公式求期望. 評分細則　(1)第(1)問中，列出空氣濕度相同的情況給2分；計算概率只要式子正確給2分； (2)第(2)問中，列出長勢等級的給2分，只要結(jié)果正確無過程不扣分；計算概率的式子給3分；分布列正確寫出給1分． 跟蹤演練10　(2017·山東)在心理學(xué)研究中，常采用對比試驗的方法評價不同心理暗示對人的影響，具體方法如下：將參加試驗的志愿者隨機分成兩組，一組接受甲種心理暗示，另一組接受乙種心理暗示，通過對比這兩組志愿者接受心理暗示后的結(jié)果來評價

6、兩種心理暗示的作用．現(xiàn)有6名男志愿者A1，A2，A3，A4，A5，A6和4名女志愿者B1，B2，B3，B4，從中隨機抽取5人接受甲種心理暗示，另5人接受乙種心理暗示． (1)求接受甲種心理暗示的志愿者中包含A1但不包含B1的概率； (2)用X表示接受乙種心理暗示的女志愿者人數(shù)，求X的分布列與期望E(X)． 解　(1)記接受甲種心理暗示的志愿者中包含A1但不包含B1的事件為M， 則P(M)＝＝. (2)由題意知X的可能取值為0,1,2,3,4，則 P(X＝0)＝＝， P(X＝1)＝＝， P(X＝2)＝＝， P(X＝3)＝＝， P(X＝4)＝＝. 因此X的分布列為 X 0 1 2 3 4 P 所以X的期望 E(X)＝0×P(X＝0)＋1×P(X＝1)＋2×P(X＝2)＋3×P(X＝3)＋4×P(X＝4)＝0＋1×＋2×＋3×＋4×＝2.