《2018年七年級升八年級數(shù)學(xué) 暑期銜接班講義 第十七講 等邊三角形（拔高）（無答案） 新人教版》由會員分享，可在線閱讀，更多相關(guān)《2018年七年級升八年級數(shù)學(xué) 暑期銜接班講義 第十七講 等邊三角形（拔高）（無答案） 新人教版（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

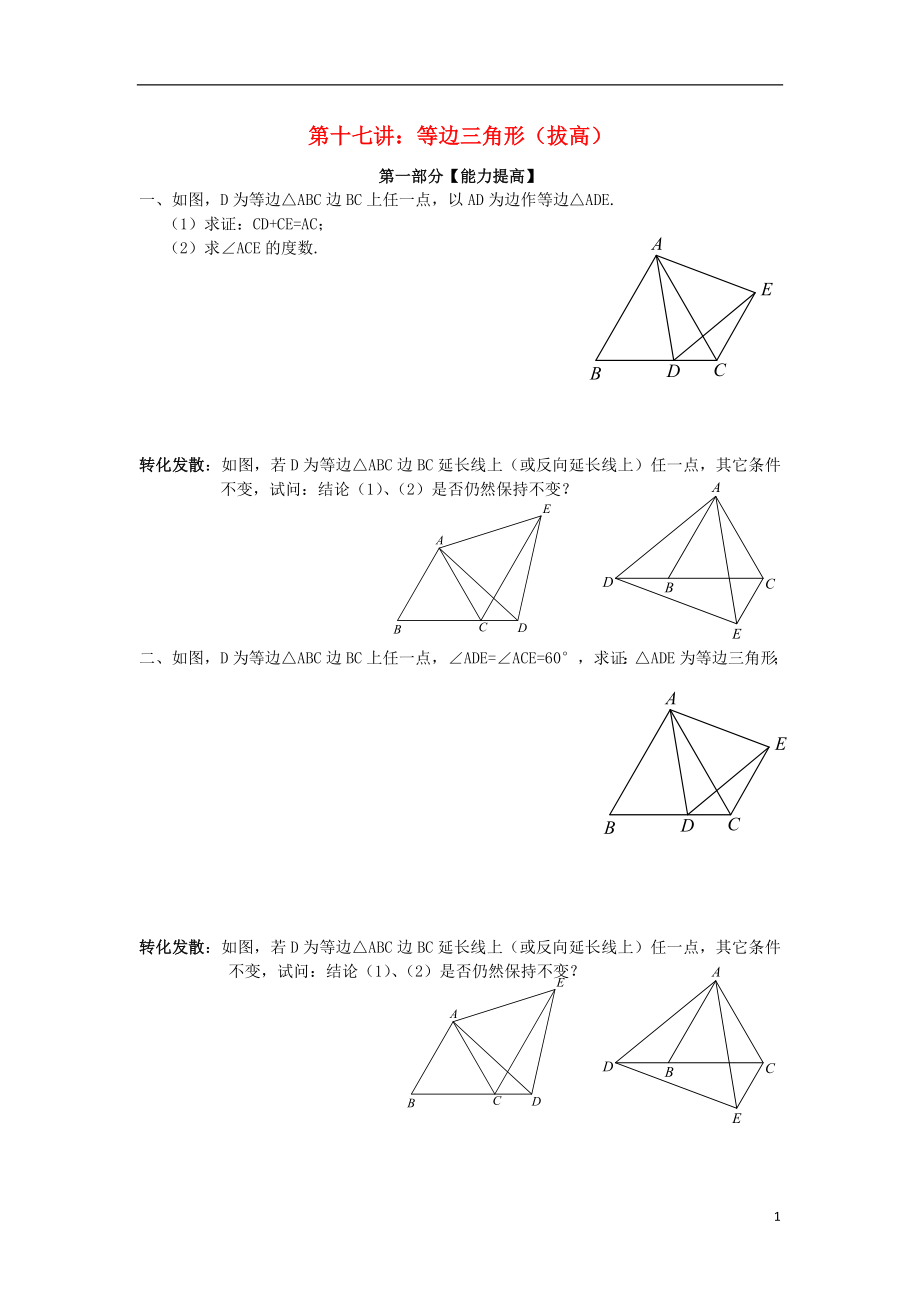
1、 第十七講：等邊三角形（拔高） 第一部分【能力提高】 一、如圖，D為等邊△ABC邊BC上任一點，以AD為邊作等邊△ADE. （1）求證：CD+CE=AC； （2）求∠ACE的度數(shù). 轉(zhuǎn)化發(fā)散：如圖，若D為等邊△ABC邊BC延長線上（或反向延長線上）任一點，其它條件不變，試問：結(jié)論（1）、（2）是否仍然保持不變？ 二、如圖，D為等邊△ABC邊BC上任一點，∠ADE=∠ACE=60°，求證：△ADE為等邊三角形； 轉(zhuǎn)化發(fā)散：如圖，若D為等邊△ABC邊BC延長線上（或反向延長線上）任一

2、點，其它條件不變，試問：結(jié)論（1）、（2）是否仍然保持不變？ 三、如圖，A為線段BC上的一點，AB＞AC，以AB、AC為邊在直線BC的同側(cè)作等邊△ABD、等邊△ACE、連結(jié)DE，以DE為邊向形外作等邊△DEF，點G在AD上，且AG=AE. （1）求證：△EFG≌△GBA； （2）求證：△BDG≌△FGD； 四、 如圖，等邊△ABC中，AB=2，點P是AB邊上的任意一點（點P可以與點A重合，但不與點B重合），過點P作PE⊥BC，垂足為E，過E作EF⊥AC，垂足為F，過點F作

3、FQ⊥AQ，垂足為Q，設(shè)BP=x． （1）請用x的代數(shù)式表示AQ的長度，寫出你的理由； （2）當(dāng)BP的長等于多少時，點P與點Q重合？ 第二部分【綜合運用】 五、如圖，等邊△ABC中，D、E分別在邊BC、AC上，且BD=CE，AD、BE交于F點，連接CF. （1）若CF⊥AD，求證：AF=2BF； （2）連接CF，若AF=2BF，求證：CF⊥AD； 六、如圖，在△ABC中，∠B=45°，D為BC上一點，∠ADC=60°

4、，CD=2BD，求∠C的度數(shù). 七、操作與實驗： 如圖，邊長為1的等邊△ABC，△BCD為頂角為120°的等腰三角形，將一個含30°直角三角板的60°角的頂點放在D點，三角板繞D點旋轉(zhuǎn)，使60°角的兩個夾邊分別交AB、AC于P、Q兩點（三角板的邊足夠長）. 試問: 當(dāng)三角板繞D點旋轉(zhuǎn)時,△APQ的周長是否發(fā)生變化?證明你的結(jié)論； 八、 操作與實驗： 如圖， 已知等邊三角形ABC中，點D，E，F(xiàn)分別為邊AB，AC，BC的中點，M為直線BC上一個動點，以DM為邊作等邊三角形△DMN（點D、M、N為逆時針順序）． （1）如圖

5、1，當(dāng)點M在點B左側(cè)時，請你判斷EN與MF有怎樣的數(shù)量關(guān)系？點F是否在直線NE上？都請直接寫出結(jié)論，不必證明或說明理由； （2）如圖2和圖3，當(dāng)點M在BC上時，其它條件不變，（1）的結(jié)論中EN與MF的數(shù)量關(guān)系是否仍然成立?若成立，請利用圖2或圖3選擇其中的一個證明；若不成立，請說明理由； 九、在△ABC中，∠BAC=60°. ①如圖1，D為AC邊上的一點，以BD為邊作等邊△BDE（點B、D、E按順時針順序），O 為等邊△BDE中∠EBD、∠EDB的角平分線的交點，則∠OAB=________； ②如圖2，D為CA延長線上的一點，

6、以BD為邊作等邊△BDE（點B、D、E按順時針順序），O為等邊△BDE中∠EBD、∠EDB的角平分線的交點，則∠OAB=________； （1）請你完成①②，并選擇其中的一個證明你的結(jié)論； （2）如圖3，D為AC延長線上的一點，以BD為邊作等邊△BDE（點B、D、E按順時針順序），點O為△BDE中與∠EBD、∠EDB相鄰的兩個外角平分線的交點.完成圖3，猜想∠OAB度數(shù)（直接寫出結(jié)論，不需要證明） 十一、如圖，已知C為線段AB上的一點，分別以AC，BC為邊在AB的同側(cè)作等邊△ACD 和等邊△BCE，連接AE，BD交于點O. （1

7、）求證：AE=BD； （2）求∠AOB的度數(shù)； （3）連結(jié)OC，求證：OC平分∠AOB； （4）設(shè)AE、CD交于點P，BD、CE交于點Q，試判斷△CPQ的形狀，并證明你的結(jié)論； （5）求證：OC+OD=OA；（OC+OE=OB） （6）若M、N分別為AE、BD的中點，試判斷△CMN的形狀，并證明你的結(jié)論； 十一、已知：如圖，以△ABC的邊AB、AC為邊，分別在△ABC外作等邊△ABD、等邊△ACE. （1）求證：BE=CD； （2）求∠BOC的度數(shù)；

8、 （3）求證：AO平分∠DOE； （4）求證：①AO+BO=DO；（AO+CO=EO） （5）若P為CD的中點，Q為BE的中點，求證：△APQ為等邊三角形. 十二、如圖，等邊△ABC，動點P從B點出發(fā)，沿射線AB方向運動，同時另一個動點Q從C點出發(fā)，以相同的速度沿射線CA方向運動(當(dāng)Q點到達(dá)A點時運動隨之停止)，連結(jié)PQ交BC于點M. （1）試問：在P、Q兩點的運動過程中，點M與線段PQ是否 存在某種特定的位置關(guān)系？證明你的結(jié)論； （2）如圖，AD⊥BC于點D，過M作MN⊥PQ交AD的延長線于N點.在P、Q兩點的運動時，試問的值是否發(fā)生變化？若不改變，請求出其值；若改變，請說明理由. 7