《2018中考數(shù)學(xué)專題復(fù)習(xí) 動(dòng)態(tài)旋轉(zhuǎn)問(wèn)題試題(無(wú)答案)》由會(huì)員分享�,可在線閱讀,更多相關(guān)《2018中考數(shù)學(xué)專題復(fù)習(xí) 動(dòng)態(tài)旋轉(zhuǎn)問(wèn)題試題(無(wú)答案)(2頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索���。
1�、
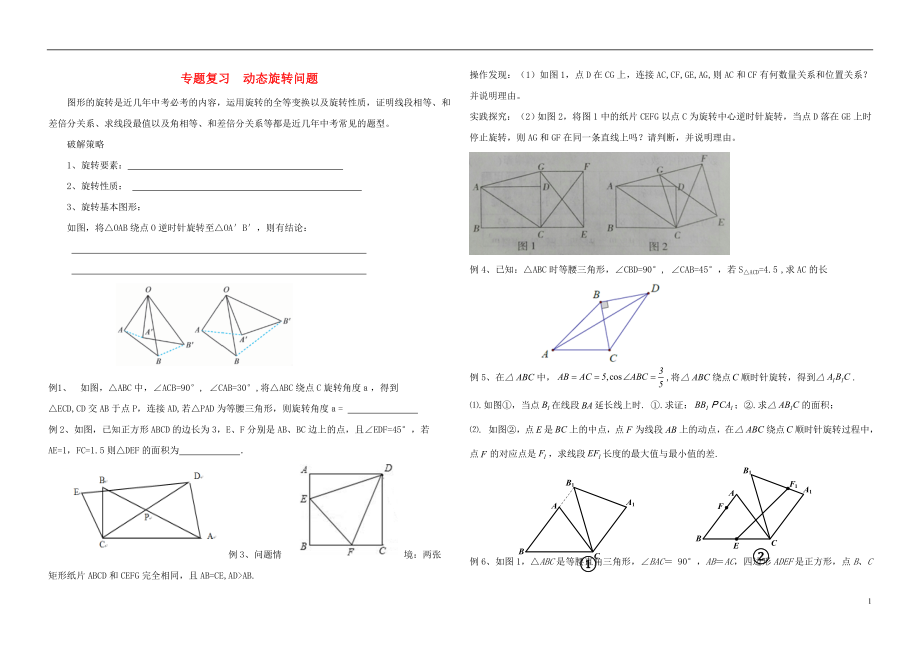
專題復(fù)習(xí) 動(dòng)態(tài)旋轉(zhuǎn)問(wèn)題
圖形的旋轉(zhuǎn)是近幾年中考必考的內(nèi)容��,運(yùn)用旋轉(zhuǎn)的全等變換以及旋轉(zhuǎn)性質(zhì)����,證明線段相等����、和差倍分關(guān)系�����、求線段最值以及角相等�、和差倍分關(guān)系等都是近幾年中考常見(jiàn)的題型。
破解策略
1�、旋轉(zhuǎn)要素:
2、旋轉(zhuǎn)性質(zhì):
3��、旋轉(zhuǎn)基本圖形:
如圖����,將△OAB繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)至△OA′B′,則有結(jié)論:
2�、
例1、 如圖����,△ABC中�,∠ACB=90°, ∠CAB=30°,將△ABC繞點(diǎn)C旋轉(zhuǎn)角度a,得到
△ECD,CD交AB于點(diǎn)P,連接AD,若△PAD為等腰三角形�,則旋轉(zhuǎn)角度a=
例2、如圖��,已知正方形ABCD的邊長(zhǎng)為3�,E、F分別是AB�����、BC邊上的點(diǎn)��,且∠EDF=45°���,若AE=1�,F(xiàn)C=1.5則△DEF的面積為 .
例3���、問(wèn)
3���、題情境:兩張矩形紙片ABCD和CEFG完全相同,且AB=CE,AD>AB.
操作發(fā)現(xiàn):(1)如圖1����,點(diǎn)D在CG上�,連接AC,CF,GE,AG,則AC和CF有何數(shù)量關(guān)系和位置關(guān)系���?并說(shuō)明理由��。
實(shí)踐探究:(2)如圖2�,將圖1中的紙片CEFG以點(diǎn)C為旋轉(zhuǎn)中心逆時(shí)針旋轉(zhuǎn)�����,當(dāng)點(diǎn)D落在GE上時(shí)停止旋轉(zhuǎn)���,則AG和GF在同一條直線上嗎���?請(qǐng)判斷,并說(shuō)明理由����。
例4、已知:△ABC時(shí)等腰三角形����,∠CBD=90°, ∠CAB=45°,若S△ACD=4.5 ,求AC的長(zhǎng)
例5���、在△中�����,,將△繞點(diǎn)順時(shí)針旋轉(zhuǎn)��,得到△.
⑴.如圖①���,當(dāng)點(diǎn)在線段延長(zhǎng)線上時(shí). ①.求證:;②.求△的面積����;
⑵
4、. 如圖②���,點(diǎn)是上的中點(diǎn)����,點(diǎn)為線段上的動(dòng)點(diǎn)�����,在△繞點(diǎn)順時(shí)針旋轉(zhuǎn)過(guò)程中�,點(diǎn)的對(duì)應(yīng)點(diǎn)是��,求線段長(zhǎng)度的最大值與最小值的差.
例6���、如圖1,△ABC是等腰直角三角形��,∠BAC= 90°����,AB=AC,四邊形ADEF是正方形��,點(diǎn)B����、C分別在邊AD、AF上���,此時(shí)BD=CF���,BD⊥CF成立.
(1)當(dāng)△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)θ(0°<θ<90°)時(shí),如圖2�����,BD=CF成立嗎?若成立�,請(qǐng)證明;若不成立����,請(qǐng)說(shuō)明理由.
(2)當(dāng)△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)45°時(shí)�,如圖3,延長(zhǎng)DB交CF于點(diǎn)H.
①求證:BD⊥CF���;
5�、
②當(dāng)AB=2����,AD=3時(shí),求線段DH的長(zhǎng).
例7��、已知:點(diǎn)P是平行四邊形ABCD對(duì)角線AC所在直線上的一個(gè)動(dòng)點(diǎn)(點(diǎn)P不與點(diǎn)A���、C重合)��,分別過(guò)點(diǎn)A�����、C向直線BP作垂線�����,垂足分別為點(diǎn)E��、F����,點(diǎn)O為AC的中點(diǎn).
(1)當(dāng)點(diǎn)P與點(diǎn)O重合時(shí)如圖1,易證OE=OF(不需證明)
(2)直線BP繞點(diǎn)B逆時(shí)針?lè)较蛐D(zhuǎn)�,當(dāng)∠OFE=30°時(shí),如圖2����、圖3的位置,猜想線段CF����、AE、OE之間有怎樣的數(shù)量關(guān)系��?請(qǐng)寫出你對(duì)圖2����、圖3的猜想��,并選擇一種情況給予證明.
例8��、如圖��,在菱形ABCD中���,AB=2,∠BAD=60°�����,過(guò)點(diǎn)D作DE⊥AB于點(diǎn)E�,DF⊥BC于點(diǎn)F.
(1)如圖1���,連接A
6�����、C分別交DE��、DF于點(diǎn)M����、N,求證:MN=AC�;
(2)如圖2,將△EDF以點(diǎn)D為旋轉(zhuǎn)中心旋轉(zhuǎn)�����,其兩邊DE′����、DF′分別與直線AB、BC相交于點(diǎn)G�、P,連接GP���,當(dāng)△DGP的面積等于3時(shí)���,求旋轉(zhuǎn)角的大小并指明旋轉(zhuǎn)方向.
例9、如圖1�,點(diǎn)O是正方形ABCD兩對(duì)角線的交點(diǎn),分別延長(zhǎng)OD到點(diǎn)G�,OC到點(diǎn)E,使OG=2OD��,OE=2OC,然后以O(shè)G�、OE為鄰邊作正方形OEFG,連接AG����,DE.
(1)求證:DE⊥AG����;
(2)正方形ABCD固定,將正方形OEFG繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)α角(0°<α<360°)得到正方形OE′F′G′�,如圖2.①在旋轉(zhuǎn)過(guò)程中,當(dāng)∠OAG′是直角時(shí)���,求α的度數(shù);
②若正方形ABCD的邊長(zhǎng)為1�����,在旋轉(zhuǎn)過(guò)程中����,求AF′長(zhǎng)的最大值和此時(shí)α的度數(shù),直接寫出結(jié)果不必說(shuō)明理由.
2
 2018中考數(shù)學(xué)專題復(fù)習(xí) 動(dòng)態(tài)旋轉(zhuǎn)問(wèn)題試題(無(wú)答案)
2018中考數(shù)學(xué)專題復(fù)習(xí) 動(dòng)態(tài)旋轉(zhuǎn)問(wèn)題試題(無(wú)答案)