《（安徽專版）2018年秋九年級數(shù)學(xué)下冊 復(fù)習(xí)自測10 圖形的變化習(xí)題 （新版）滬科版》由會員分享，可在線閱讀，更多相關(guān)《（安徽專版）2018年秋九年級數(shù)學(xué)下冊 復(fù)習(xí)自測10 圖形的變化習(xí)題 （新版）滬科版（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

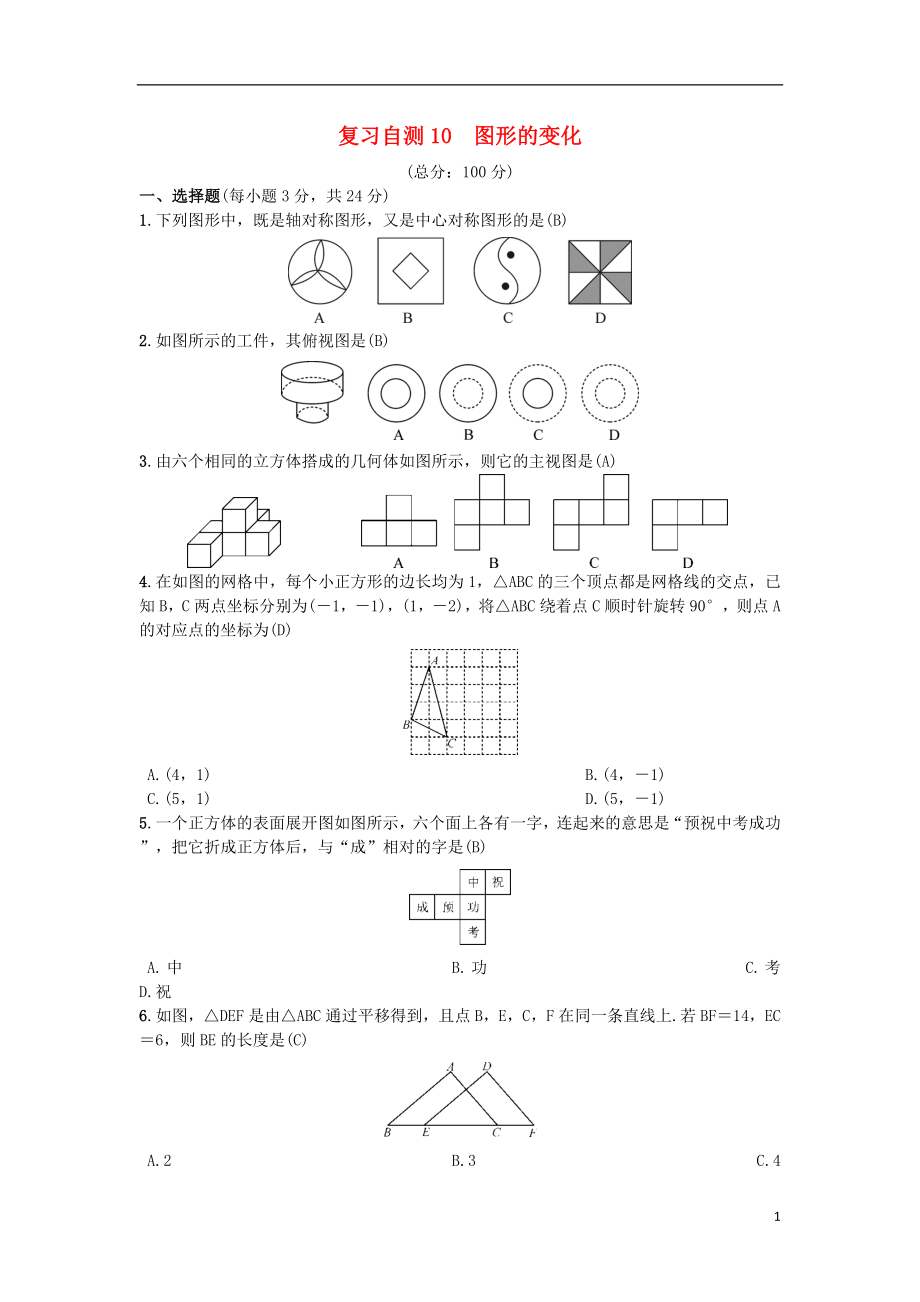
1、 復(fù)習(xí)自測10　圖形的變化 (總分：100分)　　　　　 一、選擇題(每小題3分，共24分) 1.下列圖形中，既是軸對稱圖形，又是中心對稱圖形的是(B) 2.如圖所示的工件，其俯視圖是(B) 3.由六個相同的立方體搭成的幾何體如圖所示，則它的主視圖是(A) 4.在如圖的網(wǎng)格中，每個小正方形的邊長均為1，△ABC的三個頂點都是網(wǎng)格線的交點，已知B，C兩點坐標(biāo)分別為(－1，－1)，(1，－2)，將△ABC繞著點C順時針旋轉(zhuǎn)90°，則點A的對應(yīng)點的坐標(biāo)為(D) A.(4，1)

2、 B.(4，－1) C.(5，1) D.(5，－1) 5.一個正方體的表面展開圖如圖所示，六個面上各有一字，連起來的意思是“預(yù)祝中考成功”，把它折成正方體后，與“成”相對的字是(B) A.中 B.功 C.考 D.祝 6.如圖，△DEF是由△ABC通過平移得到，且點B，E，C，F(xiàn)在同一條直線上.若BF＝14，EC＝6，則BE的長度是(C)

3、A.2 B.3 C.4 D.5 7.如圖，在等腰三角形紙片ABC中，AB＝AC，∠A＝50°，折疊該紙片，使點A落在點B處，折痕為DE，則∠CBE的度數(shù)等于(A) A.15° B.30° C.45° D.60° 8.如圖，在△ABC中，∠ACB＝90°，∠ABC＝30°，AB＝2，將△ABC繞直角頂點C逆時針旋轉(zhuǎn)60°

4、得到△A′B′C，則點B轉(zhuǎn)過的路徑長度為(B) A. B. C. D.π 二、填空題(每小題4分，共28分) 9.寫出一個三視圖完全相同的幾何體：球. 10.某幾何體的三視圖如圖所示，則組成該幾何體的小正方體的個數(shù)是5. 11.某幾何體的主視圖、左視圖和俯視圖分別如下圖所示，則該幾何體的表面積為8π. 12.如圖，把矩形ABCD沿EF折疊，使點C落在點A處，點D落在點G處.若∠CFE＝60°，且DE＝1，則BC的長3. 13.如圖

5、，在△ABC中，點D是BC上一點，連接AD，按如下步驟作圖：①以點A為圓心，以小于AD長為半徑作弧，交AD，AC于E，F(xiàn)兩點；②以點B為圓心，以AE長為半徑作弧，交BC于點P，再以點P為圓心，以EF長為半徑作弧，交前弧于點Q，連接BQ并延長交AD，AC于點M，N.若AD⊥BC，則∠ANB的度數(shù)為90°. 14.如圖，△ABC繞點A順時針旋轉(zhuǎn)45°得到△AB′C′.若∠BAC＝90°，AB＝AC＝，則圖中陰影部分的面積等于－1. 15.如圖，正△ABC的邊長為2，過點B的直線l⊥AB，且△ABC與△A′BC′關(guān)于直線l對稱，D為線段BC′上一動點，則AD＋CD的最小值是4.

6、 三、解答題(共48分) 16.(14分)如圖，在銳角△ABC中，用尺規(guī)作邊BC上的高AD，并在邊AB上找一點P，使得點P到AD兩個端點的距離相等.(保留作圖痕跡，不寫作法) 解：所作AD，點P如圖所示. 17.(16分)△ABC在平面直角坐標(biāo)系xOy中的位置如圖所示. (1)作△ABC關(guān)于點C成中心對稱的△A1B1C1; (2)將△A1B1C1向右平移4個單位長度，作出平移后的△A2B2C2，并寫出點B2的坐標(biāo). 解：(1)所作△A1B1C1如圖所示. (2)所作△A2B2C2如圖所示，此時B2(5，3). 18.(18分)將一副三角尺(在Rt△AB

7、C中，∠ACB＝90°，∠B＝60°；在Rt△DEF中，∠EDF＝90°，∠E＝45°)如圖1擺放，點D為AB的中點，DE交AC于點P，DF經(jīng)過點C. (1)求∠ADE的度數(shù)； (2)如圖2，將△DEF繞點D順時針方向旋轉(zhuǎn)角α(0°＜α＜60°)，此時的等腰直角三角尺記為△DE′F′，DE′交AC于點M，DF′交BC于點N，試判斷的值是否隨著α的變化而變化？如果不變，請求出的值；反之，請說明理由. 解：(1)∵∠ACB＝90°，點D為AB的中點， ∴CD＝AD＝BD＝AB. ∴∠ACD＝∠A＝30°. ∴∠ADC＝180°－30°×2＝120°. ∴∠ADE＝∠ADC－∠EDF＝120°－90°＝30°. (2)的值不隨著α的變化而變化，是定值.理由如下： ∵∠EDF＝90°， ∴∠PDM＋∠E′DF＝∠CDN＋∠E′DF＝90°. ∴∠PDM＝∠CDN. ∵∠B＝60°，BD＝CD， ∴△BCD是等邊三角形. ∴∠BCD＝60°. ∵∠CPD＝∠A＋∠ADE＝30°＋30°＝60°， ∴∠CPD＝∠BCD. 在△DPM和△DCN中， ∠PDM＝∠CDN，∠MPD＝∠NCD， ∴△DPM∽△DCN. 由三角形相似的性質(zhì)可知， ＝＝tan∠ACD ＝tan30° ＝. 5