《（課標通用）安徽省2019年中考數(shù)學總復習 第一篇 知識 方法 固基 第六單元 圓 考點強化練23 與圓有關的位置關系試題》由會員分享，可在線閱讀，更多相關《（課標通用）安徽省2019年中考數(shù)學總復習 第一篇 知識 方法 固基 第六單元 圓 考點強化練23 與圓有關的位置關系試題（10頁珍藏版）》請在裝配圖網上搜索。

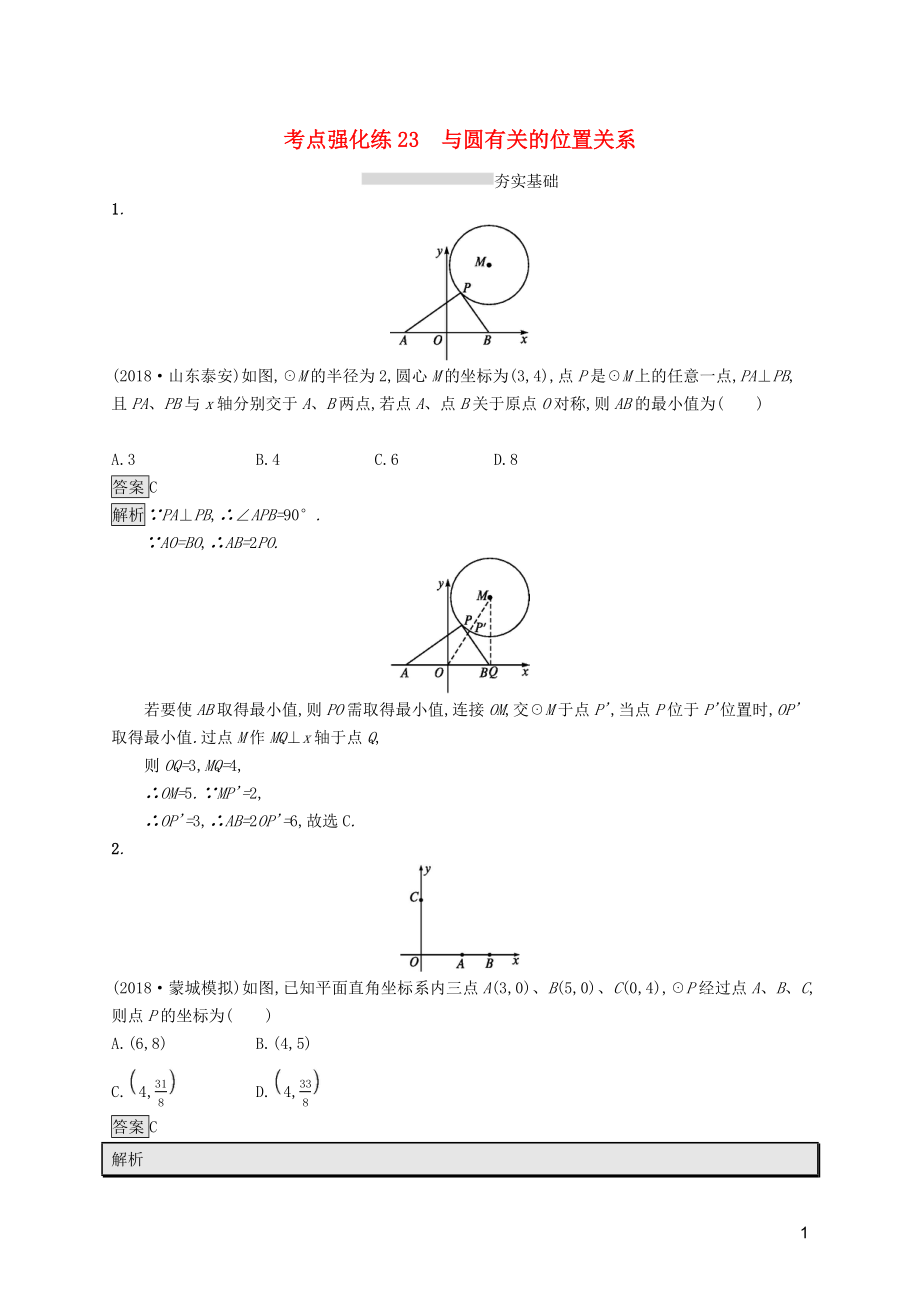
1、考點強化練23　與圓有關的位置關系 夯實基礎 1. (2018·山東泰安)如圖,☉M的半徑為2,圓心M的坐標為(3,4),點P是☉M上的任意一點,PA⊥PB,且PA、PB與x軸分別交于A、B兩點,若點A、點B關于原點O對稱,則AB的最小值為(　　) 　　　　　　　　　　　　　　 A.3 B.4 C.6 D.8 答案C 解析∵PA⊥PB,∴∠APB=90°. ∵AO=BO,∴AB=2PO. 若要使AB取得最小值,則PO需取得最小值,連接OM,交☉M于點P',當點P位于P'位置時,OP'取得最小值.過點M作MQ⊥x軸于點Q, 則OQ=3,MQ=4, ∴OM=5.∵MP

2、'=2, ∴OP'=3,∴AB=2OP'=6,故選C. 2. (2018·蒙城模擬)如圖,已知平面直角坐標系內三點A(3,0)、B(5,0)、C(0,4),☉P經過點A、B、C,則點P的坐標為(　　) A.(6,8) B.(4,5) C.4,318 D.4,338 答案C 解析 ∵☉P經過點A、B、C,∴點P在線段AB的垂直平分線上,∴點P的橫坐標為4,設點P的坐標為(4,y),作PE⊥OB于E,PF⊥OC于F,由題意得,42+(y-4)2=12+y2,解得y=318,故選C. 3.(2018·四川自貢)如圖,若△ABC內接于半徑為R的☉O,且∠A=60°,連接OB、

3、OC,則邊BC的長為(　　) A.2R B.32R C.22R D.3R 答案D 解析 延長BO交☉O于D,連接CD, 則∠BCD=90°,∠D=∠A=60°, ∴∠CBD=30°. ∵BD=2R,∴DC=R, ∴BC=3R,故選D. 4. (2018·江蘇無錫)如圖,矩形ABCD中,G是BC的中點,過A、D、G三點的☉O與邊AB、CD分別交于點E、F.給出下列說法:(1)AC與BD的交點是☉O的圓心;(2)AF與DE的交點是☉O的圓心;(3)BC與☉O相切.其中正確說法的個數(shù)是(　　) A.0 B.1 C.2 D.3 答案C 解析∵矩形ABCD中,∴∠A

4、=∠D=90°, ∴AF與DE都是☉O的直徑,AC與BD不是☉O的直徑, ∴AF與DE的交點是☉O的圓心,AC與BD的交點不是☉O的圓心, ∴(1)錯誤,(2)正確.連接AF、OG,則點O為AF的中點, ∵G是BC的中點,∴OG是梯形FABC的中位線, ∴OG∥AB.∵AB⊥BC, ∴OG⊥BC,∴BC與☉O相切. ∴(3)正確.綜上所述,正確結論有兩個. 5. (2018·浙江湖州)如圖,已知△ABC的內切圓☉O與BC邊相切于點D,連接OB,OD.若∠ABC=40°,則∠BOD的度數(shù)是　　　.? 答案70° 解析∵☉O內切于△ABC,∴OB平分∠ABC. ∵∠AB

5、C=40°,∴∠OBD=20°. ∴∠BOD=70°. 6.(2017·浙江衢州)如圖,在直角坐標系中,☉A的圓心A的坐標為(-1,0),半徑為1,點P為直線y=-34x+3上動點,過點P作☉A的切線,切點為Q,則切線長PQ的最小值是　　　　　.? 答案22 解析作切線PQ,連接PA,AQ. 有PQ=PA2-AQ2, 又AQ=1,故當AP有最小值時PQ最小. 過A作AP'⊥MN,則有AP'最小=3, 此時PQ最小=32-12=22. 7.(2017·湖南常德)如圖,已知AB是☉O的直徑,CD與☉O相切于C,BE∥CO. (1)求證:BC是∠ABE的平分線; (

6、2)若DC=8,☉O的半徑OA=6,求CE的長. (1)證明∵OC=OB,∴∠OCB=∠OBC. ∵BE∥CO,∴∠OCB=∠EBC. ∴∠OBC=∠EBC. ∴BC是∠ABE的平分線. (2)解∵CD與☉O相切于C, ∴△DCO為直角三角形. ∵DC=8,☉O的半徑OC=OA=6, ∴DO=10. ∵BE∥CO,BD和DE相交于點D, ∴DOOB=DCCE,∴CE=4.8. 8. (2018·甘肅白銀)如圖,在△ABC中,∠ABC=90°. (1)作∠ACB的平分線交AB邊于點O,再以點O為圓心,OB的長為半徑作☉O(要求:不寫作法,保留作圖痕跡). (2)判

7、斷(1)中AC與☉O的位置關系,直接寫出結果. 解(1)如圖,☉O為所求作的圓,OC為所求作的∠ACB的平分線. (2)AC為☉O的切線. 9. (2018·山東濱州)如圖,AB為☉O的直徑,點C在☉O上,AD⊥CD于點D,且AC平分∠DAB.求證: (1)直線DC是☉O的切線; (2)AC2=2AD·AO. 證明(1)連接OC,∵AC平分∠DAB, 所以∠DAC=∠OAC. 由題意可知OA=OC,∴∠OAC=∠OCA. ∴∠DAC=∠OCA,∴OC∥AD. ∵AD⊥CD,∴∠ADC=90°. ∴∠ADC=∠OCD=90°, ∴直線DC是☉O的切線. (

8、2)連接BC,因為AB是☉O的直徑, 所以∠ACB=90°, 所以∠ACB=∠ADC=90°,∠DAC=∠BAC, 所以△ADC∽△ACB, 所以ACAD=ABAC, 所以AC2=AD·AB,所以AC2=2AD·AO. 提升能力 10. (2018·江蘇泰州)如圖,△ABC中,∠ACB=90°,sin A=513,AC=12,將△ABC繞點C順時針旋轉90°得到△A'B'C,P為線段A'B'上的動點,以點P為圓心、PA'長為半徑作☉P,當☉P與△ABC的邊相切時,☉P的半徑為　　　　　　.?導學號16734133?? 答案15625或10213 解析設☉P的半徑為r,∵

9、∠ACB=90°, ∴BCAB=sinA=513,BC2+AC2=AB2. ∵AC=12,∴BC=5,AB=13. 由旋轉得∠A'CB'=∠ACB=90°,∠A'=∠A,A'C=AC=12,B'C=BC=5,A'B'=AB=13, ∴∠A'CB=180°,∴A'、C、B三點共線, ∵點P到直線BC的距離小于半徑PA', ∴☉P與直線BC始終相交,如圖1,過點P作PD⊥AC于點D,則∠B'DP=∠B'CA'=90°. 圖1 ∵∠DB'P=∠CB'A', ∴△B'DP∽△B'CA', ∴PDA'C=PB'A'B'.∴PD12=13-r13. ∴PD=12(13-r)13=

10、12-1213r. 當☉P與AC邊相切時,PD=PA', ∴12-1213r=r,∴r=15625. 如圖2,延長A'B'交AB于點E, 圖2 ∵∠A+∠B=90°,∠A'=∠A, ∴∠A'+∠B=90°,∴∠A'EB=90°, 同上得A'E=1213A'B=20413. 當☉P與AB邊相切時,A'E=2PA', ∴r=10213. 綜上所述,☉P的半徑為15625或10213. 11. (2016·江蘇無錫)如圖,△AOB中,∠O=90°,AO=8 cm,BO=6 cm,點C從A點出發(fā),在邊AO上以2 cm/s的速度向O點運動,與此同時,點D從點B出發(fā),在邊B

11、O上以1.5 cm/s的速度向O點運動,過OC的中點E作CD的垂線EF,則當點C運動了　　　　　 s時,以C點為圓心,1.5 cm為半徑的圓與直線EF相切.? 答案178 解析當以點C為圓心,1.5cm為半徑的圓與直線EF相切時,此時,CF=1.5, ∵AC=2t,BD=32t, ∴OC=8-2t,OD=6-32t, ∵點E是OC的中點,∴CE=12OC=4-t, ∵∠EFC=∠O=90°,∠FCE=∠DCO, ∴△EFC∽△DOC,∴EFOD=CFOC. ∴EF=3OD2OC=36-32t2(8-2t)=98. 由勾股定理可知CE2=CF2+EF2, ∴(4-t)2=32

12、2+982, 解得t=178或t=478, ∵0≤t≤4,∴t=178. 12. (2018·四川綿陽)如圖,AB是☉O的直徑,點D在☉O上(點D不與A,B重合).直線AD交過點B的切線于點C,過點D作☉O的切線DE交BC于點E. (1)求證:BE=CE; (2)若DE∥AB,求sin∠ACO的值. (1)證明連接OD,如圖, ∵EB,ED為☉O的切線, ∴EB=ED,OD⊥DE,AB⊥CB, ∴∠ADO+∠CDE=90°,∠A+∠ACB=90°. ∵OA=OD,∴∠A=∠ADO. ∴∠CDE=∠ACB. ∴EC=ED.∴BE=CE. (2)解作OH⊥AD于

13、H,如圖,設☉O的半徑為r, ∵DE∥AB,∴∠DOB=∠DEB=90°. ∴四邊形OBED為矩形,而OB=OD, ∴四邊形OBED為正方形, ∴DE=CE=r. 易得△AOD和△CDE都為等腰直角三角形, ∴OH=DH=22r,CD=2r. 在Rt△OCB中,OC=(2r)2+r2=5r, 在Rt△OCH中,sin∠OCH=OHOC=22r5r=1010, 即sin∠ACO的值為1010. 創(chuàng)新拓展 13. 如圖,四邊形ABCD內接于☉O,對角線AC為☉O的直徑,過點C作AC的垂線交AD的延長線于點E,點F為CE的中點,連接DB,DC,DF. (1)求∠CDE的

14、度數(shù); (2)求證:DF是☉O的切線; (3)若AC=25DE,求tan∠ABD的值. (1)解∵對角線AC為☉O的直徑, ∴∠ADC=90°,∴∠CDE=90°. (2)證明如圖,連接DO, ∵∠EDC=90°,F是EC的中點,∴DF=FC, ∴∠FDC=∠FCD, ∵OD=OC, ∴∠OCD=∠ODC, ∵∠OCF=90°, ∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°, 又∵點D在☉O上,∴DF是☉O的切線. (3)解由題意可得∠ABD=∠ACD, ∵∠E+∠DCE=90°,∠DCA+∠DCE=90°, ∴∠DCA=∠E, 又∵∠ADC=∠CDE=90°, ∴△CDE∽△ADC, ∴DCAD=DEDC,∴DC2=AD·DE, ∵AC=25DE, ∴設DE=x,則AC=25x, 則AC2-AD2=AD·DE, 即(25x)2-AD2=AD·x, 整理得AD2+AD·x-20x2=0, 解得AD=4x或-5x(負數(shù)舍去), 則DC=(25x)2-(4x)2=2x, 故tan∠ABD=tan∠ACD=ADDC=4x2x=2.?導學號16734134? 10