《江蘇省九年級數(shù)學上冊 第24講 切線的性質(zhì)定理課后練習 （新版）蘇科版》由會員分享，可在線閱讀，更多相關(guān)《江蘇省九年級數(shù)學上冊 第24講 切線的性質(zhì)定理課后練習 （新版）蘇科版（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。

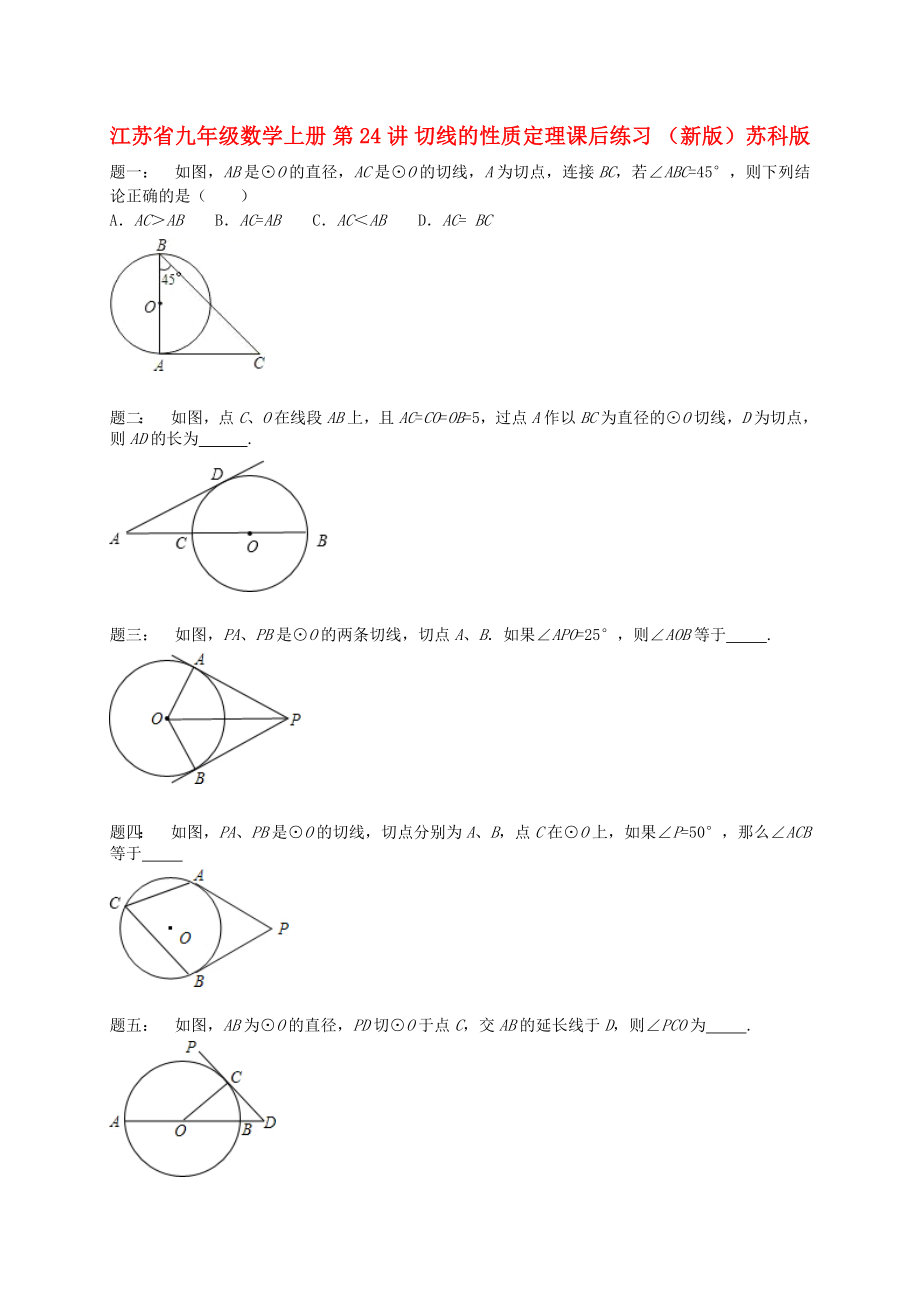
1、江蘇省九年級數(shù)學上冊 第24講 切線的性質(zhì)定理課后練習 （新版）蘇科版 題一： 如圖，AB是⊙O的直徑，AC是⊙O的切線，A為切點，連接BC，若∠ABC=45°，則下列結(jié)論正確的是（　?。? A．AC＞AB B．AC=AB C．AC＜AB D．AC= BC 題二： 如圖，點C、O在線段AB上，且AC=CO=OB=5，過點A作以BC為直徑的⊙O切線，D為切點，則AD的長為 . 題三： 如圖，PA、PB是⊙O的兩條切線，切點A、B．如果∠APO=25°，則∠AOB等于 . 題四： 如圖，PA、PB是⊙O的切線，切點分別為A、B，

2、點C在⊙O上，如果∠P=50°，那么∠ACB等于 題五： 如圖，AB為⊙O的直徑，PD切⊙O于點C，交AB的延長線于D，則∠PCO為 . 題六： 如圖，已知PD為⊙O的直徑，直線BC切⊙O于點C，BP的延長線與CD的延長線交于點A，∠A=28°，∠B=26°，則∠PDC等于 . 題七： 已知：如圖，AB是⊙O的直徑，直線l與⊙O相切于點C，AD⊥l，垂足是D． 求證：AC平分∠DAB． 題八： 如圖，在Rt△ABC中，∠ACB=90°，D是AB邊上一點，以BD為直徑的⊙O與邊AC相切于點E，連結(jié)DE并延長，與BC的延

3、長線交于點F．求證：BD=BF. 第24講 切線的性質(zhì)定理 題一： B. 詳解：∵AC是⊙O的切線，A為切點， ∴∠A=90°， ∵∠ABC=45°， ∴△ABC是等腰直角三角形， 即AB=AC， 故選B． 題二： AD=5． 詳解：∵AD是⊙O的切線，ACB是⊙O的割線， ∴AD2=AC?AB， 又AC=5，AB=AC+CO+OB=15， ∴AD2=5×15=75， ∴AD=5．（AD=-5不合題意舍去）． 題三： 130°. 詳解：∵PA是圓的切線． ∴∠OAP=90° 同理∠OBP=90° 根據(jù)四邊形內(nèi)角和定理可得：∠AOB=360°-∠O

4、AP-∠OBP-∠P=360°-90°-90°-50°=130°. 題四： 65°. 詳解：連接OA、OB； ∵PA、PB是⊙O的切線，切點分別為A、B， ∴∠OAP=∠OBP=90°， ∴∠AOB=180°-∠P=130°， ∴∠ACB=∠AOB=65°． 題五： 90°. 詳解：∵PD切⊙O于點C，交AB的延長線于D， ∴CO⊥PD， ∴∠PCO=90° 題六： 36°． 詳解：連接OC， ∵直線BC切⊙O于點C， ∴∠OCB=90， ∵∠A=28°，∠B=26°， ∴∠ACB=180°-∠B-∠A=126°，∠OCD=∠ACB-∠OCB=36°； ∵OC=OD， ∴∠PDC=∠OCD=36°． 題七： 見詳解 詳解：連接OC， ∵直線l與⊙O相切于點C， ∴OC⊥CD； 又∵AD⊥CD， ∴AD∥OC， ∴∠DAC=∠ACO； 又∵OA=OC， ∴∠ACO=∠CAO， ∴∠DAC=∠CAO， 即AC平分∠DAB． 題八： 見詳解 詳解：證明：連結(jié)OE． ∵AC切⊙O于E， ∴OE⊥AC， 又∵∠ACB=90°即OE⊥AC， ∴OE∥BC ∴∠OED=∠F． 又∵OD=OE， ∴∠OED=∠ODE， ∴∠ODE=∠F ∴BD=BF