《（浙江專用）2022高考數(shù)學(xué)二輪復(fù)習(xí) 指導(dǎo)二 透視高考解題模板示范規(guī)范拿高分 模板2 立體幾何問題學(xué)案》由會員分享，可在線閱讀，更多相關(guān)《（浙江專用）2022高考數(shù)學(xué)二輪復(fù)習(xí) 指導(dǎo)二 透視高考解題模板示范規(guī)范拿高分 模板2 立體幾何問題學(xué)案（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

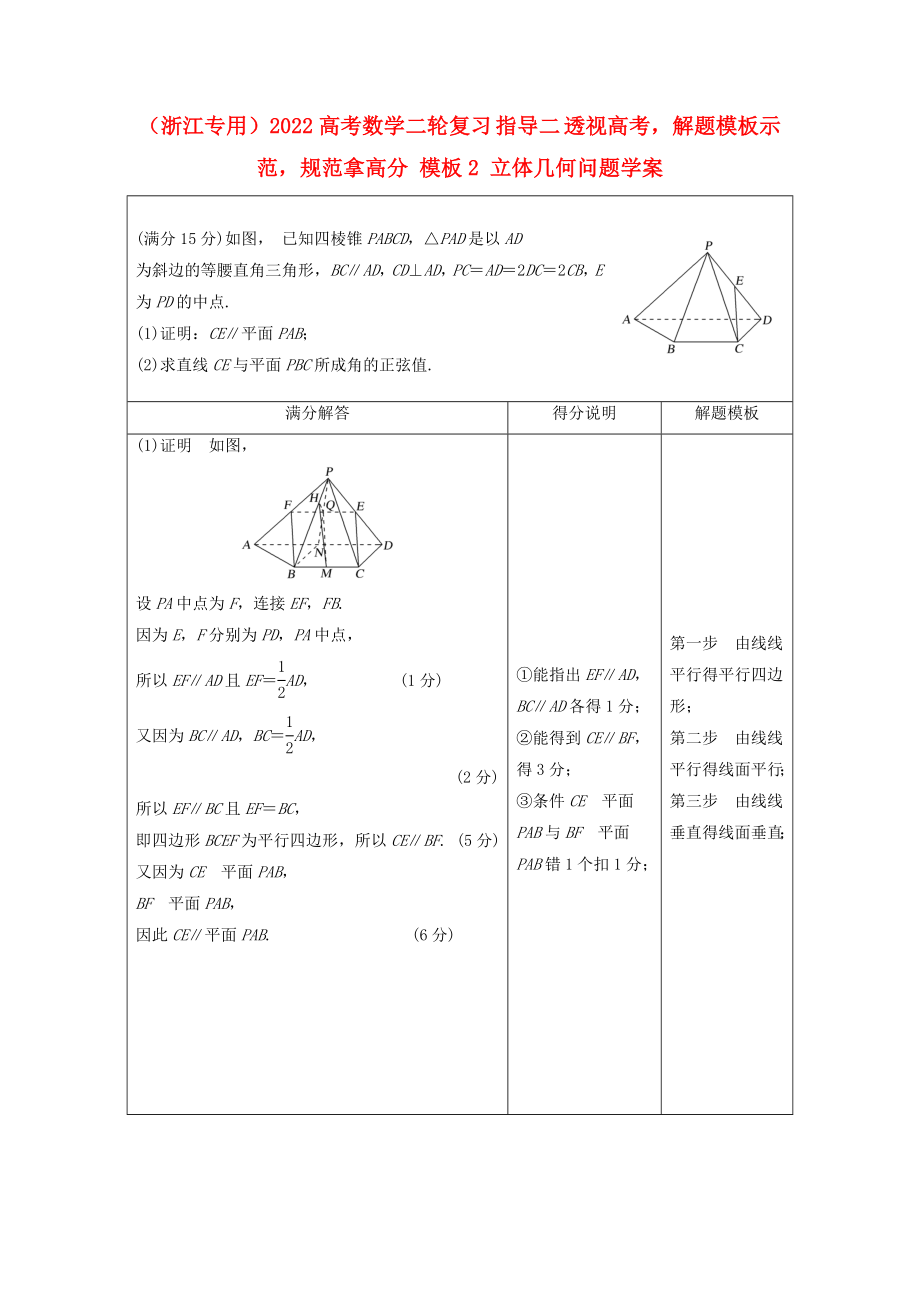
1、（浙江專用）2022高考數(shù)學(xué)二輪復(fù)習(xí) 指導(dǎo)二 透視高考，解題模板示范，規(guī)范拿高分 模板2 立體幾何問題學(xué)案 (滿分15分)如圖， 已知四棱錐PABCD，△PAD是以AD 為斜邊的等腰直角三角形，BC∥AD，CD⊥AD，PC＝AD＝2DC＝2CB，E為PD的中點. (1)證明：CE∥平面PAB； (2)求直線CE與平面PBC所成角的正弦值. 滿分解答 得分說明 解題模板 (1)證明　如圖， 設(shè)PA中點為F，連接EF，F(xiàn)B. 因為E，F(xiàn)分別為PD，PA中點， 所以EF∥AD且EF＝AD， (1分) 又因為BC∥AD，BC＝AD， (2分) 所以

2、EF∥BC且EF＝BC， 即四邊形BCEF為平行四邊形，所以CE∥BF. (5分) 又因為CE平面PAB， BF平面PAB， 因此CE∥平面PAB. (6分) ①能指出EF∥AD，BC∥AD各得1分； ②能得到CE∥BF，得3分； ③條件CE平面PAB與BF平面PAB錯1個扣1分； 第一步　由線線平行得平行四邊形； 第二步　由線線平行得線面平行； 第三步　由線線垂直得線面垂直； 第四步　得出線面角； 第五步　在三角形中計算各個邊，求值.

3、(2)解　分別取BC，AD的中點為M，N， 連接PN交EF于點Q，連接MQ. 因為E，F(xiàn)，N分別是PD，PA，AD的中點，所以Q為EF中點， 在平行四邊形BCEF中，MQ∥CE. (7分) 由△PAD為等腰直角三角形得PN⊥AD. 由DC⊥AD，BC∥AD，BC＝AD，N是AD的中點得BN⊥AD. 因為PN∩BN＝N，所以AD⊥平面PBN.(9分) 由BC∥AD得BC⊥平面PBN， 因為BC平面PBC，所以平面PBC⊥平面PBN. (11分) 過點Q作PB的垂線，垂足為H，則QH⊥平面PBC.連接MH，則MH是M

4、Q在平面PBC上的射影，所以∠QMH是直線CE與平面PBC所成的角．設(shè)CD＝1. (12分) 在△PCD中，由PC＝2，CD＝1，PD＝得CE＝， 在△PBN中，由PN＝BN＝1，PB＝得QH＝， 在Rt△MQH中，QH＝，MQ＝，所以sin∠QMH＝， 所以，直線CE與平面PBC所成角的正弦值是. (15分) ④指出MQ∥CE得1分； ⑤指出PN⊥AD，BN⊥AD，PN∩BN＝N，得2分，缺1個條件扣1分； ⑥得出BC⊥平面PBN得2分； ⑦指出∠QMH是所求角，得到1分； ⑧計算正確得3分

5、．錯誤一個量扣1分. 【訓(xùn)練2】 如圖，三棱柱ABC-A1B1C1所有的棱長均為2，A1B＝，A1B⊥AC. (1)求證：A1C1⊥B1C； (2)求直線AC和平面ABB1A1所成角的余弦值． (1)證明　法一　取AC的中點O，連接A1O，BO， ∴BO⊥AC. ∵A1B⊥AC，A1B∩BO＝B， A1B平面A1BO，BO平面A1BO， ∴AC⊥平面A1BO. 連接AB1交A1B于點M，連接OM，則B1C∥OM， 又∵OM平面A1BO，∴AC⊥OM，∴AC⊥B1C. ∵A1C1∥AC，∴A1C1⊥B1C. 法二　連接AB1，BC1，∵四邊形A1ABB1是菱形，

6、 ∴A1B⊥AB1， 又∵A1B⊥AC，AB1∩AC＝A，∴A1B⊥平面AB1C， ∴A1B⊥B1C， 又∵四邊形B1BCC1是菱形，∴BC1⊥B1C， 又∵A1B∩BC1＝B，∴B1C⊥平面A1BC1， ∴B1C⊥A1C1. (2)解　由法二知A1B⊥平面AB1C， 又∵A1B平面ABB1A1， ∴平面AB1C⊥平面ABB1A1. ∵平面AB1C∩平面ABB1A1＝AB1， ∴AC在平面ABB1A1內(nèi)的射影為AB1， ∴∠B1AC為直線AC和平面ABB1A1所成的角． ∵AB1＝2AM＝2＝， ∴在Rt△ACB1中，cos∠B1AC＝＝＝， ∴直線AC和平面ABB1A1所成角的余弦值為.