《七年級升八年級數(shù)學(xué) 暑期銜接班講義 第十六講 等邊三角形（基礎(chǔ)） 新人教版》由會員分享，可在線閱讀，更多相關(guān)《七年級升八年級數(shù)學(xué) 暑期銜接班講義 第十六講 等邊三角形（基礎(chǔ)） 新人教版（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

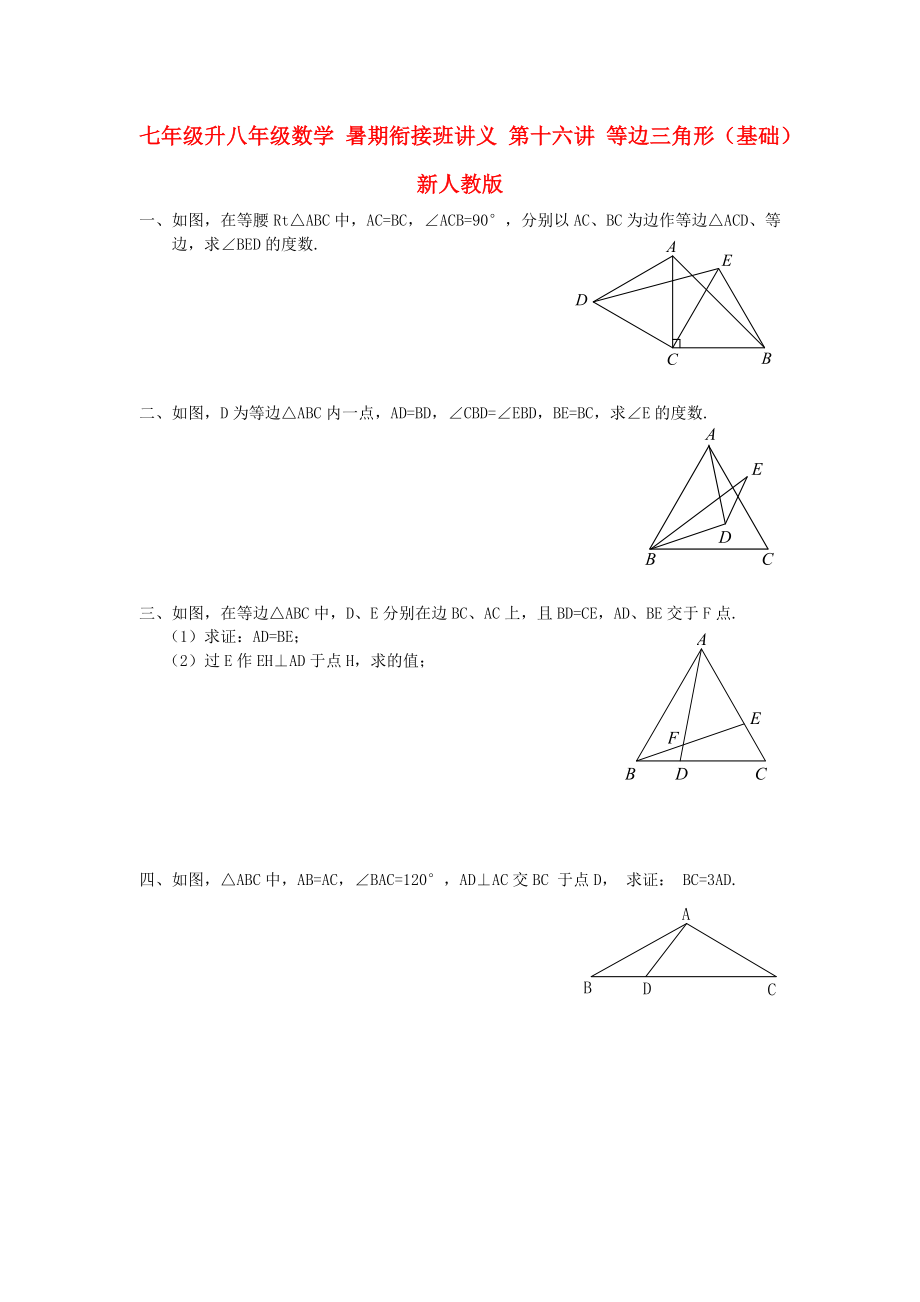
1、七年級升八年級數(shù)學(xué) 暑期銜接班講義 第十六講 等邊三角形（基礎(chǔ)） 新人教版 一、如圖，在等腰Rt△ABC中，AC=BC，∠ACB=90°，分別以AC、BC為邊作等邊△ACD、等邊，求∠BED的度數(shù). 二、如圖，D為等邊△ABC內(nèi)一點，AD=BD，∠CBD=∠EBD，BE=BC，求∠E的度數(shù). 三、如圖，在等邊△ABC中，D、E分別在邊BC、AC上，且BD=CE，AD、BE交于F點. （1）求證：AD=BE； （2）過E作EH⊥AD于點H，求的值； 四、如圖，△ABC中，AB=AC，∠BAC=120°

2、，AD⊥AC交BC于點D，求證：BC=3AD. 五、如圖，已知∠ABC=90°，△ABE是等邊三角形，點P為射線BC上任意一點（點P與點B不重合），連結(jié)AP，將線段AP繞點A逆時針旋轉(zhuǎn)60°得到線段AQ，連結(jié)QE并延長交射線BC于點F，當(dāng)點P在BC上運動時，猜想∠QFC的度數(shù)是否改變？證明你的結(jié)論. 六、如圖，等邊△ABC中，D為AC的中點，E為BC延長線上一點，DB=DE. （1）求證：AD=CE； （2）若D為AC邊上任意的一點，其它條件

3、不變，（1）中的結(jié)論是否仍然成立？證明你的結(jié)論. 第二部分【綜合運用】 七、（1）如圖，等邊△ABC，P為形外一點，∠BPC=120°. 求證：①∠APB=∠APC=60°；②PB+PC+PA. （2）如圖，等邊△ABC，P為形外一點，∠APB=60°. 求證：①∠APC=60°；②PB+PC+PA. （3）如圖，等邊△ABC，P為形外一點，AP平分∠BPC. 求證：①

4、∠APB=∠APC=60°；②PB+PC+PA. （4）如圖，在△ABC中，∠BAC=60°，P為形外一點，∠APB=∠APC=60°. 求證：①△ABC為等邊三角形；②PB+PC+PA. （5）如圖，等腰△ABC中，AB=AC，P為形外一點，∠APB=∠APC=60°. 求證：①△ABC為等邊三角形；②PB+PC+PA. （6）如圖，在△ABC中，∠ABC=60°，P為形外一點，∠APB=∠APC=60°. 求證：①△ABC為等邊三角

5、形；②PB+PC+PA. 第 16 講 作 業(yè) 一．選擇題 1．下列三角形：①有兩個角等于60°；②有一個角等于60°的等腰三角形；③三個外角（每個頂點處各取一個外角）都相等的三角形；④一腰上的中線也是這條腰上的高的等腰三角形．其中能判定該三角形是等邊三角形的有( ). (A)①②③ (B)①②④ (C)①③ (D)①②③④ 2．已知直角三角形中30°角所對的直角邊為2㎝，則斜邊的長為( ). (A)2 ㎝ (B)4

6、㎝ (C)6 ㎝ (D)8㎝ 3．Rt△ABC中，CD是斜邊AB上的高，∠B=30°，AD=2cm，則AB的長度是( ). (A)2cm (B)4cm (C)8cm (D)16cm 4. 在△ABC中，∠B=30°，∠C=45°，AD⊥BC于D，CD=2CM，則AB長為( ). (A)2cm (B)3cm (C)4cm (D)5cm 5．如圖，Rt△ABC中，∠A=30°，BD平分∠ABC

7、，若AD=8， 則CD=( ). (A)2cm (B)3cm (C)4cm (D)5cm 6．等腰三角形一腰上的高等于該三角形某一條邊的長度的一半，則其頂角等于( ). (A)30° (B)30°或150° (C)120°或150° (D)30°或120°或150° 二．填空題 7．△ABC中，∠B=∠C=15°，AB=2cm，CD⊥AB交BA的延長線于點D，則CD的長度是_______． 8．如圖C為線段AB上的一點，分別以AC、BC為邊在AB的同側(cè)作等邊△ACD和等邊△BCE，連結(jié)CD，且

8、CD⊥DE，若AB=9，則AC=_______． 9．如圖，△ABC中，AB=AC，∠A=120°，AB的垂直平分線交BC于D，若BC=12，則DE=_______． 10．如圖，等邊△ABC中，AC=9，AO=3，P為AB上的一個動點，將線段OP繞O點逆時針順序旋轉(zhuǎn)60°得到線段OQ，要使點落在BC上，則AP的長為_______． 三、解答題 11．如圖，D、E、F分別在等邊△ABC的三邊上，且AD=BE=CF，求證：△DEF為等邊三角形. 12．如圖，D、E、F分別是等邊△ABC各邊上的點，且AD=BE=CF，連接AF、BD、CE分別交于M、N、P三點，求證：△PMN為等邊三角形. 13．如圖，E是等邊△ABC中AC邊上的點，∠1=∠2，BE=CD，求證：△ADE為等邊三角形. 14. 如圖，△ABC中，AB=AC，∠BAC=120°，AD⊥AC交BC于點D，求證：BC=3AD.