《高中數(shù)學 第三章 導數(shù)及其應用 3.1 導數(shù) 3.1.2 瞬時速度與導數(shù) 3.1.3 導數(shù)的幾何意義教案 新人教B版選修1-1（通用）》由會員分享，可在線閱讀，更多相關《高中數(shù)學 第三章 導數(shù)及其應用 3.1 導數(shù) 3.1.2 瞬時速度與導數(shù) 3.1.3 導數(shù)的幾何意義教案 新人教B版選修1-1（通用）（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。

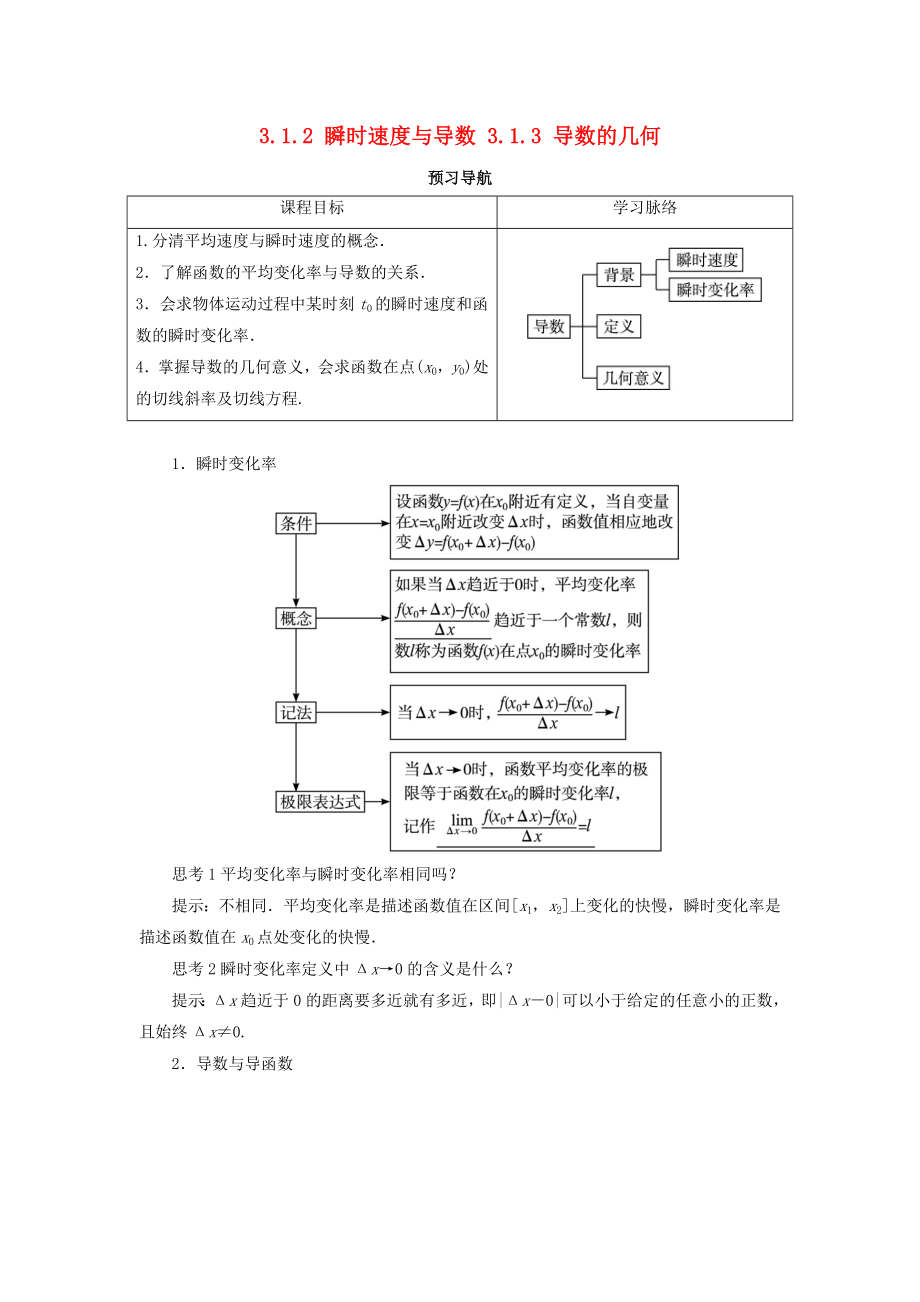
1、3.1.2 瞬時速度與導數(shù) 3.1.3 導數(shù)的幾何 預習導航 課程目標 學習脈絡 1.分清平均速度與瞬時速度的概念． 2．了解函數(shù)的平均變化率與導數(shù)的關系． 3．會求物體運動過程中某時刻t0的瞬時速度和函數(shù)的瞬時變化率． 4．掌握導數(shù)的幾何意義，會求函數(shù)在點(x0，y0)處的切線斜率及切線方程. 1．瞬時變化率 思考1平均變化率與瞬時變化率相同嗎？ 提示：不相同．平均變化率是描述函數(shù)值在區(qū)間[x1，x2]上變化的快慢，瞬時變化率是描述函數(shù)值在x0點處變化的快慢． 思考2瞬時變化率定義中Δx→0的含義是什么？ 提示：Δx趨近于0的距離要多近就有多近，即|Δx－

2、0|可以小于給定的任意小的正數(shù)，且始終Δx≠0. 2．導數(shù)與導函數(shù) 思考3函數(shù)在某點處的導數(shù)與函數(shù)在該點的瞬時變化率相同嗎？ 提示：相同． 思考4函數(shù)f(x)在定義域內(nèi)的任一點都存在導數(shù)嗎？ 提示：不一定．存在導數(shù)的點x0首先在區(qū)間內(nèi)部，不能是區(qū)間的端點，其次是當Δx→0時，趨近于一個常數(shù)，否則就不存在導數(shù)． 特別提醒(1)函數(shù)在一點處的導數(shù)f′(x0)是一個常數(shù)，不是變量． (2)函數(shù)的導數(shù)是針對某一區(qū)間內(nèi)任意點x而言的．函數(shù)f(x)在區(qū)間(a，b)內(nèi)每一點都可導，是指對于區(qū)間(a，b)內(nèi)每一個確定的值x0，都對應著一個確定的導數(shù)f′(x0)．根據(jù)函數(shù)的定義，在開區(qū)間(a，b)內(nèi)就構成了一個新的函數(shù)，就是函數(shù)f(x)的導函數(shù)f′(x)． (3)函數(shù)y＝f(x)在點x0處的導數(shù)f′(x0)就是導函數(shù)f′(x)在點x＝x0處的函數(shù)值，即f′(x0)＝f′(x)|x＝x0. 3．導數(shù)的幾何意義 思考5曲線的切線與曲線只有一個公共點嗎？ 提示：不一定．切線只是一個局部概念，是該點處的割線的極限情況，在其他位置可能還有一個或多個公共點．