《金識(shí)源專(zhuān)版高中數(shù)學(xué) 2.3.3 直線(xiàn)與平面垂直的性質(zhì)素材 新人教A版必修2》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《金識(shí)源專(zhuān)版高中數(shù)學(xué) 2.3.3 直線(xiàn)與平面垂直的性質(zhì)素材 新人教A版必修2（6頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

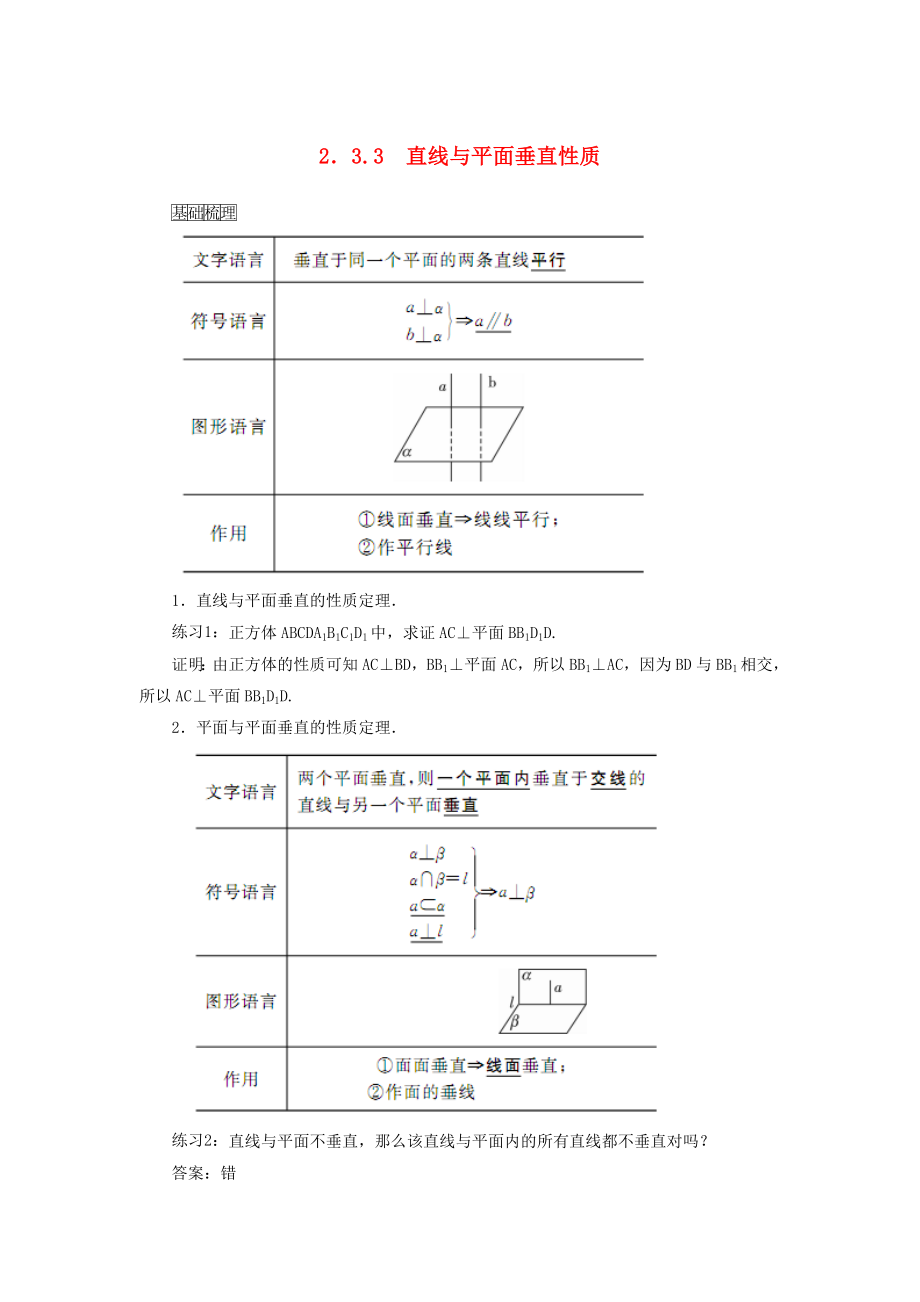
1、2．3.3　直線(xiàn)與平面垂直性質(zhì) 1．直線(xiàn)與平面垂直的性質(zhì)定理． 正方體ABCDA1B1C1D1中，求證AC⊥平面BB1D1D. 證明：由正方體的性質(zhì)可知AC⊥BD，BB1⊥平面AC，所以BB1⊥AC，因?yàn)锽D與BB1相交，所以AC⊥平面BB1D1D. 2．平面與平面垂直的性質(zhì)定理． 直線(xiàn)與平面不垂直，那么該直線(xiàn)與平面內(nèi)的所有直線(xiàn)都不垂直對(duì)嗎？ 答案：錯(cuò) ?思考應(yīng)用 1．垂直于同一平面的兩平面平行嗎？ 解析：不一定．可能平行，也可能相交，如相鄰的墻面與地面都垂直，但兩墻面相交． 2．兩個(gè)平面垂直，其中一個(gè)平面內(nèi)的任一條直線(xiàn)與另一個(gè)平面一定垂直嗎？ 解析：不一

2、定．只有垂直于兩平面的交線(xiàn)才能垂直于另一個(gè)平面． 　　　　　　　　　　　　　　　 1．若直線(xiàn)a⊥直線(xiàn)b，且a⊥平面α，則有(D) A．b∥α　 B．b?α　 C．b⊥α　 D．b∥α或b?α 2．兩個(gè)平面互相垂直，一個(gè)平面內(nèi)的一條直線(xiàn)與另一個(gè)平面(D) A．垂直 B．平行 C．平行或相交 D．平行或相交或直線(xiàn)在另一個(gè)平面內(nèi) 3．若直線(xiàn)l⊥平面α，直線(xiàn)m?平面β，有下列四個(gè)命題： ①α∥β?l⊥m　②α⊥β?l∥m?、踠∥m?α⊥β ④l⊥m?α∥β 其中正確的命題的序號(hào)是(D) A．①② B．③④ C．②④ D．①③ 4．如圖，?ADEF的邊AF垂直于

3、平面ABCD，AF＝2，CD＝3，則CE＝． 解析：∵AF∥ED，AF⊥平面ABCD， ∴ED⊥平面ABCD.∴ED⊥DC. 在Rt△EDC中，ED＝2，CD＝3， ∴CE＝＝. 1．△ABC所在的平面為α，直線(xiàn)l⊥AB，l⊥AC，直線(xiàn)m⊥BC，m⊥AC，則直線(xiàn)l，m的位置關(guān)系是(C) A．相交 B．異面 C．平行 D．不確定 解析：?l⊥a，?m⊥a. 由線(xiàn)面垂直的性質(zhì)定理得m∥l，故選C. 2．如圖，PA⊥平面ABCD，且四邊形ABCD為矩形，下列結(jié)論中不正確的是(C) A．PB⊥BC　　　　B．PD⊥C

4、D C．PO⊥BD　　　　D．PA⊥BD 3．已知平面α、β和直線(xiàn)m、l，則下列命題中正確的是(D) A．若α⊥β，α∩β＝m，l⊥m，則l⊥β B．若α∩β＝m，l?α，l⊥m，則l⊥β C．若α⊥β，l?α，則l⊥β D．若α⊥β，α∩β＝m，l?α，l⊥m，則l⊥β 解析：選項(xiàng)A缺少了條件：l?α；選項(xiàng)B缺少了條件：α⊥β；選項(xiàng)C缺少條件α∩β＝m，l⊥m；選項(xiàng)D具備了面面垂直的性質(zhì)定理的全部條件． 4．平面α⊥平面β，直線(xiàn)a∥α，則a與β的位置關(guān)系為_(kāi)_________． 答案：a∥β或a?β或a與β相交 5．圓O的半徑為4，PO垂直圓O所在的平面，且PO＝3，那么

5、點(diǎn)P到圓上各點(diǎn)的距離是________． 答案：5 6．如圖所示，平面α⊥平面β，在α與β的交線(xiàn)l上取線(xiàn)段AB＝4 cm，AC，BD分別在平面α和平面β內(nèi)，AC⊥l，BD⊥l，AC＝3 cm，BD＝12 cm，求線(xiàn)段CD的長(zhǎng)． 解析：連接AD，在Rt△ABD中，BD＝12，AB＝4， ∴AD＝＝4(cm)． ∵AC⊥l，AC?面α，α⊥β，α∩β＝l， ∴AC⊥Β. 又AD?β，∴CA⊥AD. 在Rt△ADC中，AC＝3，AD＝4， ∴CD＝＝＝13(cm)． 7．已知，△ABC所在平面外一點(diǎn)V，VB⊥平面ABC，平面VAB⊥平面VAC.求證：AC⊥BA.

6、 證明：過(guò)B作BD⊥VA于D， ∵平面VAB⊥平面VAC， ∴BD⊥平面VAC， ∴BD⊥AC， 又∵VB⊥平面ABC， ∴VB⊥AC， 又∵BD∩VB＝B， ∴AC⊥平面VBA， ∴AC⊥BA. 8．如下圖(左)所示，在邊長(zhǎng)為1的等邊三角形ABC中，D，E分別是AB，AC邊上的點(diǎn)，AD＝AE，F(xiàn)是BC的中點(diǎn)，AF與DE交于點(diǎn)G，將△ABF沿AF折起，得到如下圖(右)所示的三棱錐ABCF，其中BC＝. (1)證明：DE∥平面BCF； (2)證明：CF⊥平面ABF. (3)當(dāng)AD＝時(shí)，求三棱錐FDEG的體積VF－DEG. 解析：(

7、1)在等邊三角形ABC中，AD＝AE， ∴＝，在折疊后的三棱錐ABCF中也成立， ∴DE∥BC. 又∵DE?平面BCF，BC?平面BCF， ∴DE∥平面BCF. (2)在等邊三角形ABC中，F(xiàn)是BC的中點(diǎn)，所以AF⊥BC，即AF⊥CF，① 且BF＝CF＝. ∵在三棱錐ABCF中，BC＝， ∴BC2＝BF2＋CF2. ∴CF⊥BF.② ∵BF∩AF＝F，∴CF⊥平面ABF. (3)由(1)可知，GE∥CF，結(jié)合(2)可得GE⊥平面DFG. ∴VFDEG＝VEDFG＝××DG×FG×GE＝××××＝. 1．(1)直線(xiàn)與平面垂直的性質(zhì)：①定義：若a⊥α，b?α，則a⊥b；②性質(zhì)定理：a⊥α，b⊥α，則a∥b；③a⊥α，a⊥β，則α∥β. (2)平面與平面垂直的性質(zhì)：①性質(zhì)定理：α⊥β，α∩β＝l，m?β，m⊥l，則m⊥α.②如果兩個(gè)平面垂直，那么經(jīng)過(guò)第一個(gè)平面內(nèi)的一點(diǎn)垂直于第二個(gè)平面的直線(xiàn)在第一個(gè)平面內(nèi)． 2．直線(xiàn)與平面垂直的性質(zhì)、面面垂直的性質(zhì)，結(jié)合其判定定理，其核心思想是轉(zhuǎn)化思想，即實(shí)現(xiàn)了線(xiàn)面垂直、線(xiàn)線(xiàn)垂直、面面垂直的相互轉(zhuǎn)化，而且溝通了平行和垂直的內(nèi)在聯(lián)系，實(shí)現(xiàn)了平行和垂直的相互轉(zhuǎn)化．