《2019高考數(shù)學三輪沖刺 大題提分 大題精做8 立體幾何：動點與設(shè)未知量 理》由會員分享，可在線閱讀，更多相關(guān)《2019高考數(shù)學三輪沖刺 大題提分 大題精做8 立體幾何：動點與設(shè)未知量 理（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

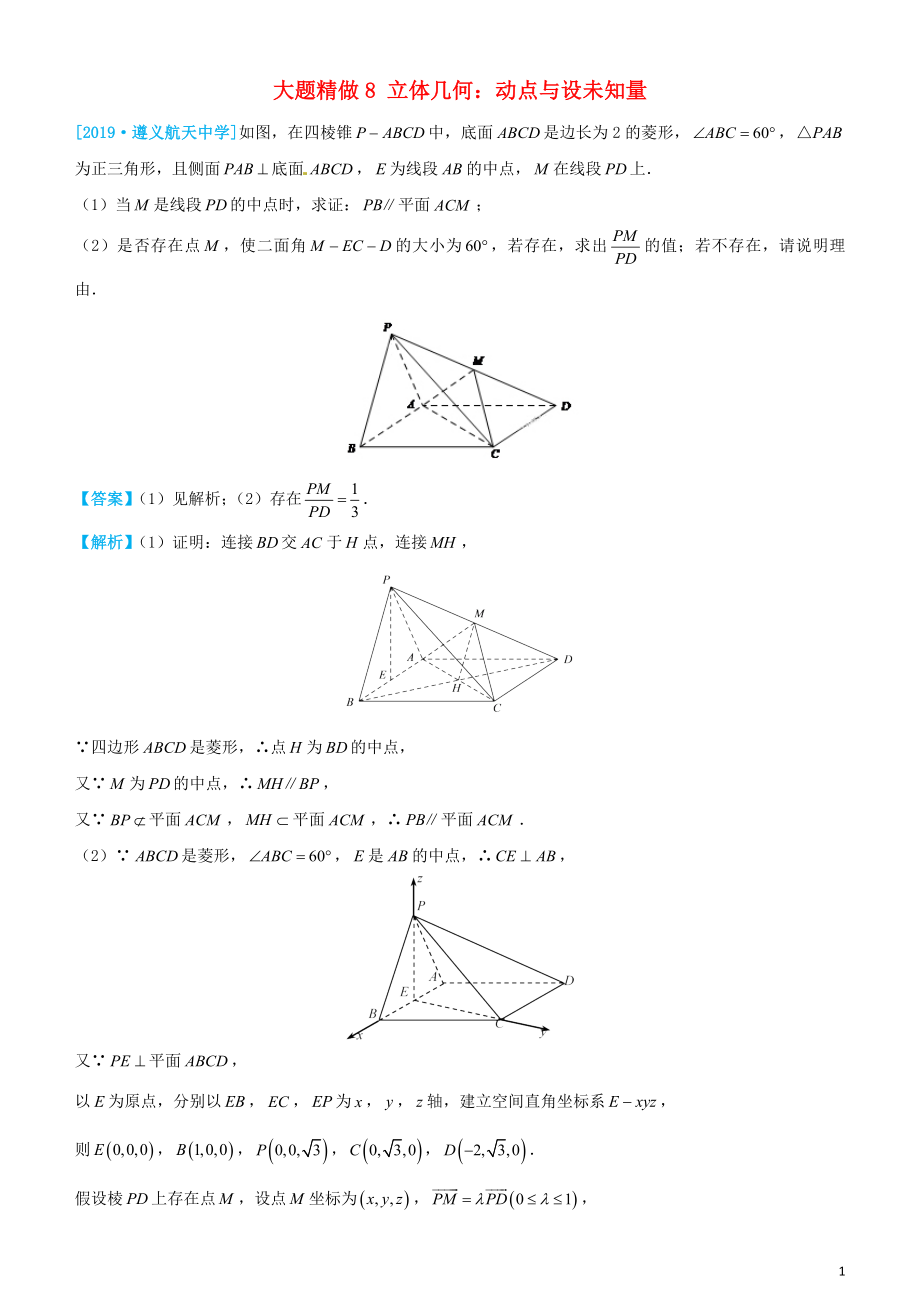
1、大題精做8 立體幾何：動點與設(shè)未知量 [2019·遵義航天中學]如圖，在四棱錐中，底面是邊長為2的菱形，，為正三角形，且側(cè)面底面，為線段的中點，在線段上． （1）當是線段的中點時，求證：平面； （2）是否存在點，使二面角的大小為，若存在，求出的值；若不存在，請說明理由． 【答案】（1）見解析；（2）存在． 【解析】（1）證明：連接交于點，連接， ∵四邊形是菱形，∴點為的中點， 又∵為的中點，∴， 又∵平面，平面，∴平面． （2）∵是菱形，，是的中點，∴， 又∵平面， 以為原點，分別以，，為，，軸，建立空間直角坐標系， 則，，，，． 假設(shè)棱上存在點，設(shè)點坐標

2、為，， 則，∴， ∴，， 設(shè)平面的法向量為， 則，解得． 令，則，得． ∵平面，∴平面的法向量， ∴， ∵二面角的大小為， ∴，即，解得，或（舍去） ∴在棱上存在點，當時，二面角的大小為． 1．[2019·躍華中學]如圖所示，正四棱椎中，底面的邊長為2，側(cè)棱長為． （1）若點為上的點，且平面，試確定點的位置； （2）在（1）的條件下，點為線段上的一點且，若平面和平面所成的銳二面角的余弦值為，求實數(shù)的值． 2．[2019·湖北聯(lián)考]如圖，在四棱錐中，，，，且 ，．

3、 （1）證明：平面； （2）在線段上，是否存在一點，使得二面角的大小為？如果存在，求的值；如果不存在，請說明理由． 3．[2019·西城44中]如圖，在四棱錐中，底面是平行四邊形，，側(cè)面底面，，，，分別為，的中點，點在線段上． （1）求證：平面； （2）若為的中點，求證：平面； （3）如果直線與平面所成的角和直線與平面所在的角相等，求的值． 1．【答案】（1）為中

4、點；（2）． 【解析】（1）設(shè)交于點，連結(jié)， ∵平面，平面平面，∴， 又為的中點，∴在中，為中點． （2）連結(jié)，由題意得平面，且， ∴以為原點，、、所成直線為，，軸，建立空間直角坐標系， ， ∴，，，，， 則，，，， 設(shè)平面的法向量， 則，令，得平面的一個法向量， 設(shè)平面的法向量， 由，得，， ∴，令，得， ∵平面和平面所成的銳二面角的余弦值為， ∴，解得． 2．【答案】（1）見證明；（2）見解析． 【解析】（1）∵在底面中，，，且， ∴，，∴， 又∵，，平面，平面，∴平面， 又∵平面，∴， ∵，，∴， 又∵，，平面，平面， ∴平面． （2）

5、方法一：在線段上取點，使，則， 又由（1）得平面，∴平面， 又∵平面，∴，作于， 又∵，平面，平面，∴平面， 又∵平面，∴， 又∵，∴是二面角的一個平面角， 設(shè)，則，， 這樣，二面角的大小為， 即， 即，∴滿足要求的點存在，且． 方法二：取的中點，則、、三條直線兩兩垂直 ∴可以分別以直線、、為、、軸建立空間直角坐標系， 且由（1）知是平面的一個法向量， 設(shè)，則，， ∴，， 設(shè)是平面的一個法向量，則， ∴， 令，則，它背向二面角， 又∵平面的法向量，它指向二面角，這樣，二面角的大小為， 即， 即，∴滿足要求的點存在，且． 3．【答案】（1）證明見

6、解析；（2）證明見解析；（3）． 【解析】（1）證明：在平行四邊形中， ∵，，，∴， ∵，分別為，的中點，∴，∴， ∵側(cè)面底面，且，∴底面，∴， 又∵，平面，平面，∴平面． （2）證明：∵為的中點，為的中點，∴， 又∵平面，平面，∴平面， 同理，得平面， 又∵，平面，平面，∴平面平面， 又∵平面，∴平面． （3）解：∵底面，，∴，，兩兩垂直， 故以，，分別為軸，軸和軸建立如圖空間直角坐標系， 則，，，，，， ∴，，， 設(shè)，則， ∴，， 易得平面的法向量， 設(shè)平面的法向量為，則， 即，令，得， ∴直線與平面所成的角和此直線與平面所成的角相等， ∴，即， ∴，解得或（舍去）， 故． 9