《吉林省伊通縣實驗中學(xué)八年級數(shù)學(xué)下冊 第十五章 整式練習(xí) 知識梳理 新人教版》由會員分享，可在線閱讀，更多相關(guān)《吉林省伊通縣實驗中學(xué)八年級數(shù)學(xué)下冊 第十五章 整式練習(xí) 知識梳理 新人教版（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

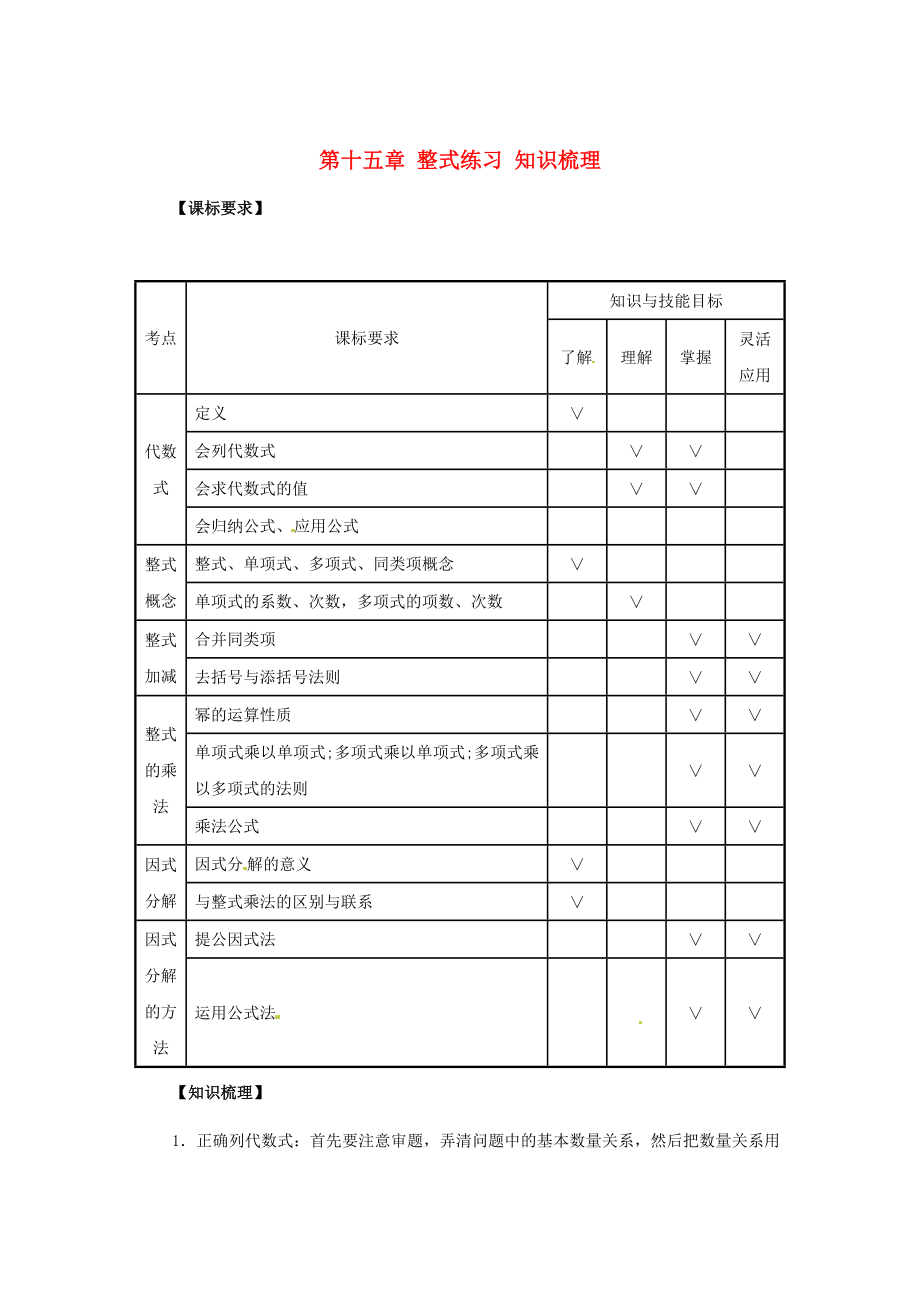
1、 第十五章 整式練習(xí) 知識梳理 　　【課標(biāo)要求】 考點 課標(biāo)要求 知識與技能目標(biāo) 了解 理解 掌握 靈活應(yīng)用 代數(shù)式 定義 ∨ 會列代數(shù)式 ∨ ∨ 會求代數(shù)式的值 ∨ ∨ 會歸納公式、應(yīng)用公式 整式概念 整式、單項式、多項式、同類項概念 ∨ 單項式的系數(shù)、次數(shù)，多項式的項數(shù)、次數(shù) ∨ 整式加減 合并同類項 ∨ ∨ 去括號與添括號法則 ∨ ∨ 整式的乘法 冪的運算性質(zhì) ∨ ∨ 單項式

2、乘以單項式;多項式乘以單項式;多項式乘以多項式的法則 ∨ ∨ 乘法公式 ∨ ∨ 因式分解 因式分解的意義 ∨ 與整式乘法的區(qū)別與聯(lián)系 ∨ 因式分解的方法 提公因式法 ∨ ∨ 運用公式法 ∨ ∨ 　　【知識梳理】 　　1．正確列代數(shù)式：首先要注意審題，弄清問題中的基本數(shù)量關(guān)系，然后把數(shù)量關(guān)系用代數(shù)式表示出來，再就是要把代數(shù)式和等式區(qū)分開，書寫代數(shù)式要注意格式。 　　2．迅速求代數(shù)式的值：求代數(shù)式的值通常要先化簡再求值比較簡便，當(dāng)所代的數(shù)是負(fù)數(shù)時，要特別注意符號。 　　3．

3、公式的探求與應(yīng)用：探求公式時要先觀察其中的規(guī)律，通過嘗試，歸納出公式，再加以驗證，這幾個環(huán)節(jié)都是必不可少的，再就是靈活運用公式解決實際問題。 　　4．正確理解整式的概念：整式的系數(shù)、次數(shù)、項、同類項等概念必須清楚，是今后學(xué)習(xí)方程、整式乘除、分式和二次函數(shù)的基礎(chǔ)。 5．熟練掌握合并同類項、去（添）括號法則：要處理好合并同類項及去（添）括號中各項符號處理，式的運算是數(shù)的運算的深化，加強(qiáng)式與數(shù)的運算對比與分析，體會其中滲透的轉(zhuǎn)化思想。 6．能熟練地運用冪的運算性質(zhì)進(jìn)行計算：冪的運算是整式的乘法的基礎(chǔ)，也是考試的重點內(nèi)容，要求熟練掌握。運算中注意“符號”問題和區(qū)分各種運算時指數(shù)的不同運算。 7

4、．能熟練運用整式的乘法法則進(jìn)行計算：整式運算常以混合運算出現(xiàn)，其中單項式乘法是關(guān)鍵，其他乘除都要轉(zhuǎn)化為單項式乘法。 8．能靈活運用乘法公式進(jìn)行計算：乘法公式的運用是重點也是難點，計算時，要注意觀察每個因式的結(jié)構(gòu)特點，經(jīng)過適當(dāng)調(diào)整后，表面看來不能運用乘法公式的式子就可以運用乘法公式，從而使計算大大簡化。 9．區(qū)分因式分解與整式的乘法：它們的關(guān)系是意義上正好相反，結(jié)果的特征是因式分解是積的形式，整式的乘法是和的形式，抓住這一特征，就不容易混淆因式分解與整式的乘法。 10．因式分解的兩種方法的靈活應(yīng)用：對于給出的多項式，首先要觀察是否有公因式，有公因式的話，首先要提公因式，然后再觀察運用公式還是分組。分解因式要分解到不能分解為止。