《2014年高考數(shù)學(xué)一輪復(fù)習(xí) 考點(diǎn)熱身訓(xùn)練 9.1基本算法語句與程序框圖》由會(huì)員分享，可在線閱讀，更多相關(guān)《2014年高考數(shù)學(xué)一輪復(fù)習(xí) 考點(diǎn)熱身訓(xùn)練 9.1基本算法語句與程序框圖（10頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

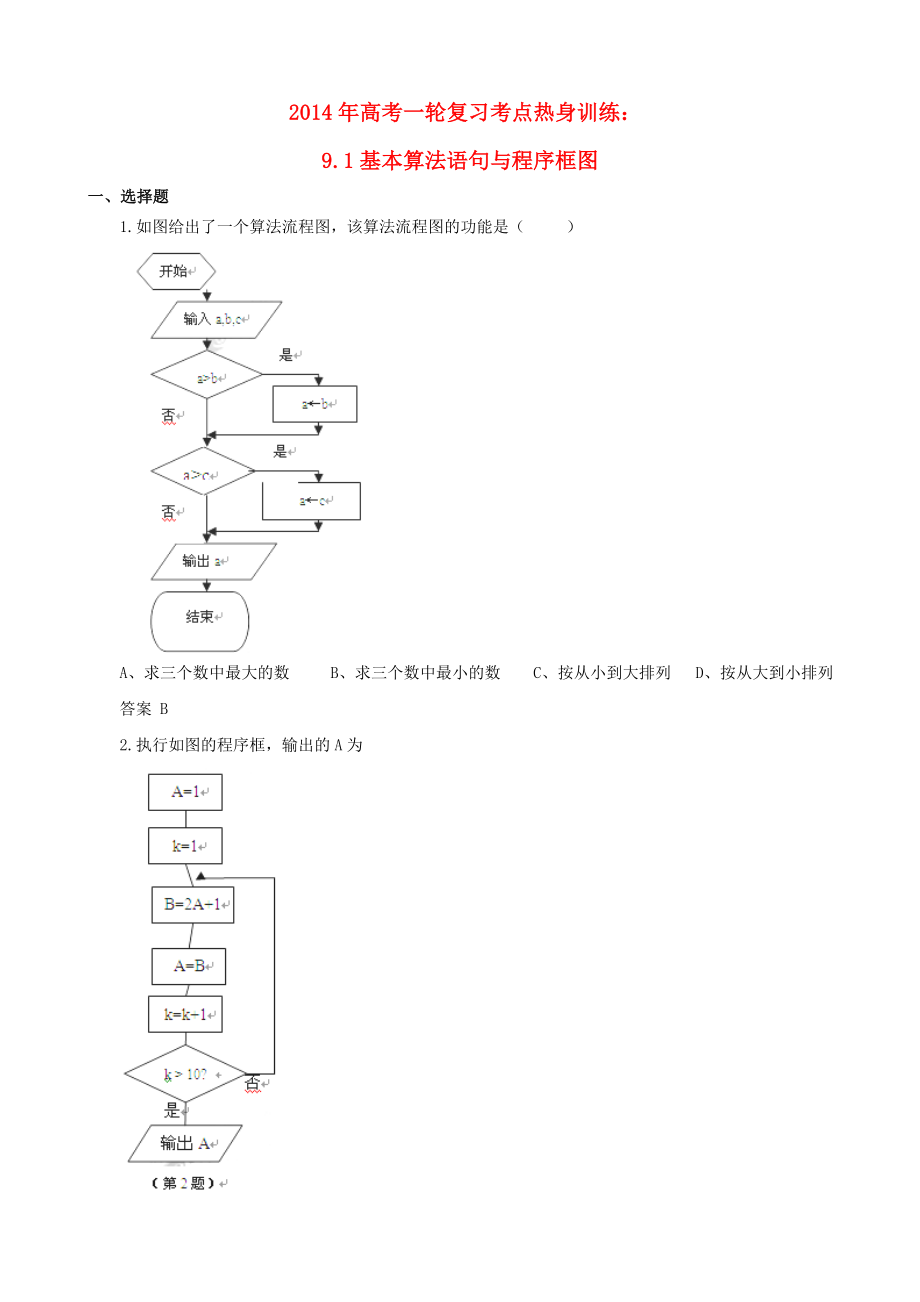
1、 2014年高考一輪復(fù)習(xí)考點(diǎn)熱身訓(xùn)練： 9.1基本算法語句與程序框圖 一、選擇題 1.如圖給出了一個(gè)算法流程圖，該算法流程圖的功能是（ ） A、求三個(gè)數(shù)中最大的數(shù) B、求三個(gè)數(shù)中最小的數(shù) C、按從小到大排列 D、按從大到小排列 答案 B 2.執(zhí)行如圖的程序框，輸出的A為 A.2047 B.2049 C.1023 D.1025 答案 A 3.若右面的程序框圖輸出的是，則①應(yīng)為 A．？ B.？ C．？ D.？ 答案 B 4、閱讀圖2的程序框圖(框圖中的賦值符號(hào)“=”也可以寫成“←”或“：

2、=”)，若輸出的S的值等于16，那么在程序框圖中的判斷框內(nèi)應(yīng)填寫的條件是 A.i>5 Bi> 6 C.i> 7 D.i> 8 答案 A 5、我市某機(jī)構(gòu)調(diào)查小學(xué)生課業(yè)負(fù)擔(dān)的情況，設(shè)平均每人每做作業(yè)時(shí)間（單位：分鐘），按時(shí)間分下列四種情況統(tǒng)計(jì)：0～30分鐘；②30～60分鐘；③60～90分鐘；④90分鐘以上，有1000名小學(xué)生參加了此項(xiàng)調(diào)查，右圖是此次調(diào)查中某一項(xiàng)的流程圖，其輸出的結(jié)果是600，則平均每天做作業(yè)時(shí)間在0～60分鐘內(nèi)的學(xué)生的頻率是 A．0.20 B．0.40 C．0.60 D．0.80 答案 B 6.如圖，程

3、庫框圖所進(jìn)行的求和運(yùn)算是 A 　　B C 　 D 答案 C 7．根據(jù)右邊程序框圖，若輸出的值是4，則輸入的實(shí)數(shù)的值為 (A) (B) (C) 或 (D) 或 答案 D 8．下邊方框中為一個(gè)求20個(gè)數(shù)的平均數(shù)的程序，則在橫線上應(yīng)填的語句為（ ） A. B. C. D. 答案：A 9.有如下算法: 第一步： 輸入大于1 的正整數(shù)n 第二步： 判斷n是否等于2，若n=2，則輸出n，結(jié)束；若n>2，則執(zhí)行第三步 第三步：依次從2到n－1

4、檢驗(yàn)?zāi)懿荒苷齨，若不能整除n,則輸出n，結(jié)束；否則執(zhí)行第四步 第四步 輸出“不滿足條件” 這個(gè)算法如果輸出n的值，那么這個(gè)n是 ( ) A．質(zhì)數(shù) B．奇數(shù) C．偶數(shù) D.一定是2 答案：A 10. 執(zhí)行右邊的程序框圖，若輸出y的值為2，則輸入的x應(yīng)該是（ ） A．或 B．或 C． 　 D．或 答案：D 11. 計(jì)算機(jī)執(zhí)行下面的程序段后，輸出的結(jié)果是（ B ） PRINT ， A．1,3 B．4,1 C．0

5、,0 D．6,0 答案：B．4,1 12.如下圖是一個(gè)算法的程序框圖，當(dāng)輸入的值為3時(shí)，輸出的結(jié)果恰好是，則空白處的關(guān)系式可以是（ ） A． B． C． D． 答案：C 二、填空題 13．如上圖所示算法程序框圖中，令，則輸出結(jié)果為______． 答案 14．對(duì)一個(gè)作直線運(yùn)動(dòng)的質(zhì)點(diǎn)的運(yùn)動(dòng)過程觀測(cè)了8次, 第次觀測(cè)得到的數(shù)據(jù)為，具體如下表所示： 1 2 3 4 5 6 7 8 40 41 43 43 44 46 47 48 在對(duì)上述統(tǒng)計(jì)數(shù)據(jù)的分析中，一部分計(jì)算見如圖所示的

6、算法流程 圖(其中是這8個(gè)數(shù)據(jù)的平均數(shù))，則輸出的的值是_ 答案 7 15．用秦九韶算法計(jì)算函數(shù)當(dāng)x＝2時(shí)的函數(shù)值為 . 答案：62 16. 執(zhí)行右邊的程序框圖，若輸出y的值為2，則輸入的x應(yīng)該是 答案：或 三、解答題 17. 根據(jù)如圖所示的程序框圖，將輸出的x、y值依次分別記為； （Ⅰ）求數(shù)列的通項(xiàng)公式； （Ⅱ）寫出y1，y2，y3，y4，由此猜想出數(shù)列{yn}的一個(gè)通項(xiàng)公式y(tǒng)n，并證明你的結(jié)論; （Ⅲ）求 解：（Ⅰ）由框圖，知數(shù)列 ……2分 ∴ ……3分 （Ⅱ）y1=2，y2=8，

7、y3=26，y4=80. 由此，猜想 ……5分 證明：由框圖，知數(shù)列{yn}中，yn+1=3yn+2 ∴ ∴數(shù)列{yn+1}是以3為首項(xiàng)，3為公比的等比數(shù)列?！?分 ∴+1=3·3n－1=3n ∴=3n－1（） ……8分 （Ⅲ）zn= =1×（3－1）+3×（32－1）+…+（2n－1）（3n－1）=1×3+3×32+…+（2n－1）·3n－[1+3+…+（2n－1）] ……9分 記Sn=1×3+3×32+…+（2n－1）·3n，① ……10分 則3Sn=1×32+3×33+…+（2n－1）×3n+1 ② ①－②，得－2Sn=3+2·32+2·33+…+2·3n－（2n－1）·3n+1 =2（3+32+…+3n）－3－（2n－1）·3n+1 =2×= ∴ ……12分 又1+3+…+（2n－1）=n2 ……13分 ∴. ……14分 18. （1）將下面的程序框圖改寫為程序語句。（2）將上面的程序語句改寫為程序框圖。 解答： 教學(xué)資源網(wǎng) 教學(xué)資源網(wǎng)