《人教版初三數(shù)學(xué)導(dǎo)學(xué)案銳角三角函數(shù)》由會(huì)員分享，可在線閱讀，更多相關(guān)《人教版初三數(shù)學(xué)導(dǎo)學(xué)案銳角三角函數(shù)（4頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

1、濠知教育學(xué)科導(dǎo)學(xué)案ggggggggggggangganggang綱 學(xué) 生 教 師 吳老師 日 期 2015/12/05 年 級(jí) 初三 學(xué) 科 數(shù)學(xué) 時(shí) 段 學(xué) 情 分 析 針對(duì)初三下冊(cè)所學(xué)的知識(shí)點(diǎn)進(jìn)行簡(jiǎn)要系統(tǒng)的復(fù)習(xí)與預(yù)習(xí)。 課 題 銳角三角函數(shù) 學(xué)習(xí)目標(biāo)與 考點(diǎn)分析 1、使學(xué)生了解方位角的命名特點(diǎn)，能準(zhǔn)確把握所指的方位角是指哪一個(gè)角 2、逐步培養(yǎng)學(xué)生分析問題、解決問題的能力；滲透數(shù)形結(jié)合的數(shù)學(xué)思想和方法． 3、鞏固用三角函數(shù)有關(guān)知識(shí)解決問題，學(xué)會(huì)解決方位角問題． 學(xué)習(xí)重點(diǎn) 難 點(diǎn) 重點(diǎn)：用三角函數(shù)有關(guān)知識(shí)解決

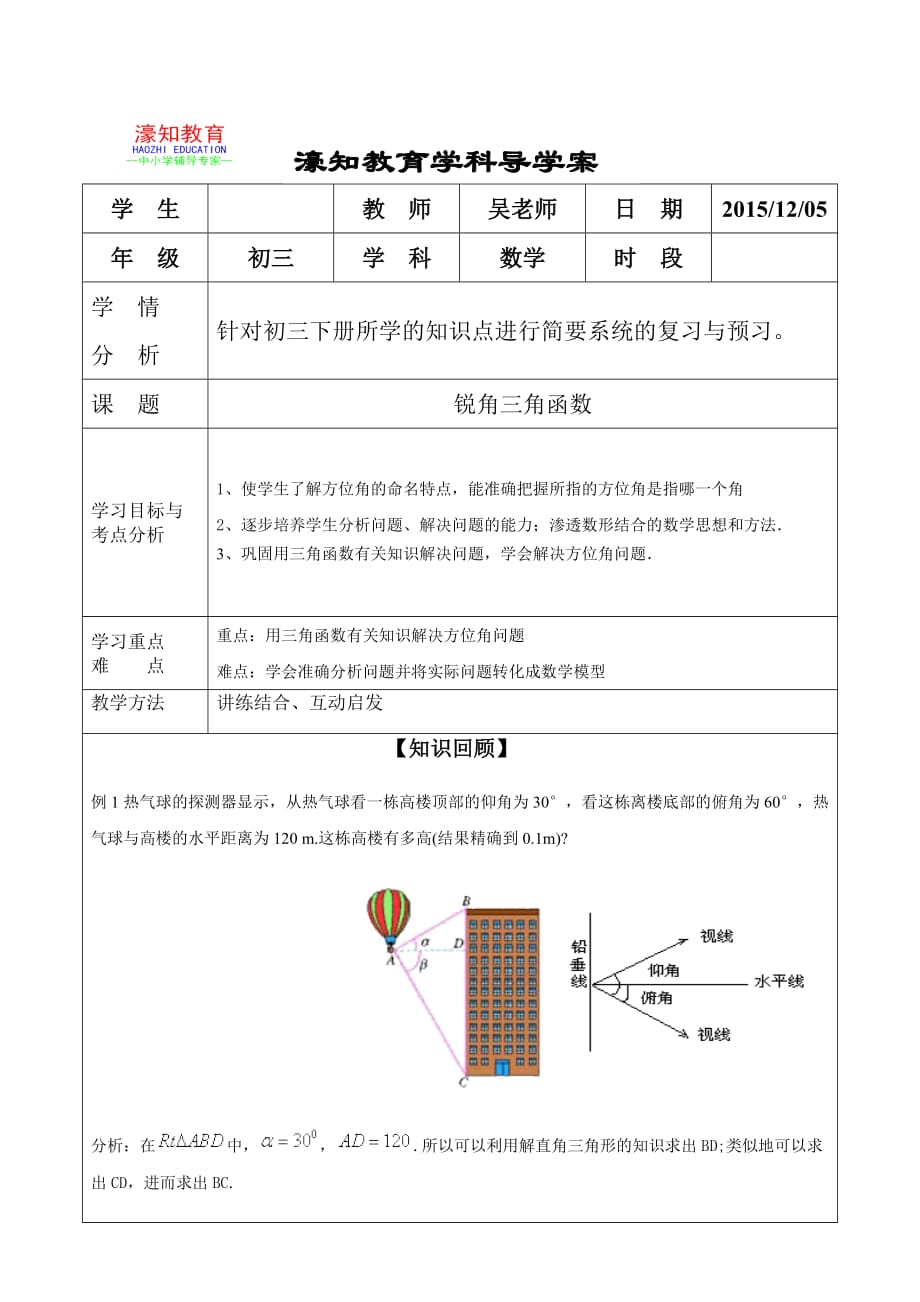
2、方位角問題 難點(diǎn)：學(xué)會(huì)準(zhǔn)確分析問題并將實(shí)際問題轉(zhuǎn)化成數(shù)學(xué)模型 教學(xué)方法 講練結(jié)合、互動(dòng)啟發(fā) 【知識(shí)回顧】 例1熱氣球的探測(cè)器顯示，從熱氣球看一棟高樓頂部的仰角為30，看這棟離樓底部的俯角為60，熱氣球與高樓的水平距離為120 m.這棟高樓有多高(結(jié)果精確到0.1m)? 分析：在中，，.所以可以利用解直角三角形的知識(shí)求出BD;類似地可以求出CD，進(jìn)而求出BC. （三）鞏固再現(xiàn) 1、為測(cè)量松樹AB的高度，一個(gè)人站在距松樹15米的E處，測(cè)得仰角∠ACD=52，已知人的高度是1.72米，求樹高(精確到0.01米)．（tan52=1.28） 2、在寬為3

3、0米的街道東西兩旁各有一樓房，從東樓底望西樓頂仰角為45，從西樓頂望東樓頂，俯角為10，求西樓高(精確到0.1米)． 3、上午10時(shí)，我軍駐某海島上的觀察所A發(fā)現(xiàn)海上有一艘敵軍艦艇正從C處向海島駛來，當(dāng)時(shí)的俯角，經(jīng)過5分鐘后，艦艇到達(dá)D處，測(cè)得俯角。已知觀察所A距水面高度為80米，我軍武器射程為100米，現(xiàn)在必須迅速計(jì)算出艦艇何時(shí)駛?cè)胛臆娀鹆ι涑讨畠?nèi)，以便及時(shí)還擊。 (1/tan5.71=10, 1/tan7.59=7.5 ) （二）教學(xué)互動(dòng) 1、上午10點(diǎn)整，一漁輪在小島O的北偏東30方向，距離等于10

4、海里的A處，正以每小時(shí)10海里的速度向南偏東60方向航行．那么漁輪到達(dá)小島O的正東方向是什么時(shí)間？(精確到1分)． 3、如圖6-32，海島A的周圍8海里內(nèi)有暗礁，魚船跟蹤魚群由西向東航行，在點(diǎn)B處測(cè)得海島A位于北偏東60，航行12海里到達(dá)點(diǎn)C處，又測(cè)得海島A位于北偏東30，如果魚船不改變航向繼續(xù)向東航行．有沒有觸礁的危險(xiǎn)？ 1． 坡度與坡角 坡面的鉛直高度h和水平寬度的比叫做坡度（或叫做坡比），一般用i表示。即ｉ＝，常寫成i=1：m的形式如

5、i=1:2.5 把坡面與水平面的夾角α叫做坡角． i＝＝tan 這一關(guān)系在實(shí)際問題中經(jīng)常用到． 練習(xí)(1)一段坡面的坡角為60，則坡度i=______；______，坡角______度． 坡面鉛直高度一定，其坡角、坡度和坡面水平寬度有什么關(guān)系？ 坡面水平寬度一定，鉛直高度與坡度有何關(guān)系 如圖，鉛直高度AB一定，水平寬度BC增加，α將變小， 坡度減小，因?yàn)?tan＝，AB不變，tan隨BC增大而減小（2）與(1)相反，水平寬度BC不變，α將隨鉛直高度增大而增大，tanα 也隨之增大，因?yàn)閠an=不變時(shí)，tan隨AB的增大而增大 例： 利用土埂修筑一條渠道，在埂中間挖去深為0.6米的一塊(圖6-35陰影部分是挖去部分)，已知渠道內(nèi)坡度為1∶1.5，渠道底面寬BC為0.5米，求： ①橫斷面(等腰梯形)ABCD的面積； ②修一條長為100米的渠道要挖去的土方數(shù)．