《（通用版）高三物理二輪復習 第2部分 考前回扣 倒計時第8天 質點運動的基本規(guī)律用書-人教版高三物理試題》由會員分享，可在線閱讀，更多相關《（通用版）高三物理二輪復習 第2部分 考前回扣 倒計時第8天 質點運動的基本規(guī)律用書-人教版高三物理試題（8頁珍藏版）》請在裝配圖網上搜索。

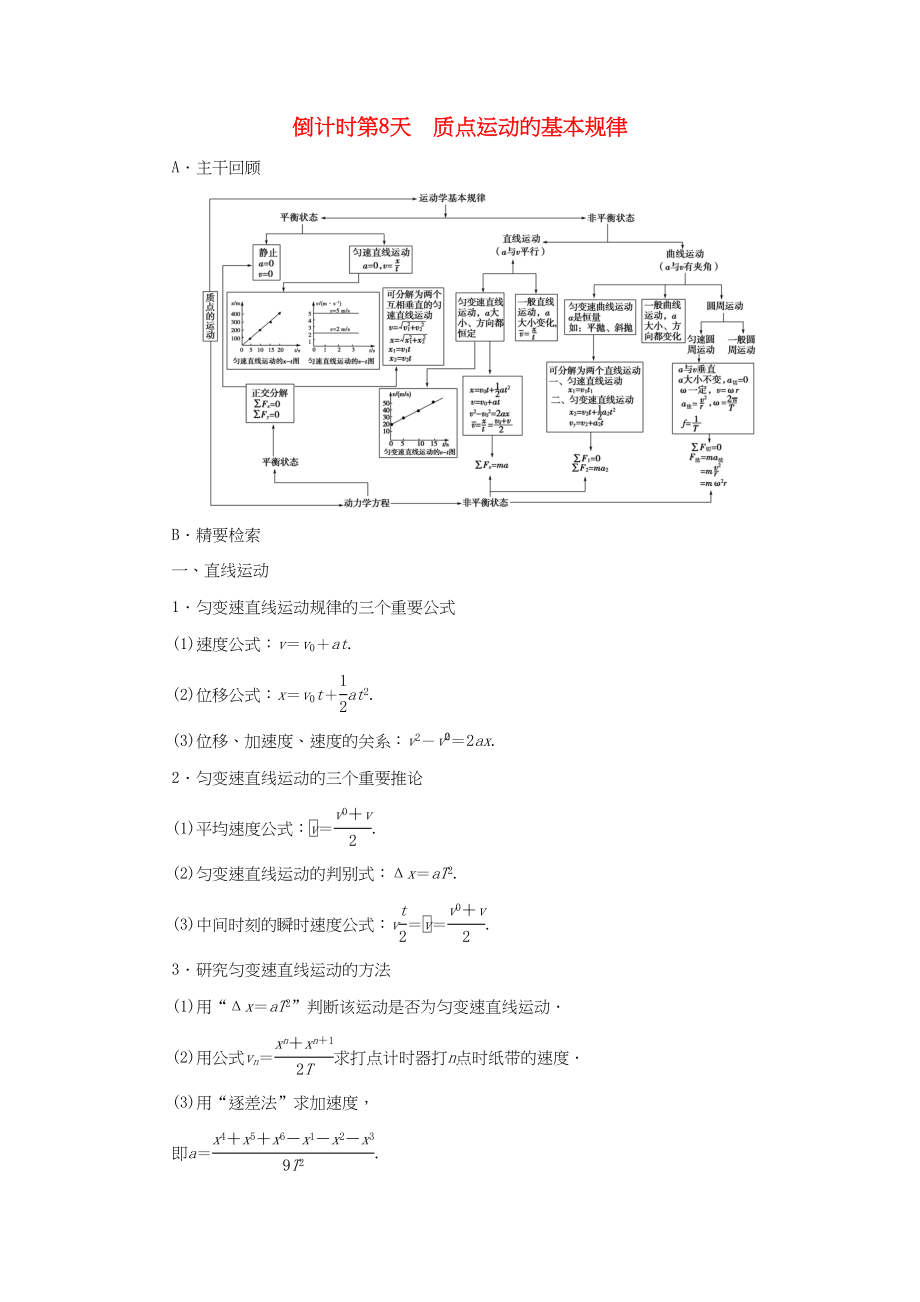
1、倒計時第8天　質點運動的基本規(guī)律 A．主干回顧 B．精要檢索 一、直線運動 1．勻變速直線運動規(guī)律的三個重要公式 (1)速度公式：v＝v0＋at. (2)位移公式：x＝v0t＋at2. (3)位移、加速度、速度的關系：v2－v＝2ax. 2．勻變速直線運動的三個重要推論 (1)平均速度公式：＝. (2)勻變速直線運動的判別式：Δx＝aT2. (3)中間時刻的瞬時速度公式：v＝＝. 3．研究勻變速直線運動的方法 (1)用“Δx＝aT2”判斷該運動是否為勻變速直線運動． (2)用公式vn＝求打點計時器打n點時紙帶的速度． (3)用“逐差法”求加速度， 即a＝.

2、 4．自由落體運動 (1)條件：①只受重力作用；②初速度為零． (2)速度公式v＝gt；位移公式x＝gt2. 二、曲線運動 1．平拋運動 (1)特點：初速度沿水平方向，只受豎直方向的重力作用，其軌跡為拋物線．平拋運動是勻變速(加速度是g)曲線運動． (2)位移關系： 水平位移x＝v0t 豎直位移y＝gt2 合位移的大小s＝，合位移的方向tan α＝. (3)速度關系： 水平速度vx＝v0，豎直速度vy＝gt. 合速度的大小v＝，合速度的方向tan β＝. (4)重要推論： 速度偏角與位移偏角的關系為tan β＝2tan α 平拋運動到任一位置A，過A點

3、作其速度方向的反向延長線交Ox軸于C點，有OC＝(如圖1所示)． 圖1 2．勻速圓周運動 (1)勻速圓周運動的規(guī)律 ①v、ω、T、f及半徑的關系：T＝，ω＝＝2πf，v＝r＝2πfr＝ωr. ②向心加速度大?。篴＝＝ω2r＝4π2f2r＝r. ③向心力大?。篎＝ma＝m＝mω2r＝mr＝4π2mf2r. (2)豎直平面內圓周運動的臨界條件 ①輕繩拉小球在豎直平面內做圓周運動(或小球在豎直圓軌道內側做圓周運動)時的臨界點是在豎直圓軌道的最高點有F＋mg＝成立；由于輕繩中拉力F≥0，要使小球能夠經過豎直圓軌道的最高點，則到達最高點時速度必須滿足v≥. ②由于經桿(或環(huán)形圓管)

4、既可提供拉力，又可提供支持力，輕桿拉小球(或環(huán)形圓管內小球)在豎直平面內做圓周運動(或小球在豎直平面內雙軌道之間做圓周運動)的條件為到達最高點時速度v≥0. 三、天體的運動 1．人造地球衛(wèi)星 (1)軌道特征：軌道平面必過地心． (2)動力學特征：萬有引力提供衛(wèi)星繞地球做圓周運動的向心力，即有G＝m＝m2r. (3)運動學特征：軌道半徑越大，周期越長，但運行速度越?。? (4)宇宙速度：發(fā)射人造地球衛(wèi)星的最小速度——第一宇宙速度v1＝＝7.9 km/s.物體脫離地球引力，不再繞地球運行所需的最小速度——第二宇宙速度；物體脫離太陽的引力所需的最小速度——第三宇宙速度． 2．地球衛(wèi)星的最

5、大運行速度和最小周期 由G＝m＝m2r，得到衛(wèi)星繞地球的運行速度v＝＝，周期T＝＝2π＝2π. 當衛(wèi)星繞地球表面運行時，軌道半徑r等于地球半徑R，運行速度最大，周期最?。? 3．地球同步衛(wèi)星四定 (1)運行周期一定，周期為24 h. (2)距地面高度一定，大約為3.6×104 km. (3)軌道平面一定，軌道平面與赤道面重合． (4)環(huán)繞方向及速度一定，環(huán)繞方向為自西向東運動，速度大小約為3.1 km/s. C．考前熱身 1．(多選)某遙控小車在平直路面上運動的v-t圖線如圖2所示．則關于小車的運動，下列說法正確的是(　　) 圖2 A．0～5 s內小車運動的路程為3 m

6、 B．小車開始以2 m/s的速度做勻速直線運動，在2～3 s內做勻加速運動，加速度的大小為2 m/s2 C．3～5 s內小車的加速度的大小為2 m/s2 D．0～5 s內小車運動的位移為11 m BC　[由圖知，小車開始以2 m/s的速度做勻速直線運動，到2 s時開始做勻加速直線運動，加速度大小為2 m/s2,3 s時速度達到4 m/s，然后突然以4 m/s的速度返回，沿反向做勻減速直線運動，加速度大小為2 m/s2，B、C正確；路程s＝2×2 m＋×1 m＋×4×2 m＝11 m，位移x＝2×2 m×＋×1 m－×4×2 m＝3 m，A、D錯誤．] 2．(多選)如圖3所示，斜面傾角

7、為θ，從斜面的P點分別以v0和2v0的速度水平拋出A、B兩個小球，不計空氣阻力，若兩小球均落在斜面上且不發(fā)生反彈，則(　　) 圖3 A．A、B兩小球的水平位移之比為1∶4 B．A、B兩小球飛行的時間之比為1∶2 C．A、B兩小球下落的高度之比為1∶2 D．A、B兩小球落到斜面上的速度大小之比為1∶4 AB　[由平拋運動規(guī)律可知，x1＝v0t1，y1＝gt，tan θ＝；x2＝2v0t2，y2＝gt，tan θ＝，聯(lián)立解得A、B兩小球飛行的時間之比為t1∶t2＝1∶2，A、B兩小球的水平位移之比為x1∶x2＝1∶4，選項A、B正確；A、B兩小球下落的高度之比為y1∶y2＝1∶4，

8、選項C錯誤；A、B兩小球落到斜面上時的速度大小分別為v1＝，v2＝＝2，即A、B兩小球落到斜面上的速度大小之比為1∶2，選項D錯誤．] 3．(多選)已知地球半徑為R，質量為M，自轉角速度為ω，引力常量為G，地球同步衛(wèi)星距地面高度為h，則(　　) A．地球表面赤道上物體隨地球自轉的線速度為ωR B．地球同步衛(wèi)星的運行速度為ωh C．地球近地衛(wèi)星做勻速圓周運動的線速度為 D．地球近地衛(wèi)星做勻速圓周運動的周期大于 AC　[地球表面赤道上物體隨地球自轉的線速度v＝ωR，選項A正確；地球同步衛(wèi)星的運行速度v′＝ω(R＋h)，選項B錯誤；由G＝m得選項C正確；只有軌道高于地球同步衛(wèi)星軌道的衛(wèi)星

9、周期才大于地球同步衛(wèi)星的周期，選項D錯誤．] 4．隨著世界航空事業(yè)的發(fā)展，深太空探測已逐漸成為各國關注的熱點．假設深太空中有一顆外星球，質量是地球質量的2倍，半徑是地球半徑的，則下列判斷正確的是(　　) A．該外星球的同步衛(wèi)星的周期一定小于地球同步衛(wèi)星的周期 B．某物體在該外星球表面所受重力是在地球表面所受重力的6倍 C．該外星球的第一宇宙速度是地球的第一宇宙速度的2倍 D．繞該外星球運行的人造衛(wèi)星和以相同軌道半徑繞地球運行的人造衛(wèi)星的速度相同 C　[因不確定外星球的同步衛(wèi)星的軌道半徑和周期，故無法與地球同步衛(wèi)星的周期比較，選項A錯誤；設地球的質量為M，半徑為R，在星體表面物體的重

10、力等于其受到的萬有引力，則＝mg，＝mg′，兩式相比可得＝，選項B錯誤；設地球的第一宇宙速度為v，外星球的第一宇宙速度為v′，則＝，＝，兩式相比可得＝，選項C正確；設人造衛(wèi)星的軌道半徑都為r，則有＝，＝，兩式相比可得＝，選項D錯誤．] 5．(多選)如圖4所示，兩個可視為質點的、相同的木塊A和B放在水平轉盤上，且木塊A、B與轉盤中心在同一條直線上，兩者用長為L的細繩連接，木塊與轉盤之間的最大靜摩擦力均為各自重力的k倍，A放在距離轉軸L處，整個裝置能繞通過轉盤中心的豎直轉軸O1O2轉動．開始時，繩恰好伸直但無彈力．現(xiàn)讓該裝置從靜止開始轉動，使角速度緩慢增大，以下說法正確的是(　　) 【導學號

11、：37162096】 圖4 A．當ω＞時，A、B相對于轉盤會滑動 B．當ω>時，繩子一定有彈力 C．ω在＜ω＜范圍內增大時，B所受的摩擦力變大 D．ω在0<ω<范圍內增大時，A所受的摩擦力一直變大 ABD　[當木塊A、B所受的靜摩擦力均達到最大值時，A、B相對轉盤將會滑動，kmg＋kmg＝mω2L＋mω2·2L，解得ω＝，選項A正確；當B所受的靜摩擦力達到最大值后，繩子開始有彈力，即kmg＝mω2·2L，解得ω＝，選項B正確；當＜ω＜時，隨角速度的增大，繩子拉力不斷增大，B所受的靜摩擦力一直保持最大靜摩擦力不變，選項C錯誤； 0＜ω≤時，A所受的摩擦力提供向心力，即Ff＝mω

12、2L，靜摩擦力隨角速度增大而增大，當＜ω＜時，以A、B整體為研究對象，F(xiàn)fA＋kmg＝mω2L＋mω2·2L，可知A所受的靜摩擦力隨角速度的增大而增大，選項D正確．] 6．如圖5所示，一宇航員站在質量分布均勻的某星球表面的一斜坡上的A點，沿水平方向以速度v0拋出一個小球，測得經過時間t小球落到斜坡上的另一點B，斜坡的傾角為θ，已知該星球的半徑為R，求： 圖5 (1)該星球表面的重力加速度； (2)該星球的第一宇宙速度. 【導學號：37162097】 【解析】　(1)設該星球表面的重力加速度為g，由平拋運動規(guī)律，則 x＝v0t y＝gt2 ＝tan θ 解得g＝. (2)一質量為m的衛(wèi)星在該星球表面附近環(huán)繞星球運行時，重力提供向心力，則 mg＝m 解得v＝＝ 即該星球的第一宇宙速度． 【答案】　(1)　(2)