《高三理科數(shù)學(xué) 二輪復(fù)習(xí)跟蹤強化訓(xùn)練：15 Word版含解析》由會員分享，可在線閱讀，更多相關(guān)《高三理科數(shù)學(xué) 二輪復(fù)習(xí)跟蹤強化訓(xùn)練：15 Word版含解析（12頁珍藏版）》請在裝配圖網(wǎng)上搜索。

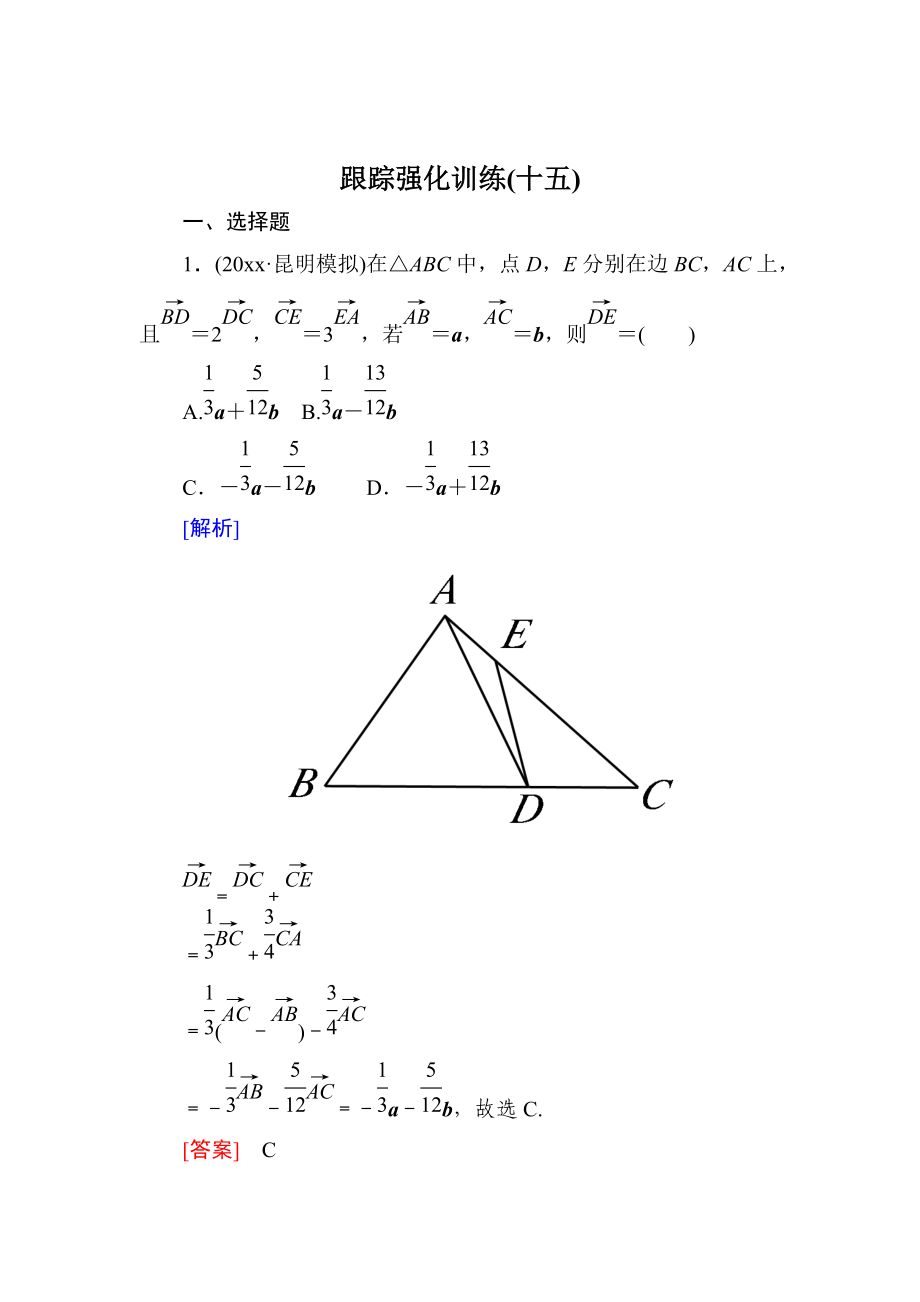
1、 跟蹤強化訓(xùn)練(十五) 一、選擇題 1．(20xx昆明模擬)在△ABC中，點D，E分別在邊BC，AC上，且＝2，＝3，若＝a，＝b，則＝(　　) A.a＋b B.a－b C．－a－b D．－a＋b [解析]　 ＝＋ ＝＋ ＝(－)－ ＝－－＝－a－b，故選C. [答案]　C 2．(20xx吉林白城模擬)已知向量a＝(2,3)，b＝(－1,2)，若ma＋nb與a－2b共線，則＝(　　) A. B．2 C．－ D．－2 [解析]　由向量a＝(2,3)，b＝(－1,2)，得ma＋nb＝(2m－n,3m＋2n)，a－2b＝(4，－1)．由ma＋nb與

2、a－2b共線，得＝，所以＝－，故選C. [答案]　C 3．(20xx廣東深圳第二次調(diào)研)如圖，正方形ABCD中，M是BC的中點，若＝λ＋μ，則λ＋μ＝(　　) A. B. C. D．2 [解析]　因為M是BC的中點，所以＝，所以＝λ＋μ ＝λ(＋)＋μ(－) ＝λ＋μ(－) ＝(λ－μ)＋ ＝＋， 即解得所以λ＋μ＝. [答案]　B 4．(20xx陜西省寶雞市高三一檢)已知向量a＝(－2，－1)，b＝(λ，1)，若a與b的夾角為鈍角，則λ的取值范圍是(　　) A.∪(2，＋∞) B．(2，＋∞) C. D. [解析]　依題意，當(dāng)a與b的夾角為鈍

3、角時，ab＝－2λ－1<0，解得λ>－.而當(dāng)a與b共線時，有－21＝－λ，解得λ＝2，即當(dāng)λ＝2時，a＝－b，a與b反向共線，a與b的夾角為π，不是鈍角，因此，當(dāng)a與b的夾角為鈍角時，λ的取值范圍是∪(2，＋∞)，選A. [答案]　A 5．(20xx云南省高三調(diào)研考試)平面向量a與b的夾角為45，a＝(1,1)，|b|＝2，則|3a＋b|等于(　　) A．13＋6 B．2 C. D. [解析]　依題意得a2＝2，ab＝2cos45＝2，|3a＋b|＝＝＝＝，選D. [答案]　D 6．(20xx西安模擬)在△ABC中，A＝120，＝－1，則||的最小值是(　　) A.

4、B．2 C. D．6 [解析]　因為＝－1，所以bccos120＝－1，即bc＝2，在△ABC中，由余弦定理得：a2＝b2＋c2－2bccos120＝b2＋c2＋bc≥3bc＝6，所以a≥，即||的最小值是. [答案]　C 7．(20xx西安質(zhì)量檢測)△ABC是邊長為2的等邊三角形，已知向量a，b滿足＝2a，＝2a＋b，則下列結(jié)論正確的是(　　) A．|b|＝1 B．a(chǎn)⊥b C．a(chǎn)b＝1 D．(4a＋b)⊥ [解析]　由題意，＝－＝(2a＋b)－2a＝b，則|b|＝2，故A錯誤；|2a|＝2|a|＝2，所以|a|＝1，又＝2a(2a＋b)＝4|a|2＋2ab＝22cos

5、60＝2，所以ab＝－1，故B，C錯誤．故應(yīng)選D. [答案]　D 8．在△ABC中，點D在線段BC的延長線上，且＝3，點O在線段CD上(與點C、D不重合)，若＝x＋(1－x)，則x的取值范圍是(　　) A. B. C. D. [解析]　依題意，設(shè)＝λ，其中1<λ<，則有 ＝＋＝＋λ＝＋λ(－)＝(1－λ)＋λ. 又＝x＋(1－x)，且，不共線，于是有x＝1－λ，由λ∈，知x∈，即x的取值范圍是. [答案]　D 9. 如圖所示，點A，B，C是圓O上的三點，線段OC與線段AB交于圓內(nèi)一點M，若＝m＋n(m>0，n>0)，m＋n＝2，則∠AOB的最小值為(　　) A.

6、 B. C. D. [解析]　解法一：由題意mn≤2＝1，將＝m＋n平方得 1＝m2＋n2＋2mncos∠AOB，cos∠AOB ＝＝＝－＋1≤－(當(dāng)且僅當(dāng)m＝n＝1時等號成立)， ∵0<∠AOB<π，∴∠AOB的最小值為. 解法二：已知AB與OC的交點為M，設(shè)λ＝＝m＋n，A，B，M三點共線，則λ＝m＋n＝2，說明M是OC的中點，在同一圓中相等弦所對的圓心角相等，且較短弦所對的圓心角也較小，可知AB⊥OC且互相平分，由平行四邊形法則，四邊形OACB是菱形，且∠AOB＝，故選D. [答案]　D 10．已知a，b是平面內(nèi)兩個互相垂直的單位向量，若向量c滿足(a－c)(b－

7、c)＝0，則|c|的最大值是(　　) A．1 B．2 C. D. [解析]　解法一：設(shè)a＝(1,0)，b＝(0,1)，c＝(x，y)，則(a－c)(b－c)＝0，即(1－x，－y)(－x,1－y)＝0， 整理得2＋2＝，這是一個圓心坐標(biāo)為，半徑為的圓，所求的值等價于這個圓上的點到坐標(biāo)原點的最大距離．根據(jù)圖形可知，這個最大距離是，即所求的最大值為. 解法二：直接把(a－c)(b－c)＝0按照數(shù)量積的運算法則展開，利用|a|＝|b|＝1，ab＝0化簡后解決． ∵|a|＝|b|＝1，ab＝0，∴由(a－c)(b－c)＝0可得|c|2＝c(a＋b)，由于a，b是平面內(nèi)兩個互相垂直的單位

8、向量，故|a＋b|＝.設(shè)a＋b與c的夾角為θ，則|c|2＝c(a＋b)＝|c||a＋b|cosθ，即|c|＝|a＋b|cosθ＝cosθ≤，所以|c|的最大值是. [答案]　C 11．(20xx鄭州適應(yīng)性測試)已知△ABC的三個頂點的坐標(biāo)為A(0,1)，B(1,0)，C(0，－2)，O為坐標(biāo)原點，動點M滿足||＝1，則|＋＋|的最大值是(　　) A.＋1 B.＋1 C.－1 D.－1 [解析]　設(shè)點M的坐標(biāo)為(x，y)，∵C(0，－2)， 且||＝1，∴＝1，即x2＋(y＋2)2＝1，∴動點M的軌跡是以C為圓心，1為半徑的圓， ∵A(0,1)，B(1,0)，∴＋＋＝(x＋

9、1，y＋1)，則|＋＋|＝，其幾何意義為動點M(x，y)與點N(－1，－1)之間的距離，即圓C上的點與點N(－1，－1)的距離，∵點N(－1，－1)在圓C外部，∴|＋＋|的最大值是||＋1＝＋1＝＋1，故選A. [答案]　A 12．已知⊥，||＝，||＝t，若點P是△ABC所在平面內(nèi)的一點，且＝＋，則的最大值等于(　　) A．13 B．15 C．19 D．21 [解析]　依題意，以點A為坐標(biāo)原點，以AB所在的直線為x軸，AC所在的直線為y軸建立如圖所示的平面直角坐標(biāo)系，如圖．因為＝＋，所以點P(1,4)，B，C(0，t)． 所以＝(－1，t－4)＝(－1)－4(t－4)＝1

10、7－－4t. 因為＋4t≥2 ＝4，所以17－－4t≤17－4＝13，所以的最大值為13，故選A. [答案]　A 二、填空題 13．(20xx全國卷Ⅰ)已知向量a，b的夾角為60，|a|＝2，|b|＝1，則|a＋2b|＝________. [解析]　由題意知ab＝|a||b|cos60＝21＝1，則|a＋2b|2＝(a＋2b)2＝|a|2＋4|b|2＋4ab＝4＋4＋4＝12. 所以|a＋2b|＝2. [答案]　2 14．(20xx南昌一模)在△ABC中，＝(，)，＝(1，)，則△ABC的面積為________． [解析]　∵||＝，||＝，＝＋， ∴cos∠BAC＝＝.

11、 ∴sin∠BAC＝ ＝ ＝. ∴S△ABC＝||||sin∠BAC＝＝. [答案]　 15．(20xx西寧模擬)如圖， 在平行四邊形ABCD中，已知AB＝8，AD＝5，＝3，＝2，則的值是________． [解析]　∵＝＋，＝－，∴＝2－－2＝2，又AB＝8，AD＝5，解得＝22. [答案]　22 16．(20xx天津卷)在△ABC中，∠A＝60，AB＝3，AC＝2.若＝2，＝λ－(λ∈R)，且＝－4，則λ的值為________． [解析]　 如圖，由＝2得＝＋， 所以＝(λ－)＝λ－2＋λ2－，又＝32cos60＝3，2＝9，2＝4，所以＝λ－3＋λ－2＝λ－5＝－4，解得λ＝. 解法二：以A為原點，AB所在的直線為x軸建立平面直角坐標(biāo)系，如圖，因為AB＝3，AC＝2，∠A＝60，所以B(3,0)，C(1，)，又＝2，所以D，所以＝，而＝λ－＝λ(1，)－(3,0)＝(λ－3，λ)，因此＝(λ－3)＋λ＝λ－5＝－4， 解得λ＝. [答案]