《2018年高考數(shù)學(xué) 第八章 立體幾何 專題30 空間向量與立體幾何考場(chǎng)高招大全.doc》由會(huì)員分享，可在線閱讀，更多相關(guān)《2018年高考數(shù)學(xué) 第八章 立體幾何 專題30 空間向量與立體幾何考場(chǎng)高招大全.doc（14頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

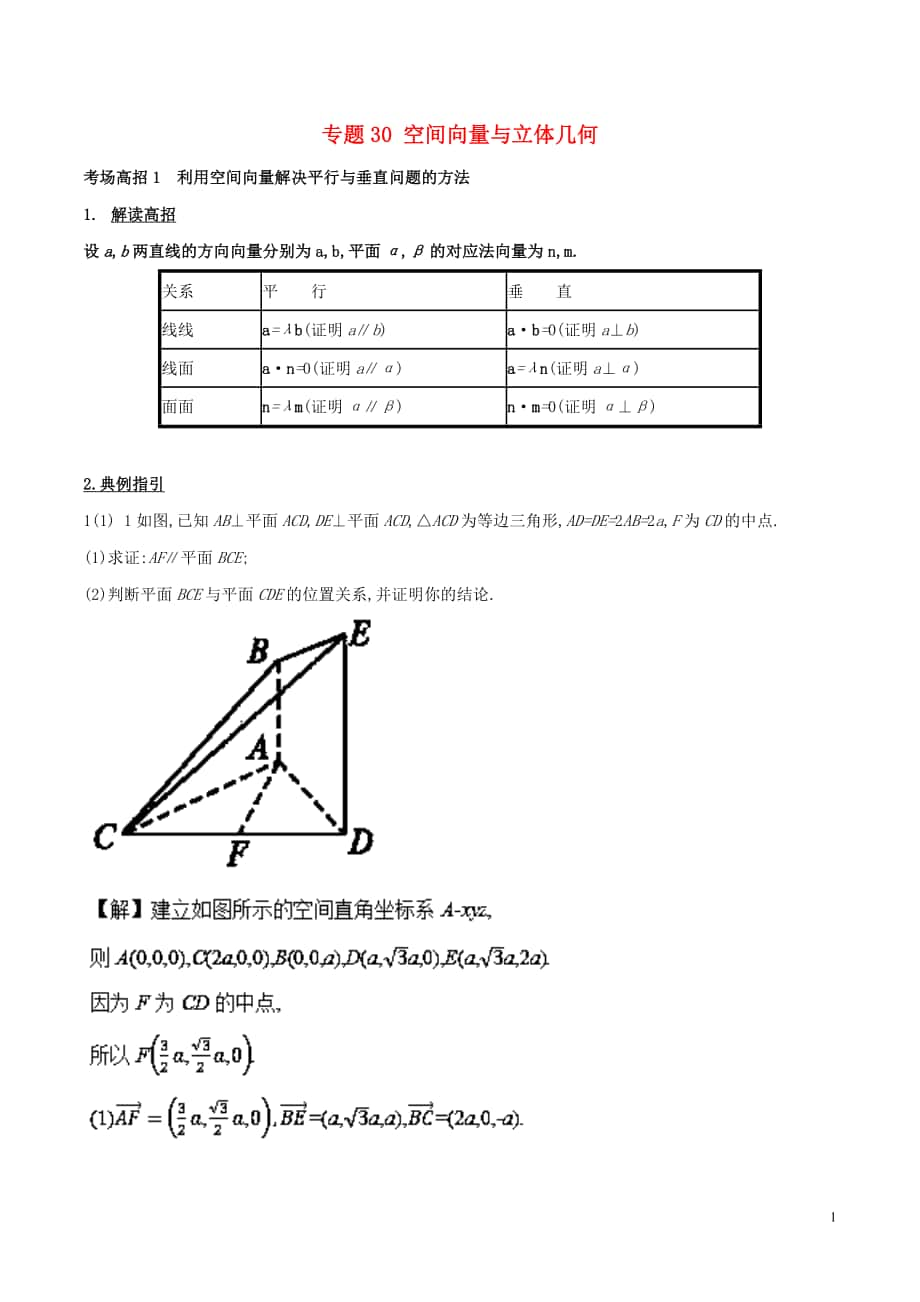
1、 專題30 空間向量與立體幾何 考場(chǎng)高招1 利用空間向量解決平行與垂直問(wèn)題的方法 1. 解讀高招 設(shè)a,b兩直線的方向向量分別為a,b,平面α,β的對(duì)應(yīng)法向量為n,m. 關(guān)系 平　　行 垂　　直 線線 a=λb(證明a∥b) a·b=0(證明a⊥b) 線面 a·n=0(證明a∥α) a=λn(證明a⊥α) 面面 n=λm(證明α∥β) n·m=0(證明α⊥β) 2.典例指引 1(1) 1如圖,已知AB⊥平面ACD,DE⊥平面ACD,△ACD為等邊三角形,AD=DE=2AB=2a,F為CD的中點(diǎn). (1)求證:AF∥平面BCE; (2)判斷平

2、面BCE與平面CDE的位置關(guān)系,并證明你的結(jié)論. D.a>b>c 考場(chǎng)高招32運(yùn)用空間向量解決立體幾何問(wèn)題的步驟 1.解讀高招 步驟 解　　讀 建系 根據(jù)題中的幾何圖形的特征建立適當(dāng)?shù)目臻g直角坐標(biāo)系 定坐標(biāo) 確定點(diǎn)的坐標(biāo)進(jìn)而求出有關(guān)向量的坐標(biāo) 向量 運(yùn)算 進(jìn)行相關(guān)的空間向量的運(yùn)算 翻譯 將向量中的語(yǔ)言“翻譯”成相應(yīng)的立體幾何中的語(yǔ)言,完成幾何問(wèn)題的求解 溫馨 提醒 在建立空間直角坐標(biāo)系求點(diǎn)的坐標(biāo)時(shí),要使盡可能多的點(diǎn)落在坐標(biāo)軸上,盡可能多的線段平行于坐標(biāo)軸,有直角的,把直角邊放在坐標(biāo)軸上 2.典例指引 2．如圖,已知四棱臺(tái)ABCD-A1B

3、1C1D1的上、下底面分別是邊長(zhǎng)為3和6的正方形,A1A=6,且A1A⊥底面ABCD,點(diǎn)P,Q分別在棱DD1,BC上. (1)若P是DD1的中點(diǎn),證明:AB1⊥PQ. (2)若PQ∥平面ABB1A1,二面角P-QD-A的余弦值為 ,求四面體ADPQ的體積. (2)由題設(shè)知,=(6,m-6,0),=(0,-3,6)是平面PQD內(nèi)的兩個(gè)不共線向量. 設(shè)n1=(x,y,z)是平面PQD的一個(gè)法向量, 則 取y=6,得n1=(6-m,6,3). 又平面AQD的一個(gè)法向量是n2=(0,0,1), 所以cos==. 而二面角P-QD-A的余弦值為,因此,解得

4、m=4,或m=8(舍去),此時(shí)Q(6,4,0). 設(shè)=λ(0<λ≤1),而=(0,-3,6),由此得點(diǎn)P(0,6-3λ,6λ),所以=(6,3λ-2,-6λ). 因?yàn)镻Q∥平面ABB1A1,且平面ABB1A1的一個(gè)法向量是n3=(0,1,0),所以·n3=0,即3λ-2=0,亦即λ=,從而P(0,4,4). 于是,將四面體ADPQ視為以△ADQ為底面的三棱錐P-ADQ,則其高h(yuǎn)=4.故四面體ADPQ的體積V=S△ADQ·h=×6×6×4=24 (2)如圖,過(guò)點(diǎn)P作PM∥A1A交AD于點(diǎn)M,則PM∥平面ABB1A1. ② 因?yàn)锳1A⊥平面ABCD,所以PM⊥平面ABCD. 過(guò)

5、點(diǎn)M作MN⊥QD于點(diǎn)N,連接PN,則PN⊥QD,∠PNM為二面角P-QD-A的平面角,所以cos∠PNM=,即,從而. 連接MQ,由PQ∥平面ABB1A1及②知,平面PQM∥平面ABB1A1,所以MQ∥AB.又ABCD是正方形,所以ABQM為矩形,故MQ=AB=6. 設(shè)MD=t,則MN=. ④ 過(guò)點(diǎn)D1作D1E∥A1A交AD于點(diǎn)E,則AA1D1E為矩形,所以D1E=A1A=6,AE=A1D1=3,因此ED=AD-AE=3. 于是=2,所以PM=2MD=2t. 再由③,④得,解得t=2,因此PM=4. 故四面體ADPQ的體積V=S△ADQ·PM=×6×6×4=24. 3.親臨

6、考場(chǎng) (2014重慶,理19)如圖,四棱錐P-ABCD中,底面是以O(shè)為中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=,M為BC上一點(diǎn),且BM=,MP⊥AP. (1)求PO的長(zhǎng); (2)求二面角A-PM-C的正弦值. (2)由(1)知,, . 設(shè)平面APM的法向量為n1=(x1,y1,z1), 平面PMC的法向量為n2=(x2,y2,z2), 由n1·=0,n1·=0, 得 故可取n1=,由n2·=0,n2·=0, 得故可取從而法向量n1,n2的夾角的余弦值為 cos==-, 故所求二面角A-PM-C的正弦值為. 考點(diǎn)69 利用空間

7、向量求空間角 考場(chǎng)高招3 三法(定義法、間接法、向量法)搞定線面角 1.解讀高招 方法 解　　讀 適合題型 典例指引 定義法 利用面面垂直的性質(zhì)定理,得到線面垂直,進(jìn)而確定線面角中的垂足.明確斜線在平面內(nèi)的射影,即可確定線面角 垂足位置易確定,順利找到線面角 典例導(dǎo) 引3(1) 幾何法 在構(gòu)成線面角的直角三角形中,可利用等體積法求解垂線段的長(zhǎng)度h,而不必畫出線面角,利用sin θ=進(jìn)行求角 垂足位置不易確定,線面角不好找 典例導(dǎo) 引3(2) 方法一 向量法 借助直線的方向向量與平面的法向量所成的角求直線與平面所成的角. 如圖所示,設(shè)l為平面α的斜線

8、,l∩α=A,a為l的方向向量,n為平面α的法向量,φ為l與α所成的角,則sin φ=|cos|= 能夠順利建立空間直角坐標(biāo)系,各點(diǎn)坐標(biāo)容易確定 典例導(dǎo) 引3(2) 方法二 2.典例指引 2(1) 3(1)在三棱錐P-ABC中,PA=PB=PC=12,∠ACB=30°, AB=6,則PB與平面ABC所成角的余弦值為　　　　　;? (2)正三棱柱ABC-A1B1C1的所有棱長(zhǎng)都相等,D是A1C1的中點(diǎn),則直線AD與平面B1DC所成角的正弦值為　　　　　.? (方法二:向量法)如圖,取AC的中點(diǎn)為坐標(biāo)原點(diǎn),建立空間直角坐標(biāo)系. 設(shè)各棱長(zhǎng)為2,則A(0,-1

9、,0),D(0,0,2),C(0,1,0),B1(,0,2). 設(shè)n=(x,y,z)為平面B1CD的法向量, 則取n=(0,2,1). 故cos<,n>=,即所求角的正弦值為. 3.親臨考場(chǎng) 1.(2017課標(biāo)Ⅱ,理19)如圖,四棱錐P-ABCD中,側(cè)面PAD為等邊三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中點(diǎn). (1)證明:直線CE∥平面PAB; (2)點(diǎn)M在棱PC上,且直線BM與底面ABCD所成角為45°,求二面角M-AB-D的余弦值. (2)由已知得BA⊥AD,以A為坐標(biāo)原點(diǎn),的方向?yàn)閤軸正方向,||為單位

10、長(zhǎng),建立如圖所示的空間直角坐標(biāo)系A(chǔ)-xyz,則A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,),=(1,0,-),=( 1,0,0). 設(shè)M(x,y,z)(0|=sin45°,, 即(x-1)2+y2-z2=0. ① 又M在棱PC上,設(shè)=λ,則 考點(diǎn)70 立體幾何的綜合問(wèn)題 考場(chǎng)高招 4解決立體幾何中的折疊問(wèn)題、最值問(wèn)題的規(guī)律 題型 方法解讀 典例指引 折疊 問(wèn)題 (1)解決與

11、折疊有關(guān)的問(wèn)題的關(guān)鍵是搞清折疊前后的變化量和不變量,一般情況下,折線同一側(cè)的,線段的長(zhǎng)度是不變量,而位置關(guān)系往往會(huì)發(fā)生變化,抓住不變量是解決問(wèn)題的突破口.(2)在解決問(wèn)題時(shí),要綜合考慮折疊前后的圖形,既要分析折疊后的圖形,也要分析折疊前的圖形 典例導(dǎo) 引5(1) 最值 問(wèn)題 求最值的途徑有很多,如利用代數(shù)知識(shí)建立函數(shù)法、由常用不等式解不等式法等都是一些常用的求最值的方法;有時(shí)也可以利用共線求距離最值 典例導(dǎo) 引5(2) 2.典例指引 4．已知長(zhǎng)方形ABCD,AB=3,AD=4.現(xiàn)將長(zhǎng)方形沿對(duì)角線BD折起,使AC=a,得到一個(gè)四面體A-BCD,如圖所示. ?(1)試問(wèn):在折

12、疊的過(guò)程中,直線AB與CD能否垂直?若能,求出相應(yīng)a的值;若不能,請(qǐng)說(shuō)明理由; (2)求四面體ABCD體積的最大值. 【解】 (1)直線AB與CD能夠垂直. 因?yàn)锳B⊥AD,若AB⊥CD,AD∩CD=D, 則AB⊥平面ACD,從而AB⊥AC. 此時(shí),a=, 即當(dāng)a=時(shí),AB⊥CD. (2)因?yàn)椤鰾CD的面積為定值,所以當(dāng)點(diǎn)A到平面BCD的距離最大,即當(dāng)平面ABD⊥平面BCD時(shí),該四面體的體積最大. 此時(shí),過(guò)點(diǎn)A在平面ABD內(nèi)作AH⊥BD,垂足為H, 則AH⊥平面BCD,AH就是該四面體的高. 在△ABD中,AH=,S△BCD=×3×4=6, 此時(shí)VA-BCD=S△BC

13、D·AH=,即為該四面體體積的最大值. 3.親臨考場(chǎng) 1. (2017課標(biāo)Ⅰ,理16)如圖,圓形紙片的圓心為O,半徑為5 cm,該紙片上的等邊三角形ABC的中心為O.D,E,F為圓O上的點(diǎn),△DBC,△ECA, △FAB分別是以BC,CA,AB為底邊的等腰三角形,沿虛線剪開后,分別以BC,CA,AB為折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱錐.當(dāng)△ABC的邊長(zhǎng)變化時(shí),所得三棱錐體積(單位:cm3)的最大值為　　　　　　. 所以三棱錐的體積V=S△ABC·h =x2·. 令f(x)=25x4-10x5,x∈,則f'(x)=100x3-50x4.

14、令f'(x)=0,可得x=2,則f(x)在(0,2)單調(diào)遞增,在單調(diào)遞減,所以f(x)max=f(2)=80. 所以V≤=4,所以三棱錐體積的最大值為4 2.(2017課標(biāo)Ⅲ,理16)a,b為空間中兩條互相垂直的直線,等腰直角三角形ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉(zhuǎn)軸旋轉(zhuǎn),有下列結(jié)論: ①當(dāng)直線AB與a成60°角時(shí),AB與b成30°角; ②當(dāng)直線AB與a成60°角時(shí),AB與b成60°角; ③直線AB與a所成角的最小值為45°; ④直線AB與a所成角的最大值為60°. 其中正確的是　　　　　.(填寫所有正確結(jié)論的編號(hào)) 【答案】 ②③ 14