《精修版山東省高中數(shù)學(xué)新課標(biāo)人教A版必修三第3章 概率導(dǎo)學(xué)案》由會(huì)員分享，可在線閱讀，更多相關(guān)《精修版山東省高中數(shù)學(xué)新課標(biāo)人教A版必修三第3章 概率導(dǎo)學(xué)案（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

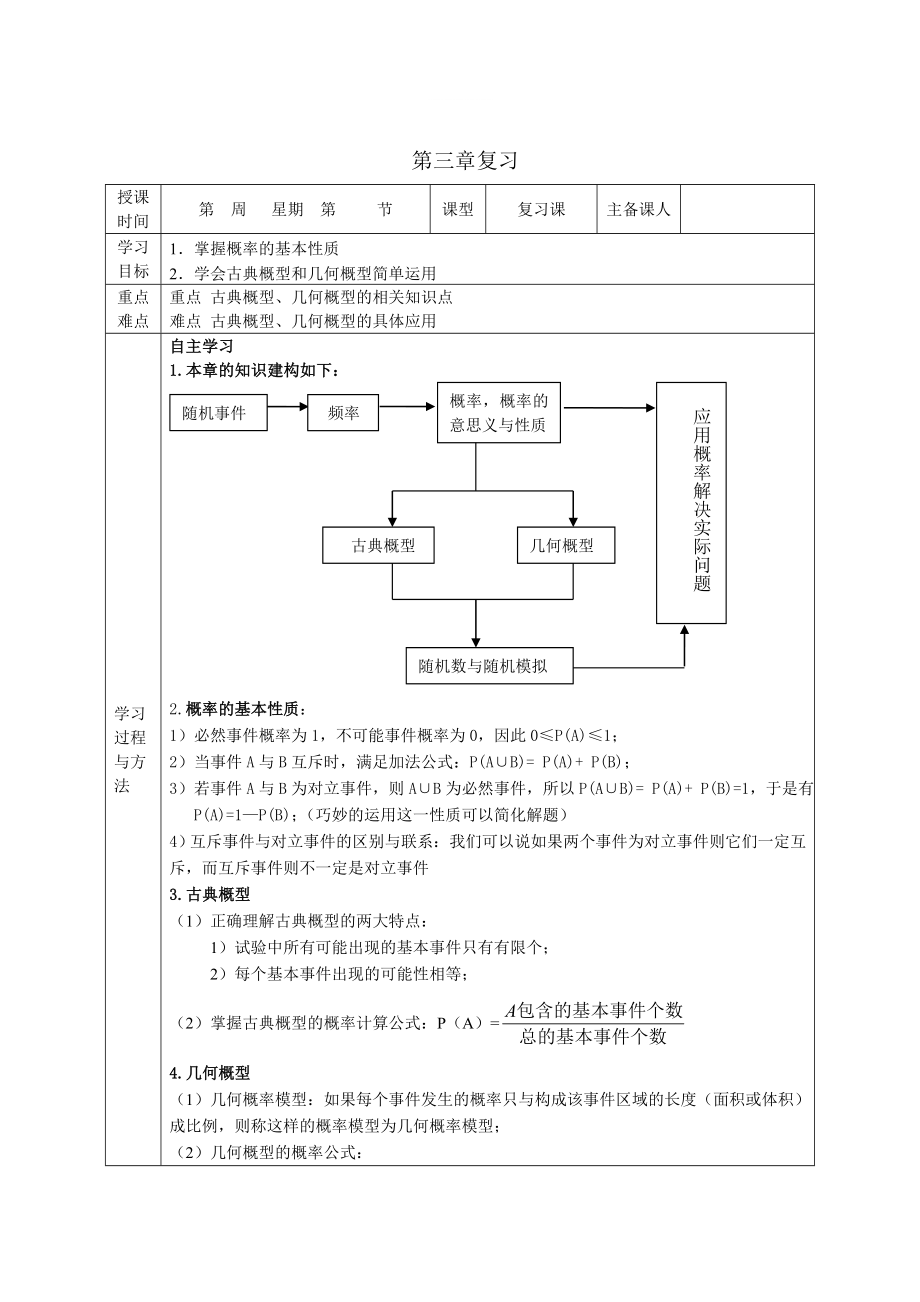
1、精修版資料整理精修版資料整理精修版資料整理精修版資料整理精修版資料整理精修版資料整理 第三章復(fù)習(xí) 授課 時(shí)間 第 周 星期 第 節(jié) 課型 復(fù)習(xí)課 主備課人 學(xué)習(xí) 目標(biāo) 1．掌握概率的基本性質(zhì) 2．學(xué)會(huì)古典概型和幾何概型簡(jiǎn)單運(yùn)用 重點(diǎn)難點(diǎn) 重點(diǎn) 古典概型、幾何概型的相關(guān)知識(shí)點(diǎn) 難點(diǎn) 古典概型、幾何概型的具體應(yīng)用 學(xué)習(xí) 過(guò)程 與方 法 自主學(xué)習(xí) 1.本章的知識(shí)建構(gòu)如下： 隨機(jī)事件 頻率 概率，概率的意思義與性質(zhì) 應(yīng)用概率解決實(shí)際問(wèn)題 古典概型 幾何概型 隨機(jī)數(shù)與隨機(jī)模擬 2.概率的基本性質(zhì)： 1）必然事件概率

2、為1，不可能事件概率為0，因此0≤P(A)≤1； 2）當(dāng)事件A與B互斥時(shí)，滿(mǎn)足加法公式：P(A∪B)= P(A)+ P(B)； 3）若事件A與B為對(duì)立事件，則A∪B為必然事件，所以P(A∪B)= P(A)+ P(B)=1，于是有P(A)=1—P(B)；（巧妙的運(yùn)用這一性質(zhì)可以簡(jiǎn)化解題） 4）互斥事件與對(duì)立事件的區(qū)別與聯(lián)系：我們可以說(shuō)如果兩個(gè)事件為對(duì)立事件則它們一定互斥，而互斥事件則不一定是對(duì)立事件 3.古典概型 （1）正確理解古典概型的兩大特點(diǎn)： 1）試驗(yàn)中所有可能出現(xiàn)的基本事件只有有限個(gè)； 2）每個(gè)基本事件出現(xiàn)的可能性相等； （2）掌握古典概型的概率計(jì)算公式：P（A）=

3、4.幾何概型 （1）幾何概率模型：如果每個(gè)事件發(fā)生的概率只與構(gòu)成該事件區(qū)域的長(zhǎng)度（面積或體積）成比例，則稱(chēng)這樣的概率模型為幾何概率模型； （2）幾何概型的概率公式： P（A）=； （3）幾何概型的特點(diǎn)：1）試驗(yàn)中所有可能出現(xiàn)的結(jié)果（基本事件）有無(wú)限多個(gè)； 2）每個(gè)基本事件出現(xiàn)的可能性相等． 5.古典概型和幾何概型的區(qū)別 相同：兩者基本事件的發(fā)生都是等可能的； 不同：古典概型要求基本事件有有限個(gè)， 幾何概型要求基本事件有無(wú)限多個(gè). 精講互動(dòng) 例1、柜子里裝有3雙不同的鞋，隨機(jī)地取出2只，試求下列事件的概率 （1）取出的鞋子都是左腳的; （2）取出的鞋子都是同一只腳的 （選作）變式：（1）取出的鞋一只是左腳的，一只是右腳的； （2）取出的鞋不成對(duì) 例2、取一根長(zhǎng)為3 m的繩子，拉直后在任意位置剪斷，那么剪得兩段的長(zhǎng)度都不小于1m的概率有多大？ 達(dá)標(biāo)訓(xùn)練 1. 課本p161 復(fù)習(xí)題三 A組：1 2 3 4 5 6 2. 教輔資料 作業(yè) 布置 1.復(fù)習(xí)題三 A組：7 、8、 9、 10 、11 2.教輔資料 學(xué)習(xí)小結(jié)/教學(xué) 反思 最新精品資料