《2018年七年級升八年級數(shù)學 暑期銜接班講義 第八講 全等三角形的判定（二）SSSASAAAS（無答案） 新人教版》由會員分享，可在線閱讀，更多相關《2018年七年級升八年級數(shù)學 暑期銜接班講義 第八講 全等三角形的判定（二）SSSASAAAS（無答案） 新人教版（8頁珍藏版）》請在裝配圖網(wǎng)上搜索。

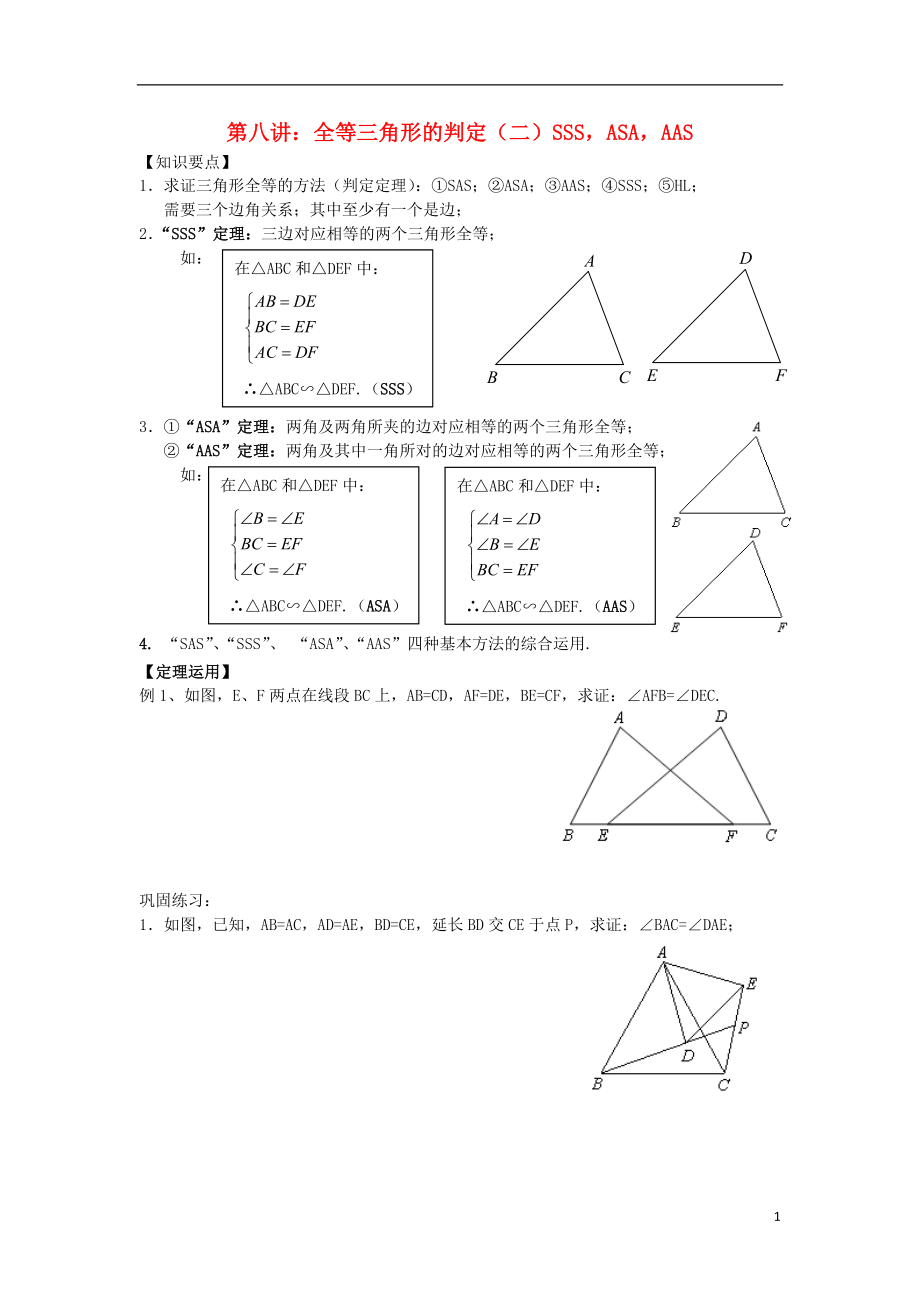
1、 第八講：全等三角形的判定（二）SSS，ASA，AAS 【知識要點】 1．求證三角形全等的方法（判定定理）：①SAS；②ASA；③AAS；④SSS；⑤HL； 需要三個邊角關系；其中至少有一個是邊； 2．“SSS”定理：三邊對應相等的兩個三角形全等； 在△ABC和△DEF中： ∴△ABC∽△DEF.（SSS） 如： 3．①“ASA”定理：兩角及兩角所夾的邊對應相等的兩個三角形全等； ②“AAS”定理：兩角及其中一角所對的邊對應相等的兩個三角形全等； 在△ABC和△DEF中： ∴△ABC∽△DEF.（ASA）

2、在△ABC和△DEF中： ∴△ABC∽△DEF.（AAS） 如： 4. “SAS”、“SSS”、 “ASA”、“AAS”四種基本方法的綜合運用. 【定理運用】 例1、如圖，E、F兩點在線段BC上，AB=CD，AF=DE，BE=CF，求證：∠AFB=∠DEC. 鞏固練習： 1．如圖，已知，AB=AC，AD=AE，BD=CE，延長BD交CE于點P，求證：∠BAC=∠DAE； 例2.已知命題：如圖，點A，D，B，E在同一條直線上，且AD=BE，BC=EF，則△ABC≌△DEF.（

3、1）判斷這個命題是真命題還是假命題？ （2）如果是真命題，請給出證明；如果是假命題，請?zhí)砑右粋€適當條件使它成為真命題,并能運用“SSS”公理加以證明. 鞏固練習： 1.如圖，已知，AB=CD，BE=DF，AF=CE，求證：AD∥BC. 2.已知：如圖，AB=AC，AD=AE，∠1=∠2，求證：AF=AG. 例3.、如圖，C為線段AB的中點，AD∥CE，∠D=∠E，求證：CD=EB. 鞏固練習 1.如圖，AD為△ABC的高線，E、F為直線AD上兩點，DE=DF，BE∥CF，求證：AB

4、=AC. 2.如圖，∠ABC=∠DCB，BD、CA分別是∠ABC、∠DCB的平分線，求證：AB=DC. 例4.如圖，△ABC中，AB=AC，D、E分別在BC、AC的延長線上，∠1=∠2=∠3，求證：AD=AE. 鞏固練習： 1.已知：如圖，∠A=∠D，OA=OD，求證：∠1=∠2. 2.已知：AD∥BC，AE⊥BD，CF⊥BD，AE=CF，求證：AB=CD. 例5.已知：如圖，AB=CD，∠A=∠D，求證：∠ABC=∠DCB. 鞏

5、固練習：1.已知：如圖，AB=AC，AD=AE，求證：∠DBC=∠ECB. 2.已知：如圖，△ABC中，∠BAC=∠BCA，延長BC邊的中線AD到E點，使AD=DE，F(xiàn)為BC延長線上一點，且CE=CF， 求證：AF=2AD. 例6.在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD，AC、BD交于點P. （1）①如圖1，∠AOB=∠COD=60°，則∠APD= ，AC與BD的數(shù)量關系是 ； ②如圖2，∠AOB=∠COD=90°，則∠APD= ，AC與BD的數(shù)量關系是

6、 ； （2）如圖3，∠AOB=∠COD=α°，則∠APD的度數(shù)為 （用含α的式子表示），AC與BD之間的等量關系是 ；填寫你的結論，并給出你的證明； 圖1 圖2 圖3 鞏固練習：點C為線段AB上一點，分別以AC、BC為腰在直線AB的同側作等腰△ACD和等腰△BCE，且CA=CD，CB=CE，∠ACD=∠BCE，直線AE、BD交于點F. （1）如圖1，若∠ACD=60°，則∠AFB=

7、 ； （2）如圖2，若∠ACD=°，則∠AFB= ；（用的代數(shù)式表示） （3）如圖3，將圖2中的△ACD繞點C順時針旋轉一個角度，延長BD交線段AE于點F，試探究∠AFB與之間的數(shù)量關系，并給出你的證明. 例7.已知：AB=AC，AD=AE，AF⊥CD，AG⊥BE，求證：AF=AG. 鞏固練習：1.如圖，在△ABC和△DCB中，AB = DC，AC = DB，AC與DB交于點M. （1）求證：△ABC≌△DCB ； B C A

8、 D M N （2）過點C作CN∥BD，過點B作BN∥AC，CN與BN交于點N，試判斷線段BN與CM的數(shù)量關系，并證明你的結論． 2.如圖，已知，AB=AD，AC=AE，∠1=∠2. （1）求證：BC=DE； （2）若AF平分∠BAC，求證：AF=AC. 3.已知：如圖，AB=AC，AD=AE，求證：AO平分∠BAC. 4.如圖，等腰Rt△ABC中，AB=AC，過A任作直線，BD⊥于點D，CE⊥于點E. (1) 若與BC不相交，求證：BD+CE=DE；

9、 (2) 當直線繞A點旋轉到與BC相交時，其它條件不變，試猜想BD、CE和DE的關系？ 畫圖并給出證明. 課后作業(yè)： 1．如圖，等腰Rt△ABC和等腰Rt△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°. （1）求證：BD=CE； （2）求證：BD⊥CE. 2．已知：如圖，AB=AC，AD=AE，BD=CE，求證：∠BAE=∠CAD. 3．如圖，四邊形ABCD中，AB=CD，AD=BC，求證：AB∥CD，AD∥BC. 4．已知：如圖，在四邊形ABCD中，AB=

10、CB，AD=CD，求證：∠A=∠C. 5．已知：如圖，AD=BC，AC=BD，求證:∠D=∠C. 6．如圖1，等腰△ABC中AB=AC，D、E分別在AC、AB上，且AD、AE，M、N分別BE、CD的中點. （1）CD BE，AM AN；（填“＞”、“=”、“＜”） （2）如圖2，把圖1中的△ADE繞A點逆時針旋轉任意一個角度，（1）中的兩個結論是否仍然成立？若成立請證明，若不成立請說明理由． 7．如圖，已知點E、C在線段BF上，BE=CF，AB∥DE，∠ACB=∠F. 求證：△A

11、BC∽△DEF． 8．如圖，點B、F、C、E在同一條直線上，點A、點D在直線BE的兩側，AB∥DE，AC∥DF，BF=CE，求證：AC=DF． 9．如圖，AB∥CD，AB=CD，求證：O為AC的中點. 10．如圖，在△ABC中，AD是中線，分別過點B、C作AD及其延長線的垂線BE、CF，垂足分別為點E、F，求證：BE=CF． 11．如圖，四邊形ABCD中，AB∥CD，AD∥BC，求證：AB=CD，AD=BC. 12．如圖，在△ABC中，∠C=90°，點D是AB邊上一點，DM⊥AB且DM=AC，過點M作ME∥BC交AB于點E，求證：△ABC≌△MED. 14．如圖，在△ABC中，D是BC邊的中點，F(xiàn)、E分別是AD及 其延長線上的點，請你添加一個條件，使△BDE≌△CDF (不再添加其它線段)，并能用“ASA”或 “AAS”公理進行證明． （1）你添加的條件是： ； （2）證明： 8