《2018年秋九年級數(shù)學(xué)上冊 第23章 圖形的相似 23.4 中位線同步練習(xí) （新版）華東師大版》由會員分享，可在線閱讀，更多相關(guān)《2018年秋九年級數(shù)學(xué)上冊 第23章 圖形的相似 23.4 中位線同步練習(xí) （新版）華東師大版（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

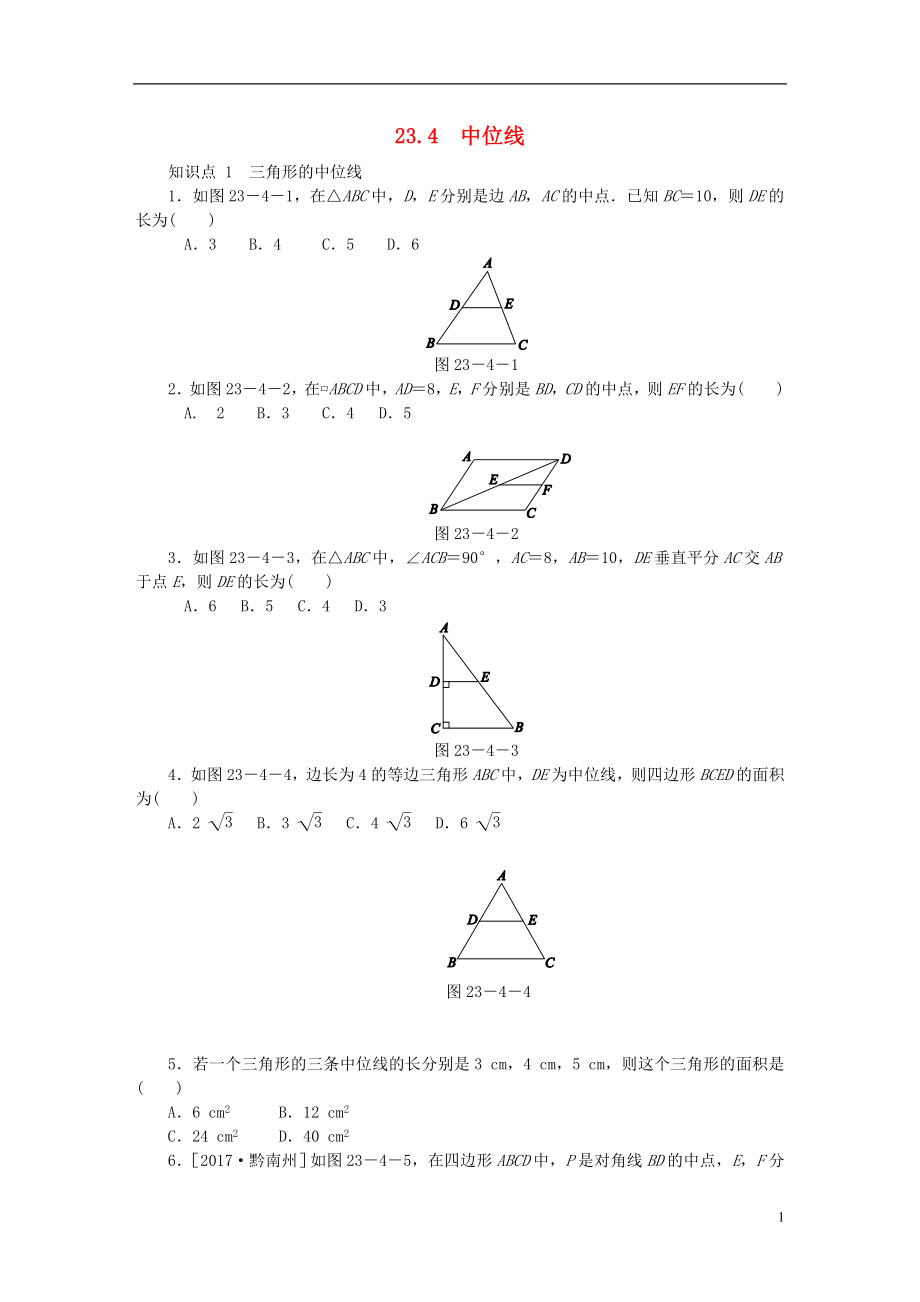
1、 23.4　中位線 知識點 1　三角形的中位線 1．如圖23－4－1，在△ABC中，D，E分別是邊AB，AC的中點．已知BC＝10，則DE的長為(　　) A．3 B．4 C．5 D．6 圖23－4－1 2．如圖23－4－2，在?ABCD中，AD＝8，E，F(xiàn)分別是BD，CD的中點，則EF的長為(　　) A. 2 B．3 C．4 D．5 　　　 圖23－4－2 3．如圖23－4－3，在△ABC中，∠ACB＝90°，AC＝8，AB＝10，DE垂直平分AC交AB于點E，則DE的長為(　　) A．6 B．5 C．4 D．3

2、 圖23－4－3 4．如圖23－4－4，邊長為4的等邊三角形ABC中，DE為中位線，則四邊形BCED的面積為(　　) A．2 B．3 C．4 D．6 　　　 圖23－4－4 5．若一個三角形的三條中位線的長分別是3 cm，4 cm，5 cm，則這個三角形的面積是(　　) A．6 cm2 B．12 cm2 C．24 cm2 D．40 cm2 6．［2017·黔南州］如圖23－4－5，在四邊形ABCD中，P是對角線BD的中點，E，F(xiàn)分別是AB，CD的中點，AD＝BC，∠FPE＝100°，則∠PFE＝________°.

3、 圖23－4－5 7．［2016·南京］如圖23－4－6，AB，CD相交于點O，OC＝2，OD＝3，AC∥BD，EF是△ODB的中位線，且EF＝2，則AC的長為________． 圖23－4－6 8．如圖23－4－7，在△ABC中，D，E，F(xiàn)分別是邊AB，BC，CA的中點，且AB＝6 cm，AC＝8 cm，則四邊形ADEF的周長為________ cm. 　　　　 圖23－4－7 9．如圖23－4－8，已知△ABC中，D，E，F(xiàn)分別為AB，BC，CA邊的中點． 求證：△DEF∽△CAB，且相似比為1∶2.　 圖23－4－8

4、 知識點 2　三角形的重心 10．在△ABC中，AD是BC邊上的中線，G是重心，則AG＝________DG.如果AG＝6，那么線段DG＝________． 11．如圖23－4－9，△ABC中，D，E分別為AB，AC的中點，連結(jié)DE，線段BE，CD相交于點O.若OD＝2，則OC＝________． 圖23－4－9 12．在△ABC中，如果AB＝AC＝5 cm，BC＝8 cm，那么這個三角形的重心G到BC的距離是________． 13．如圖23－4－10，在矩形ABCD中，P，R分別是BC和DC上的點，E，F(xiàn)分別是AP，RP的中點，當(dāng)點P在BC上從點B

5、向點C移動，而點R不動時，下列結(jié)論正確的是(　　) A．線段EF的長逐漸增長 B．線段EF的長逐漸減小 C．線段EF的長始終不變 D．線段EF的長與點P的位置有關(guān) 圖23－4－10 14．［2016·陜西］如圖23－4－11，在△ABC中，∠ABC＝90°，AB＝8，BC＝6.若DE是△ABC的中位線，延長DE交△ABC的外角∠ACM的平分線于點F，則線段DF的長為(　　) A．7 B．8 C．9 D．10 圖23－4－11 15．如圖23－4－12，在△ABC中，AB＝AC＝17，BC＝16，M是△ABC的重心，則AM的長為________. 　　　

6、 圖23－4－12 16．［如圖23－4－13，在△A1B1C1中，已知A1B1＝7，B1C1＝4，A1C1＝5，依次連結(jié)△A1B1C1的三邊中點，得△A2B2C2，再依次連結(jié)△A2B2C2的三邊中點，得△A3B3C3，…，依次進行下去，則△A5B5C5的周長為________． 圖23－4－13 17．［2017·天津］如圖23－4－14，正方形ABCD和正方形EFCG的邊長分別為3和1，點F，G分別在邊BC，CD上，P為AE的中點，連結(jié)PG，則PG的長為________． 　　 圖23－4－14 18．如圖23－4－15，已知△ABC，AD平分∠BAC交

7、BC于點D，BC的中點為M，ME∥AD，交BA的延長線于點E，交AC于點F. (1)求證：AE＝AF； (2)求證：BE＝(AB＋AC)． 圖23－4－15 19．問題探究如圖23－4－16所示，在四邊形ABCD中，E，F(xiàn)，G，H分別為各邊的中點，順次連結(jié)E，F(xiàn)，G，H，把四邊形EFGH稱為中點四邊形．連結(jié)AC，BD，容易證明：中點四邊形EFGH一定是平行四邊形． (1)如果改變原四邊形ABCD的形狀，那么中點四邊形的形狀也隨之改變，通過探索可以發(fā)現(xiàn)：當(dāng)四邊形ABCD的對角線滿足AC＝BD時，四邊形EFGH為菱形． ①當(dāng)四邊形ABCD的對角線滿足什么

8、條件時，四邊形EFGH為矩形？ ②當(dāng)四邊形ABCD的對角線滿足什么條件時，四邊形EFGH為正方形？ (2)探索△AEH，△CFG與四邊形ABCD的面積之間的等量關(guān)系，請寫出你發(fā)現(xiàn)的結(jié)論，并加以證明． 圖23－4－16 1．C　[解析] 根據(jù)三角形的中位線定理，可得DE＝BC＝5. 2．C　[解析] ∵四邊形ABCD是平行四邊形，∴BC＝AD＝8.∵E，F(xiàn)分別是BD，CD的中點，∴EF＝BC＝×8＝4.故選C. 3．D　4.B　5.C 6．40　[解析] ∵P是對角線BD的中點，E是AB的中點，∴EP＝AD，同理，F(xiàn)P＝BC. ∵AD＝BC，∴EP＝FP，∴∠PFE＝

9、∠PEF.∵∠FPE＝100°，∴∠PFE＝40°. 7. 　8. 14 9．證明：∵D，F(xiàn)分別是AB，CA的中點， ∴DF＝BC. 同理可得，DE＝CA，EF＝AB， ∴＝＝＝， ∴△DEF∽△CAB，且相似比為1∶2. 10．2　3　11.4 12．1 cm　[解析] △ABC是等腰三角形，底邊上的高為＝3(cm)，故重心G到BC的距離是3×＝1(cm)． 13．C　[解析] 連結(jié)AR.∵矩形ABCD固定不變，點R在CD上的位置不變， ∴AD和DR的長不變．由勾股定理得：AR＝，∴AR的長不變． ∵E，F(xiàn)分別為AP，RP的中點，∴EF＝AR，即線段EF的長始終不變．

10、 故選C. 14． B　[解析] 在Rt△ABC中，∵∠ABC＝90°，AB＝8，BC＝6, ∴AC＝＝＝10. ∵DE是△ABC的中位線， ∴DF∥BM，DE＝BC＝3， ∴∠EFC＝∠FCM. ∵CF平分∠ACM，∴∠FCE＝∠FCM， ∴∠EFC＝∠FCE， ∴EF＝EC＝AC＝5， ∴DF＝DE＋EF＝3＋5＝8. 故選B. 15．10. 16． 1　 17.　 18． 證明：(1)∵AD平分∠BAC， ∴∠BAD＝∠CAD. ∵AD∥EM， ∴∠BAD＝∠AEF，∠CAD＝∠AFE， ∴∠AEF＝∠AFE，∴AE＝AF. (2)如圖，過點

11、C作CG∥EM，交BA的延長線于點G. ∵EF∥CG，∴∠G＝∠AEF， ∠ACG＝∠AFE. ∵∠AEF＝∠AFE， ∴∠G＝∠ACG，∴AG＝AC. ∵BM＝CM，EM∥CG，∴BE＝EG， ∴BE＝BG＝(AB＋AG)＝(AB＋AC)． 19．解：(1)①AC⊥BD.②AC＝BD且AC⊥BD. (2)結(jié)論：S△AEH＋S△CFG＝S四邊形ABCD. 證明：∵四邊形EFGH是四邊形ABCD的中點四邊形， 由題意可知，EH是△ABD的中位線， ∴EH BD，∴△AEH∽△ABD， 可得＝＝，∴S△AEH＝S△ABD. 同理可得S△CFG＝S△CBD. ∴S△AEH＋S△CFG＝(S△ABD＋S△CBD)＝S四邊形ABCD. 7