《2018中考數(shù)學(xué)專題復(fù)習(xí) 二次函數(shù) 一題多問(無答案)》由會員分享�,可在線閱讀,更多相關(guān)《2018中考數(shù)學(xué)專題復(fù)習(xí) 二次函數(shù) 一題多問(無答案)(2頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
1���、
二次函數(shù)一題多問
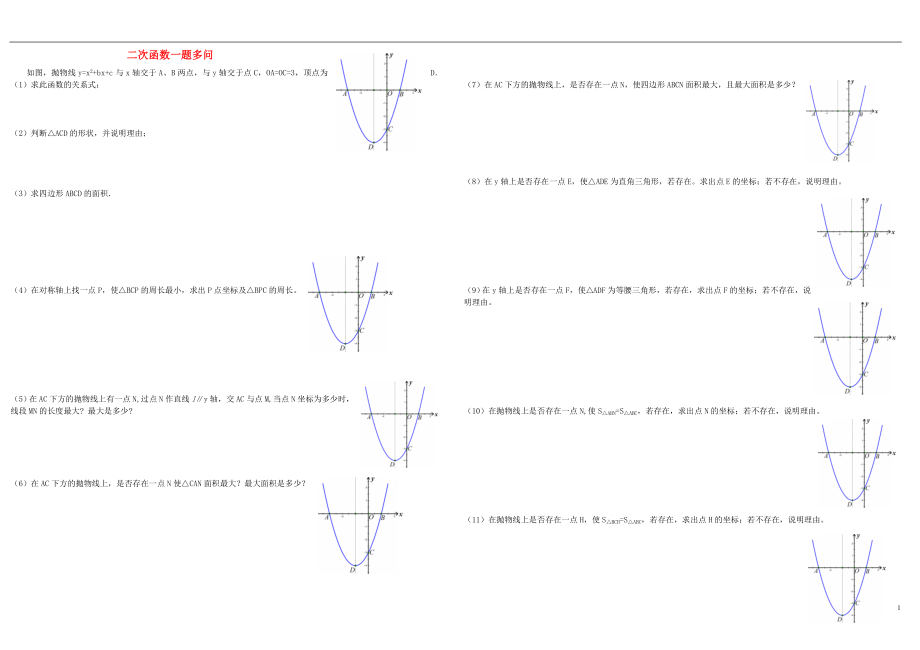
如圖,拋物線y=x2+bx+c與x軸交于A���、B兩點�,與y軸交于點C,OA=OC=3��,頂點為D.
(1)求此函數(shù)的關(guān)系式�;
(2)判斷△ACD的形狀,并說明理由�;
(3)求四邊形ABCD的面積.
(4)在對稱軸上找一點P,使△BCP的周長最小��,求出P點坐標(biāo)及△BPC的周長��。
(5)在AC下方的拋物線上有一點N,過點N作直線l∥y軸�,交AC與點M,當(dāng)點N坐標(biāo)為多少時,線段MN的長度最大? 最大是多少?
(6)在AC下方的拋物線上�,是否存在一點N使△CAN
2、面積最大�?最大面積是多少?
(7)在AC下方的拋物線上�,是否存在一點N,使四邊形ABCN面積最大�,且最大面積是多少?
(8)在y軸上是否存在一點E�,使△ADE為直角三角形���,若存在�。求出點E的坐標(biāo);若不存在��,說明理由��。
(9)在y軸上是否存在一點F�,使△ADF為等腰三角形,若存在�,求出點F的坐標(biāo);若不存在���,說明理由��。
(10)在拋物線上是否存在一點N,使S△ABN=S△ABC���,若存在,求出點N的坐標(biāo)���;若不存在��,說明理由��。
3��、
(11)在拋物線上是否存在一點H���,使S△BCH=S△ABC���,若存在,求出點H的坐標(biāo)���;若不存在�,說明理由�。
(12) 在拋物線上是否存在一點Q,使S△AOQ=S△COQ, 若存在��,求出點Q的坐標(biāo)��;若不存在��,說明理由�。
(13) 在拋物線上是否存在一點E,使BE平分△ABC的面積, 若存在���,求出點E的坐標(biāo)��;若不存在��,說明理由��。
(14)在拋物線上找一點F��,做FM⊥X軸�,交AC與點H�,使AC平分△AFM的面積?
(15)在對稱軸上有一
4��、點K���,在拋物線上有一點L��,若使A,B,K,L為頂點形成平行四邊形�,求出K,L點的坐標(biāo)���。
(16)作垂直于x軸的直線x=-1�,交直線AC于點M,交拋物線于點N���,以A,M,N,E為頂點作平行四邊形���,求第四個頂點E的坐標(biāo)。
(17)在拋物線上能不能找到一點P���,使∠POC=∠PCO�?若能,請求出點P的坐標(biāo)�;若不能,請說明理由.
(18)在線段AC上是否存在點M�,使△AOM與△ABC相似?若存在���,求出點M的坐標(biāo)�;若不存在�,說明理由.
(19)點P是拋物線上一個動點,作PH⊥x軸于H���,是否存在點P��,使得△PAH與△OBC相似��?若存在��,求出點M的坐標(biāo)�;若不存在��,說明理由.
(20)若點P從點A出發(fā)向B運動,同時點Q從點O出發(fā)向C運動���,當(dāng)一點到達終點時�,另一點也停止運動���,設(shè)運動的時間為t秒,△OPQ的面積為S��,求S與t的函數(shù)關(guān)系式�,并求出S的最大值.
2
 2018中考數(shù)學(xué)專題復(fù)習(xí) 二次函數(shù) 一題多問(無答案)
2018中考數(shù)學(xué)專題復(fù)習(xí) 二次函數(shù) 一題多問(無答案)