《安徽省2019中考數(shù)學(xué)決勝一輪復(fù)習(xí) 第6章 圓 第1節(jié) 圓的基本性質(zhì)習(xí)題》由會員分享，可在線閱讀，更多相關(guān)《安徽省2019中考數(shù)學(xué)決勝一輪復(fù)習(xí) 第6章 圓 第1節(jié) 圓的基本性質(zhì)習(xí)題（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

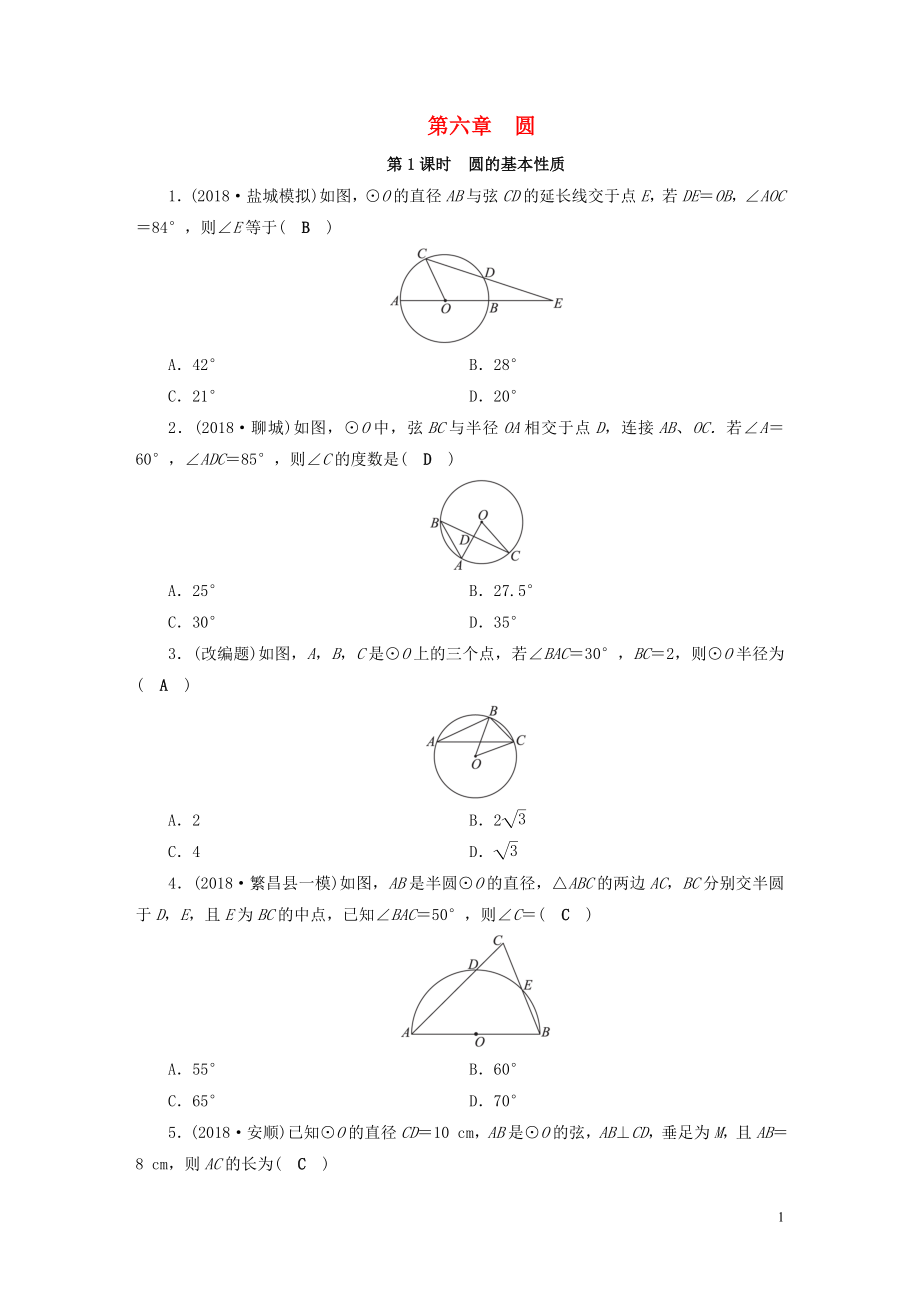
1、第六章　圓 第1課時　圓的基本性質(zhì) 1．(2018·鹽城模擬)如圖，⊙O的直徑AB與弦CD的延長線交于點E，若DE＝OB，∠AOC＝84°，則∠E等于(　B　) A．42° B．28° C．21° D．20° 2．(2018·聊城)如圖，⊙O中，弦BC與半徑OA相交于點D，連接AB、OC．若∠A＝60°，∠ADC＝85°，則∠C的度數(shù)是(　D　) A．25° B．27.5° C．30° D．35° 3．(改編題)如圖，A，B，C是⊙O上的三個點，若∠BAC＝30°，BC＝2，則⊙O半徑為(　A　) A．2 B．2 C．4 D． 4．(2018

2、·繁昌縣一模)如圖，AB是半圓⊙O的直徑，△ABC的兩邊AC，BC分別交半圓于D，E，且E為BC的中點，已知∠BAC＝50°，則∠C＝(　C　) A．55° B．60° C．65° D．70° 5．(2018·安順)已知⊙O的直徑CD＝10 cm，AB是⊙O的弦，AB⊥CD，垂足為M，且AB＝8 cm，則AC的長為(　C　) A．2 cm B．4 cm C．2 cm或4 cm D．2 cm或4 cm 6．如圖，在Rt△ABC中，∠ACB＝90°，∠A＝56°.以BC為直徑的⊙O交AB于點D，E是⊙O上一點，且＝，連接OE.過點E作EF⊥OE，交AC的延長線于點F，則∠

3、F的度數(shù)為(　C　) A．92° B．108° C．112° D．124° 7．(改編題)如圖，點A，B是⊙O上兩點，AB＝10，點P是⊙O上的動點(P與A，B不重合)連接AP，PB，過點O分別作OE⊥AP于點E，OF⊥PB于點F，則下列結(jié)論正確的是(　C　) A．EF＝2.5 B．EF＝ C．EF＝5 D．EF的長度隨P點的變化而變化 8．(2018·北京)如圖，點A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，則∠ADB＝__70__°. 9．(2018·無錫)如圖，點A，B，C都在⊙O上，OC⊥OB，點A在劣弧BC上，且OA＝AB，則∠

4、ABC＝__15__°. 10．(2018·定遠(yuǎn)縣一模)如圖，AB是半圓的直徑，∠BAC＝20°，D是的中點，則∠DAC的度數(shù)是__35°__. 11．(原創(chuàng)題)如圖，四邊形ABCD內(nèi)接于⊙O，對角線AC與BD相交于點E，F(xiàn)在AC上，AB＝AD，∠BFC＝∠BAD＝2∠DFC，下列結(jié)論： ①線段AC為⊙O的直徑；②CD⊥DF；③BC＝2CD；④∠AFB＝∠BCD．其中正確的有__②③④__(只填序號)． 12．(原創(chuàng)題)如圖，⊙O的直徑為10 cm，點C為半圓AB上任意一點，CD平分∠ACB交⊙O于點D，求AD的長． 解：∵AB為⊙O的直徑，∴∠ACB＝∠ADB＝90

5、°，而CD平分∠ACB交⊙O于點D，∴∠ACD＝∠DCB＝45°，∴∠ABD＝∠DAB＝45°，∴△ADB為等腰直角三角形，∴AD＝AB，又∵AB＝10 cm，∴AD＝5(cm)． 13．(2018·利辛縣一模)如圖，AB是半圓的直徑，O是圓心，C是半圓上一點，D是弧AC中點，OD交弦AC于E，連接BE，若AC＝8，DE＝2. 求：(1)求半圓的半徑長； (2)BE的長度． 解：(1)設(shè)圓的半徑為r，∵D是弧AC中點，∴OD⊥AC，AE＝AC＝4，在Rt△AOE中，OA2＝OE2＋AE2，即r2＝(r－2)2＋42，解得r＝5，即圓的半徑為5； (2)連接BC，∵AO＝OB，AE

6、＝EC，∴BC＝2OE＝6，∵AB是半圓的直徑，∴∠ACB＝90°，∴BE＝＝2. 14．如圖，A，B，C為⊙O上的點，PC過O點，交⊙O于D點，PD＝OD，若OB⊥AC于E點． (1)判斷A是否是PB的中點，并說明理由； (2)若⊙O半徑為8，試求BC的長． 解：(1)A是PB的中點，理由：連接AD，∵CD是⊙O的直徑，∴AD⊥AC，∵OB⊥AC，∴AD∥OB，∵PD＝OD，∴PA＝AB，∴A是PB的中點； (2)∵AD∥OB，∴△APD∽△BPO，∴＝＝，∵⊙O半徑為8，∴OB＝8，∴AD＝4，∴AC＝＝4，∵OB⊥AC，∴AE＝CE＝2，∵OE＝AD＝2，∴BE＝6，∴BC

7、＝＝4. 15．如圖，△ABC內(nèi)接于⊙O，AB＝AC，CO的延長線交AB于點D． (1)求證：AO平分∠BAC； (2)若BC＝6，sin∠BAC＝，求AC和CD的長． (1)證明：如圖，延長AO交BC于H，連接OB，∵AC＝AB，OC＝OB，∴A，O在線段CB的中垂線上，∴OA⊥CB，∵AC＝AB，∴AO平分∠BAC； (2)解：如圖，過點D作DK⊥AO于K. ∵由(1)知OC＝OB，AO⊥BC，BC＝6，∴BH＝CH＝BC＝3，∠COH＝∠BOC，∵∠BAC＝∠BOC，∴∠COH＝∠BAC，在Rt△COH中，∵∠OHC＝90°，sin∠COH＝，CH＝3，∴sin∠COH＝＝，∴CO＝AO＝5，∴OH＝＝＝4，∴AH＝AO＋OH＝4＋5＝9，tan∠COH＝tan∠DOK＝，在Rt△ACH中，∠AHC＝90°，AH＝9，CH＝3， ∴tan∠CAH＝＝，AC＝＝＝3①，由(1)知∠CAH＝∠BAH，∴tan∠CAH＝tan∠BAH＝，設(shè)DK＝3a，在Rt△ADK中，tan∠BAH＝，在Rt△DOK中，tan∠DOK＝，OK＝4a，OD＝5a，AK＝9a，∴AO＝OK＋AK＝13a＝5，∴a＝，OD＝5a＝，CD＝OC＋OD＝5＋＝②.∴AC＝3，CD＝. 5