《安徽省2019年中考數(shù)學總復(fù)習 第六章 圓 第一節(jié) 圓的基本性質(zhì)練習》由會員分享,可在線閱讀�����,更多相關(guān)《安徽省2019年中考數(shù)學總復(fù)習 第六章 圓 第一節(jié) 圓的基本性質(zhì)練習(6頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
1、
第六章 圓
第一節(jié) 圓的基本性質(zhì)
姓名:________ 班級:________ 限時:______分鐘
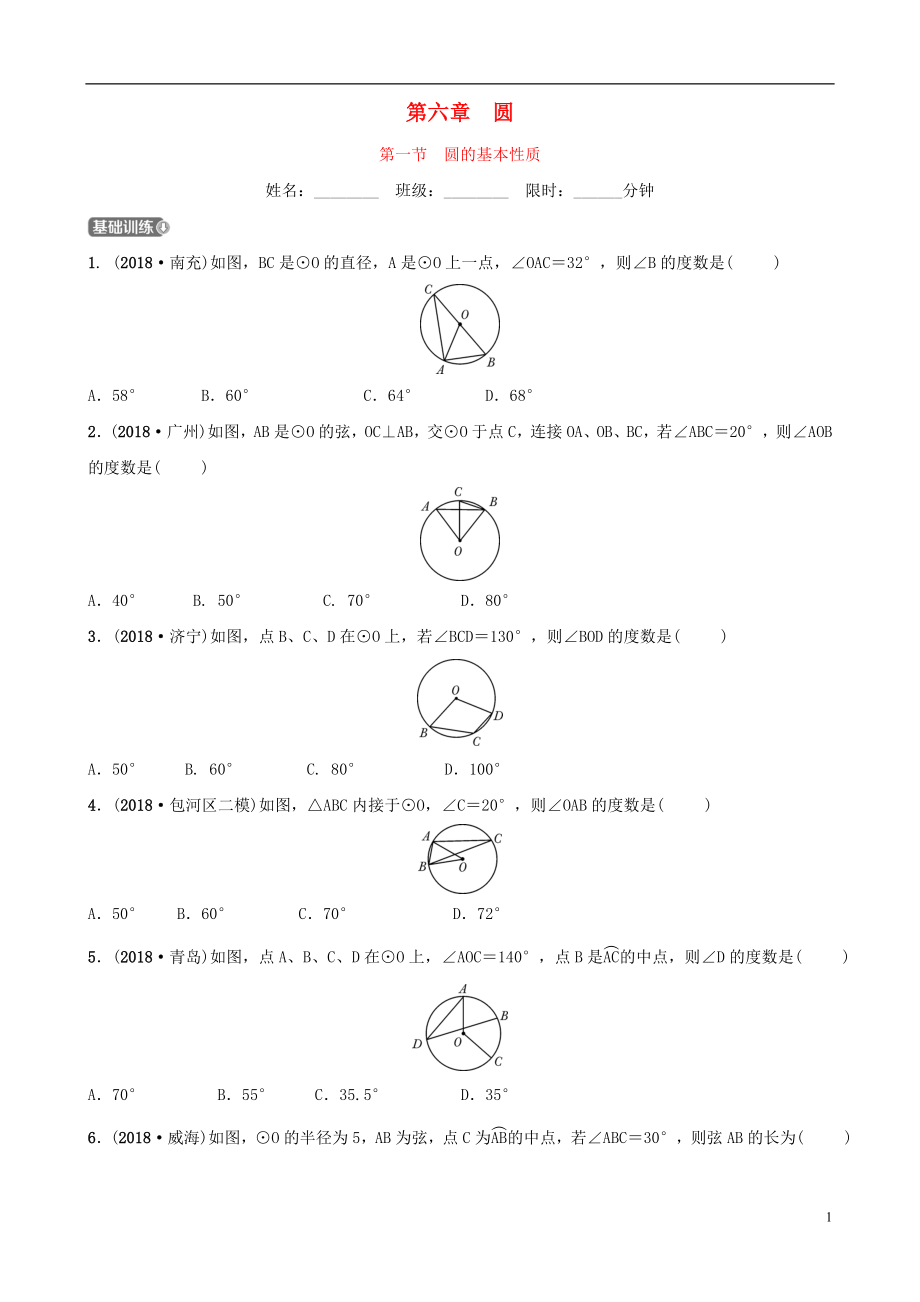
1. (2018·南充)如圖����,BC是⊙O的直徑��,A是⊙O上一點�����,∠OAC=32°�,則∠B的度數(shù)是( )
A.58° B.60° C.64° D.68°
2.(2018·廣州)如圖,AB是⊙O的弦��,OC⊥AB����,交⊙O于點C,連接OA、OB�、BC,若∠ABC=20°����,則∠AOB的度數(shù)是( )
A.40° B. 50° C. 70° D.80°
3.(2018·濟寧)如圖,點B�����、C�、D
2、在⊙O上�����,若∠BCD=130°���,則∠BOD的度數(shù)是( )
A.50° B. 60° C. 80° D.100°
4.(2018·包河區(qū)二模)如圖����,△ABC內(nèi)接于⊙O�,∠C=20°,則∠OAB的度數(shù)是( )
A.50° B.60° C.70° D.72°
5.(2018·青島)如圖�����,點A、B�����、C����、D在⊙O上,∠AOC=140°���,點B是的中點���,則∠D的度數(shù)是( )
A.70° B.55° C.35.5° D.35°
6.(2018·威海
3����、)如圖,⊙O的半徑為5���,AB為弦���,點C為的中點�����,若∠ABC=30°���,則弦AB的長為( )
A. B.5 C. D.5
7.(2018·瑤海區(qū)二模)如圖,A�、B、C�、D四個點均在⊙O上,∠AOD=50°�����,AO∥OC�,則∠B的度數(shù)為( )
A.50° B.55° C.60° D.65°
8.(2018·邵陽)如圖所示,四邊形ABCD為⊙O的內(nèi)接四邊形��,∠BCD=120°����,則∠BOD的大小是( )
A.80° B.120° C.100° D.90°
9.(2018·襄陽)如圖,點A
4����、�、B��、C�����、D都在半徑為2的⊙O上�����,若OA⊥BC�,∠CDA=30°,則弦BC的長為( )
A.4 B.2 C. D.2
10.(2018·棗莊)如圖���,AB是⊙O的直徑����,弦CD交AB于點P���,AP=2,BP=6, ∠APC=30°���,則CD的長為( )
A. B.2 C.2 D.8
11.(2018·隨州)如圖���,點A�����、B���、C在⊙上,∠A=40°�����,∠C=20°���,則∠B=__________.
12.(2018·廣東)同圓中���,已知弧AB所對的圓心角是100°,則弧AB所對的圓周角是________
5���、__.
13.(2018·南通)如圖��,AB是⊙O的直徑�����,點C是⊙O上一點����,若BC=3,AB=5�,OD⊥BC于點D,則OD的長為______.
14.(2019·原創(chuàng))如圖�����,A��、B����、C、D是⊙O上四點���,BD是⊙O的直徑.若四邊形ABCO是平行四邊形���,則∠ADB=__________.
15.(2018·杭州)如圖,AB是⊙O的直徑����,點C是半徑OA的中點,過點C作DE⊥AB����,交⊙O于D、E兩點����,過點D作直徑DF,連接AF�,則∠DFA=__________.
16.(2018·內(nèi)江)已知△ABC的三邊a、b��、c滿足a+b2+|c-6|+28=4+10b�,則△ABC的外接圓半徑=_
6、_______.
17.(2019·原創(chuàng))如圖���,AB是圓O的直徑�����,CD是圓O的弦����,且CD⊥AB于點E.
(1)求證:∠BCO=∠D;
(2)若CD=8����,AE=3,求圓O的半徑.
18.(2019·原創(chuàng))如圖����,線段AB是⊙O的直徑,弦CD⊥AB于點H����,P是 上任意一點,AH=2�����,CH=4.
(1)求⊙O的半徑r的長度�����;
(2)求sin ∠CPD.
1.(2018·安順)已知⊙O的直徑CD=10 cm����,AB是⊙O的弦,AB⊥CD�,垂足為M,且AB=8 cm,
7�����、則AC的長為( )
A. 2 cm B. 4 cm
C.2cm或4cm D.2 cm或4 cm
2.(2019·原創(chuàng)) 如圖�����,△ABC內(nèi)接于⊙O��,∠ACB=90°�����,∠ACB的平分線交⊙O于D�����,若AC=6�,BD=5���,則tan∠ABC=________.
3.(2018·嘉興)如圖���,量角器的0度刻度線為AB. 將一矩形直尺與量角器部分重疊,使直尺一邊與量角器相切于點C,直尺另一邊交量角器于點A���、D�,量得AD=10 cm�����,點D在量角器上的讀數(shù)為60°.則該直尺的寬度為________cm.
4. (2019·原創(chuàng))如圖����,四邊形ABC
8、D是⊙O的內(nèi)接四邊形�����,延長BC��,AD交于點E���,且CE=AB=AC�,連接BD���,交AC于點F.
(1)證明:BD平分∠ABC����;
(2)若AD=6,BD=8��,求DF的長.
參考答案
【基礎(chǔ)訓練】
1.A 2.D 3.D 4.C 5.D 6.D 7.D 8.B 9.D 10.C
11.60° 12.50° 13.2 14.30° 15.30° 16.
17.(1)證明:OB=OC���,∴∠OBC=∠OCB,
∵∠ADC=∠ABC��,∴∠BCO=∠D.
(2)解:∵OA⊥CD��,∴CE=DE=4���,
設(shè)圓O的半徑為r��,則OE=OA-AE=r-3����,
在Rt△OCE中�,由
9、勾股定理得OC2=CE2+OE2�����,
即r2=42+(r-3)2,
解得r=.
18.解:(1)如解圖��,連接OC�,
∵AB⊥CD,∴∠CHO=90°�����,
在Rt△COH中����,∵OC=r,OH=r-2�,CH=4,
∴r2=42+(r-2)2�����,∴r=5�;
(2)如解圖,連接OD.
∵AB⊥CD�����,AB是直徑���,
∴==�,∴∠AOC=∠COD.
∵∠CPD=∠COD,∴∠CPD=∠COA.
在Rt△OCH中����,sin ∠COA==.
∴sin ∠CPD=sin ∠COA=.
【拔高訓練】
1.C 2. 3.
4.(1)證明:∵CE=AC,∴∠E=∠CAE��,
∵AB=AC��,∴∠ABC=∠ACB.
∵∠DBC=∠CAE���,∴∠DBC=∠E=∠CAE.
∴∠ABC-∠DBC=∠ACB-∠E,
∴∠ABD=∠CAE�,
∴∠ABD=∠DBC,即BD平分∠ABC.
(2)解:由(1)知��,∠CAE=∠DBC=∠ABD���,
又∵∠ADF=∠ADB���,∴△ADF∽△BDA,∴=�����,
∵AD=6,BD=8���,∴DF===.
6
 安徽省2019年中考數(shù)學總復(fù)習 第六章 圓 第一節(jié) 圓的基本性質(zhì)練習
安徽省2019年中考數(shù)學總復(fù)習 第六章 圓 第一節(jié) 圓的基本性質(zhì)練習