《山東省濱州市2019中考數(shù)學 第四章 幾何初步與三角形 第七節(jié) 相似三角形要題隨堂演練》由會員分享，可在線閱讀，更多相關《山東省濱州市2019中考數(shù)學 第四章 幾何初步與三角形 第七節(jié) 相似三角形要題隨堂演練（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

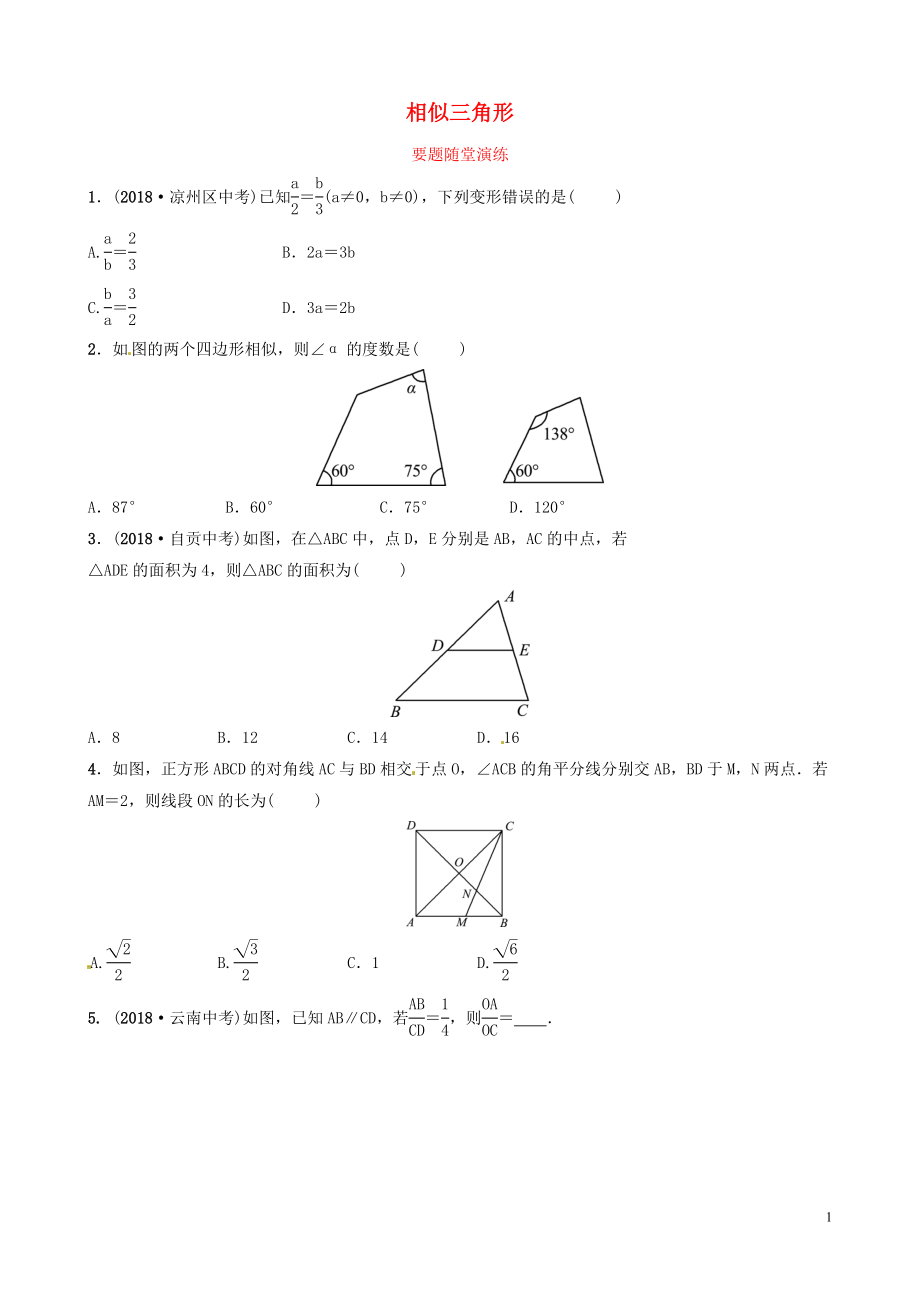
1、相似三角形 要題隨堂演練 1．(2018·涼州區(qū)中考)已知＝(a≠0，b≠0)，下列變形錯誤的是( ) A.＝ B．2a＝3b C.＝ D．3a＝2b 2．如圖的兩個四邊形相似，則∠α的度數(shù)是( ) A．87° B．60° C．75° D．120° 3．(2018·自貢中考)如圖，在△ABC中，點D，E分別是AB，AC的中點，若 △ADE的面積為4，則△ABC的面積為( ) A．8 B．12 C．14 D．16 4．如圖，正方形ABCD的對角線AC與BD相交于點O，∠ACB的角平分

2、線分別交AB，BD于M，N兩點．若AM＝2，則線段ON的長為( ) A. B. C．1 D. 5. (2018·云南中考)如圖，已知AB∥CD，若＝，則＝ ． 6．如圖，D，E分別是△ABC的邊AB，BC上的點，且DE∥AC，AE，CD相交于點O，若S△DOE∶S△COA＝1∶16，則S△BDE與S△CDE的比是 ． 7．(2018·泰安中考)如圖，在菱形ABCD中，AC與BD交于點O，E是BD上一點，EF∥AB，∠EAB＝∠EBA，過點B作DA的垂線，交DA的延長線于點G. (1)∠DEF和∠AEF是否相等？若相等，請證明；若

3、不相等，請說明理由； (2)找出圖中與△AGB相似的三角形，并證明； (3)BF的延長線交CD的延長線于點H，交AC于點M.求證：BM2＝MF·MH. 參考答案 1．B　2.A　3.D　4.C　5.　6.1∶3 7．解：(1)∠DEF＝∠AEF.理由如下： ∵EF∥AB，∴∠DEF＝∠EBA，∠AEF＝∠EAB. 又∵∠EAB＝∠EBA，∴∠DEF＝∠AEF. (2)△EOA∽△AGB，證明如下： ∵四邊形ABCD是菱形，∴AB＝AD，AC⊥BD， ∴∠GAB＝∠ABE＋∠ADB＝2∠ABE. 又∵∠AEO＝∠ABE＋∠BAE＝2∠ABE， ∴∠GAB＝∠AEO. 又∵∠AGB＝∠AOE＝90°，∴△EOA∽△AGB. (3)如圖，連接DM. ∵四邊形ABCD是菱形，由對稱性可知BM＝DM， ∠ADM＝∠ABM. ∵AB∥CH， ∴∠ABM＝∠H， ∴∠ADM＝∠H. 又∵∠DMH＝∠FMD， ∴△MFD∽△MDH， ∴＝， ∴DM2＝MF·MH， ∴BM2＝MF·MH. 3