《重慶市2018年中考數(shù)學題型復習 題型七 幾何圖形的相關證明及計算 類型四 構造等腰三角形練習》由會員分享，可在線閱讀，更多相關《重慶市2018年中考數(shù)學題型復習 題型七 幾何圖形的相關證明及計算 類型四 構造等腰三角形練習（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。

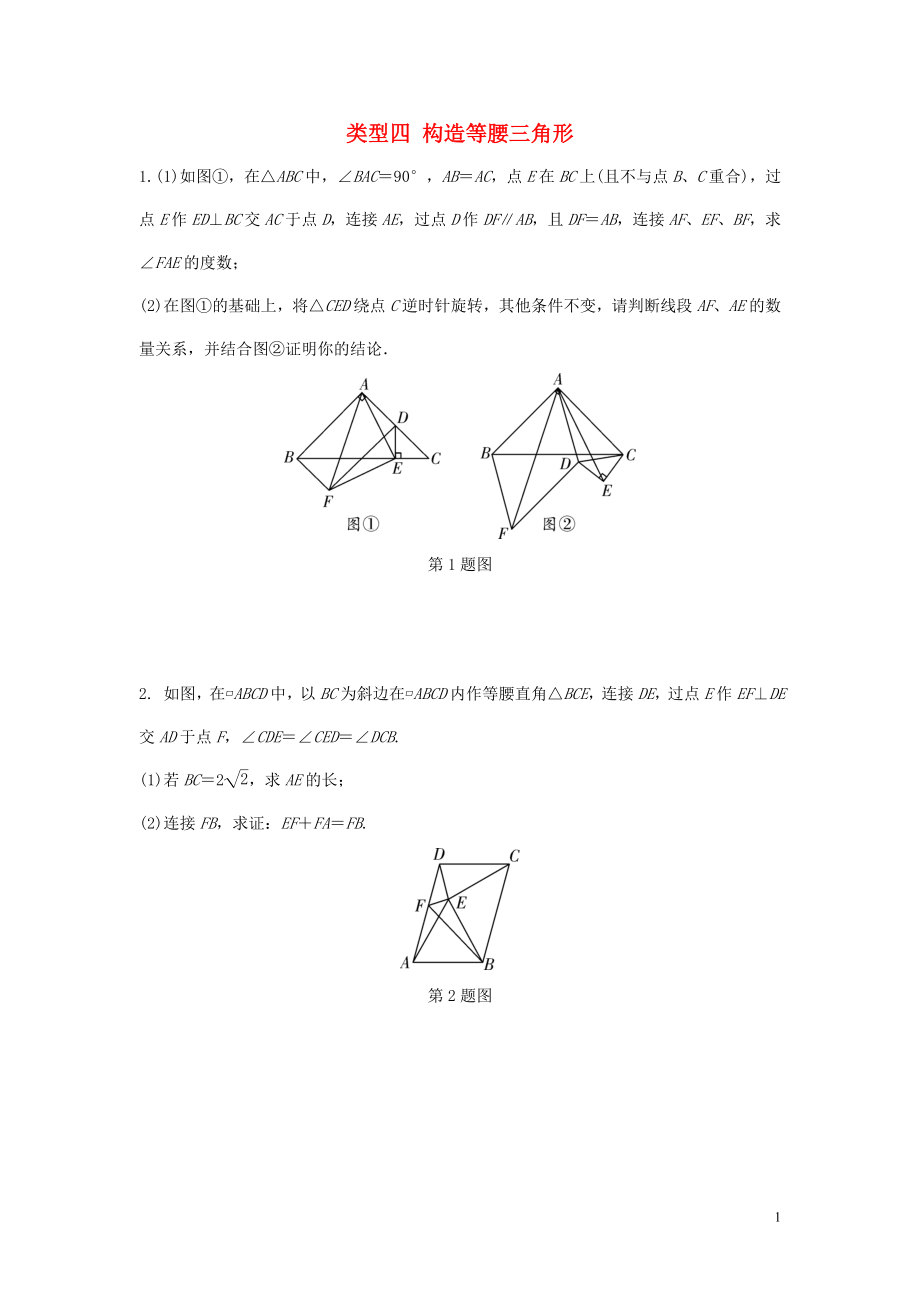
1、 類型四 構造等腰三角形 1. (1)如圖①，在△ABC中，∠BAC＝90°，AB＝AC，點E在BC上(且不與點B、C重合)，過點E作ED⊥BC交AC于點D，連接AE，過點D作DF∥AB，且DF＝AB，連接AF、EF、BF，求∠FAE的度數(shù)； (2)在圖①的基礎上，將△CED繞點C逆時針旋轉，其他條件不變，請判斷線段AF、AE的數(shù)量關系，并結合圖②證明你的結論． 第1題圖 2. 如圖，在?ABCD中，以BC為斜邊在?ABCD內(nèi)作等腰直角△BCE，連接DE，過點E作EF⊥DE交AD于點F，∠CDE＝∠CED＝∠DCB. (1)若BC＝2，求AE的長； (2)連接FB，求

2、證：EF＋FA＝FB. 第2題圖 答案 1. 解：(1)∵DF∥AB，∠BAC＝90°，AB＝AC， ∴∠FDC＝90°，∠EDC＝∠C＝45°， ∴DE＝EC， ∴∠FDE＝∠C＝45°. ∵AC＝AB，DF＝AB， ∴AC＝DF， ∴△AEC≌△FED(SAS)， ∴EF＝EA，∠AEC＝∠FED， ∴∠FED－∠AED＝∠AEC－∠AED， ∴∠FEA＝∠DEC＝90°， ∴△AEF是等腰直角三角形，∠FAE＝45°； (2)AF＝AE. 證明：如解圖，連接EF，延長FD交AC于點K， ∵DF∥AB, ∠BAC＝90°， ∴∠FKC＝

3、90°. ∵∠EDF＝180°－∠KDC－∠EDC＝135°－∠KDC，∠ECA＝90°－∠KDC＋ ∠DCE ＝135°－∠KDC， ∴∠EDF＝∠ECA， ∵DF＝AB，AB＝AC, ∴DF＝AC， ∴△EDF≌△ECA(SAS)， ∴EF＝EA，∠FED＝∠AEC， ∴∠FEA＝∠DEC＝90°， ∴△AEF是等腰直角三角形， ∴AF＝AE. 第1題解圖 2. (1)解：設∠CDE＝∠CED＝∠DCB＝α， ∵在等腰直角△BCE中，BC＝2， ∴∠DCE＝α－45°，BE＝2， ∴2α＋α－45°＝180°， ∴α＝75°， ∵四邊形ABCD是平行

4、四邊形， ∴AB＝CD＝BE, ∠DCB＋∠CBA＝180°， ∴∠CBA＝105°. ∵∠CBE＝45°， ∴∠EBA＝60°， ∴△ABE為等邊三角形， ∴AE＝2； (2)證明：如解圖，延長FA至點H，使AH＝FE，連接BH. ∵FE⊥DE，CE⊥EB, ∠DEC＝75°， ∴∠FEB＝105°. ∵四邊形ABCD是平行四邊形， ∴∠DAB＝75°， ∴∠HAB＝∠FEB， 又∵AB＝BE，AH＝FE， ∴△FEB≌△HAB(SAS)， ∴FB＝HB，∠FBE＝∠HBA， ∵∠ABE＝60°，∴∠FBH＝60°， ∴△FBH為等邊三角形， ∴FB＝FH＝FA＋AH＝FA＋EF. 第2題解圖 4